Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 160

Determine o módulo da seção plástica e o fator de forma da seção transversal da viga.

Passo 1

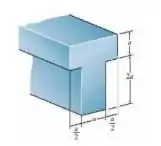
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa viga tem uma altura a para o topo do T e 2a para a base compridona dele. Então, precisamos encontrar o módulo e o fator de forma. Partiu??

Passo 2

Ok, nós vamos começar pensando na barra. Ela é em formato de T e tem uma linha neutra posicionada em:

y =   ∑ A y ∑ A =   2 a   x   a a + 2 a   x   a ( 2,5 a ) 2 a   x   a + ( 2 a   x   a ) = 1,75 a

Feito isso, vamos achar a distância d através das nossas forças de contração, sendo elas:

C 1 (mais para o centro) C 2 (mais na borda)

Sabendo disso, vamos calcular nosso C1 inicial.

C 1 = ( 0,5   h -   y e )   .   σ e   .   b   C 1 = 2 a - d a σ e

Agora, vamos calcular nosso C2.

C 2 = 0,5   y e   .   σ e   .   b   C 2 = 2 a ² σ e  

Sabendo que a soma das duas é igual a a d σ e , achamos que:

d = 2 a ² σ e

Passo 3

Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos o nosso momento.

M p = C 1 . d 1 + C 2 . d 2 = 3 a ³ σ e

Com o nosso momento achado, vamos descobrir a nossa tensão máxima em função do nosso momento elástico.

σ e =   M e . c I =   M e   x   1,75 a a 2 a 3 12 + 2 a   x   a   x   0,75 a 2 + 2 a   x   a 3 12 + 2 a   x   a   x   0,75 a 2 M e = 1,762   a ³   σ e

Finalmente, podemos botar nas fórmulas do módulo da seção plásticas e do fator da seção transversal.

k =   M p M e = 1,7 Z =   M p σ e = 3 a ³

Resposta

k =   1,7 Z =   3 a ³

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra tem espessura de 12,5 mm e está sujeita a um momento de 90 N.m. Determine a tensão de flexão máxima na barra.
Determine o comprimento L da porção da barra de modo que as tensões de flexão máximas em A, B e C sejam as mesmas. A barra tem espessura de 10 mm.
Determine a tensão de flexão máxima desenvolvida na barra se ela for submetida aos conjugados mostrados na figura. A barra tem espessura de 6 mm.
Uma barra retangular de aço A-36 tem largura 25 mm e altura 75 mm. Determine o momento aplicado em torno do eixo horizontal que provocará o escoamento de metade da barra, considerando σe = 250 MPa.
A viga é feita de um material elástico perfeitamente plástico. Determine o momento elástico máximo e o momento plástico que podem ser aplicados à seção transversal. Considere a = 50 mm e σe = 230 MPa.