Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 219
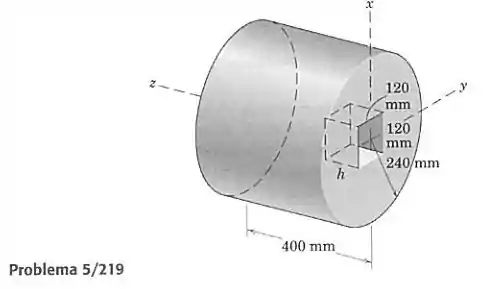
Determine a profundidade de um furo quadrado no cilindro circular sólido, para o qual a coordenada do centro de massa terá o máximo valor possível..
Passo 1
Se combinarmos o cilindro completo de volume com o furo, sendo o volume do furo considerado negativo, conseguimos calcular a coordenada do centro de massa com a seguinte fórmula:
Sendo e o volume e coordenada do CM do cilindro completo sem o furo, e e o volume e coordenada do centro de massa do furo. Devemos então encontrar em função da profundidade do furo, e então maximizar a função para o intervalo .
Passo 2
Como o cilindro tem raio 240 mm e altura de 400 mm, seu volume é dado por:
A coordenada do centro de massa será a metade de sua altura:
Passo 3
O furo tem volume dado por:
Seu centro de massa também fica na metade de sua profundidade:
Passo 4
Agora vamos aplicar a fórmula, com os volumes e coordenadas calculados:
Vamos simplificar dividindo em cima e em baixo por 1440:
Mais uma vez, agora por 5:
Passo 5
Para encontrarmos o ponto de coordenada máxima, devemos derivar a função:
Como o denominador é sempre positivo para entre 0 e 400 mm, vamos ter um ponto crítico quando . Então:
Vamos resolver a equação para :
O resultado que temos no intervalo que queremos é:
Que faz com que a coordenada do centro de massa seja:
Como esse é o único ponto crítico no intervalo e nos extremos temos , pois temos um corpo simétrico, temos de fato o valor máximo absoluto para .