Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 41

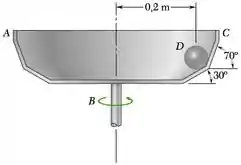
Uma esfera D de 100 g está em repouso em relação a um tambor que gira a uma taxa constante. Desprezando o atrito, determine o intervalo admissível da velocidade v da esfera se nenhuma das forças exercidas pela esfera na superfície inclinada do tambor deve exceder 1,1 N.

Passo 1

O enunciado pede que a gente encontre o intervalo admissível da velocidade v da esfera se nenhuma das forças exercidas pela esfera na superfície inclinada do tambor deve exceder 1,1 N.

Primeiro notamos

a D = a n = v D 2 ρ

onde

ρ = 0.2   m

← + Σ F x = m D a D :         N 1 cos ⁡ 60 ° + N 2 cos ⁡ 20 ° = m D v D 2 ρ

+ ↑ Σ F y = 0 :       N 1 sin ⁡ 60 ° + N 2 sin ⁡ 20 ° - w D = 0

ou

N 1 sin ⁡ 60 ° + N 2 sin ⁡ 20 ° = m D g

Passo 2

Caso 1: N1 é máximo.

Seja

N 1 = 1.1   N

Eq (2)

1.1   N sin ⁡ 60 ° + N 2 sin ⁡ 20 ° = 0.1   kg 9.81   m/ s 2

ou

N 2 = 0.082954   N

( N 2 ) ( N 1 ) max < 1.1   N.    O.K.

Eq. (1)

( v D 2 ) ( N 1 ) max = 0.2   m 0.1   kg 1.1 cos ⁡ 60 ° + 0.082954 cos ⁡ 20 °   N

ou

( v D ) ( N 1 ) max = 1.121   m/s

Agora nós formamos

sin ⁡ 20 ° 1 - cos ⁡ 20 ° 2

N 1 cos ⁡ 60 ° sin ⁡ 20 ° - N 1 sin ⁡ 60 ° cos ⁡ 20 ° = m D v D 2 ρ sin ⁡ 20 ° - m D g cos ⁡ 20 °

ou

- N 1 sin ⁡ 40 ° = m D v D 2 ρ sin ⁡ 20 ° - m D g cos ⁡ 20 °

( v D ) min   ocorre quando   N 1 = ( N 1 ) max

( v D ) min   = 1.121   m/s

Passo 3

Caso 2: N2 é máximo.

Seja

N 2 = 1.1   N

Eq (2)

N 1 sin ⁡ 60 ° + 1.1   N sin ⁡ 20 ° =   ⁡ 0.1   kg 9.81   m/ s 2

N 1 = 0.69834   N

( N 1 ) ( N 2 ) max < 1.1   N.    O.K.

Eq. (1)

( v D 2 ) ( N 2 ) max = 0.2   m 0.1   kg 0.69834 cos ⁡ 60 ° + 1.1 cos ⁡ 20 °   N

ou

( v D ) ( N 2 ) max = 1.663   m/s

Agora nós formamos

sin ⁡ 60 ° 1 - cos ⁡ 60 ° 2

N 2 cos ⁡ 20 ° sin ⁡ 60 ° - N 2 sin ⁡ 20 ° cos ⁡ 60 ° = m D v D 2 ρ sin ⁡ 60 ° - m D g cos ⁡ 60 °

ou

N 2 cos ⁡ 40 ° = m D v D 2 ρ sin ⁡ 60 ° - m D g cos ⁡ 60 °

( v D ) max   ocorre quando   N 2 = ( N 2 ) max

( v D ) max   = 1.663   m/s

Para  N 1 , N 2 ≤ 1.1   N

Resposta

1.121   m/s ≤ v D ≤ 1.663   m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois carros, A e B , têm massas de 2M g e 1,5M g , respectivamente. Determine as intensidades de v A e v B se os carros colidem e aderem um ao outro, enquanto movem-se a uma velocidade comum de 50k m
O garoto de 75k g salta do carrinho A , a uma velocidade horizontal v ' = 3m / s , medida relativamente ao carrinho. Determine a velocidade do carrinho A logo após o salto. Se o garoto então atinge o
O pacote de 40k g é jogado a uma velocidade de 4m / s sobre o carrinho, que tem massa de 20k g . Se o pacote desliza sobre a superfície lisa e atinge a mola, determine a velocidade do carrinho no inst
O carro A tem massa de 2250k g e está viajando para a direita a 1m / s . Enquanto isso, um carro B , de 1500k g , está viajando para esquerda a 2m / s . Se os carros colidem de frente e emaranham-se,
A bala de canhão de 5k g é disparada horizontalmente por um canhão de 250k g , como mostra a figura. Se a velocidade de saída da bala é 600m / s , medida relativamente ao solo, determine a velocidade