Exercícios de Impulso e Quantidade de Movimento Linear - Lista de Exercícios Resolvida
Questão 1
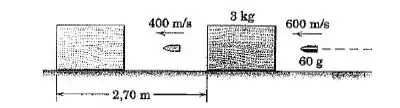
Uma bala de é disparada horizontalmente com uma velocidade contra o bloco de de madeira macia inicialemnte em repouso sobre a superfície horizontal. A bala emerge do bloco com a velocidade , e se observa que o bloco desliza uma distância de antes de parar. Determine o coeficiente de atrito dinâmico entre o bloco e a superfície.
Questão 2
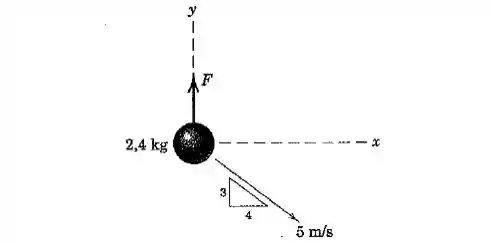
A partícula de se desloca no plano horizontal xy e tem a velocidade mostrada no instante de tempo . Se a força newtons, onde é o tempo em segundos, é aplicada à partícula na direção y iniciando no instante de tempo , determine a velocidade da partícula 4 segundos após ser aplicada e especifique o ângulo correspondente medido no sentido anti-horário a partir do eixo x até a direção da velocidade.
Questão 3
O motor de foguete de uma nave espacial com se deslocando a uma velocidade de é acionado e produz um empuxo de na direção de sua trajetória circular durante um período de . Determine a nova velocidade da nave espacial. A perda de massa devida ao combustível queimado é desprezivelmente pequena.
Ver solução completaQuestão 4
Um projétil de viajando a atinge e se incorpora ao bloco de , que está inicialmente parado. Calcule a energia perdida durante o impacto. Expresse sua resposta como um valor absoluto e como uma percentagem da energia original do sistema .

Questão 5
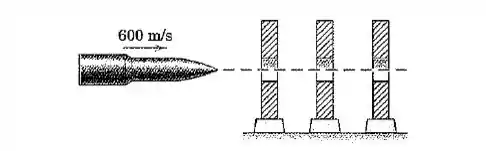
O projétil de é disparado com uma velocidade de e carrega três anilhas, cada uma com uma massa de . Encontre a velocidade comum do projétil e das anilhas. Determine também a perda de energia durante a interação.
Questão 6
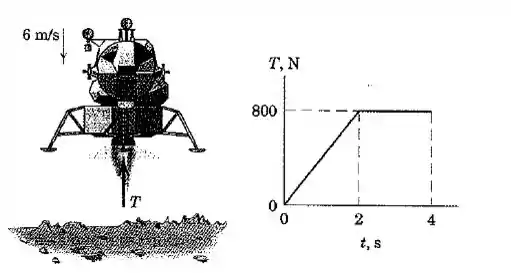
O módulo de aterrissagem lunar de está descendo na superfície da Lua com uma velocidade de quando seu retromotor é acionado. Se o motor produz um empuxo por que varia com o tempo como mostrado e em seguida desliga, calcule a velocidade do módulo de aterrissagem quando , supondo que ele ainda não aterrisou. A aceleração gravitacional na superfície da Lua é .
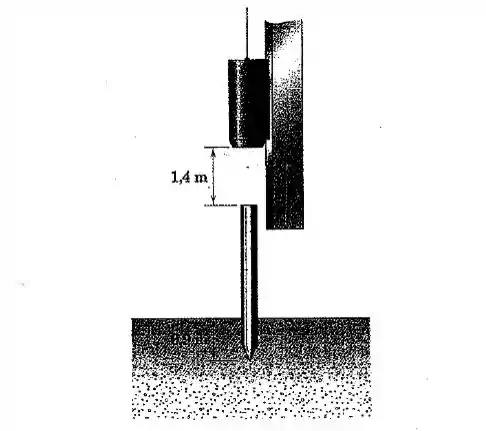
Questão 7
O martelo com de um bate-estaca cai a partir do repouso e atinge o topo de uma estaca de enterrada no solo. Após o impacto observa-se o martelo se deslocar com a estaca sem ricochetear visivelmente. Determine a velocidade da estaca e do martelo imediatamente após o impacto. Você pode justificar o uso do princípio da conservação da quantidade de moviemnto embora os pesos atuem durante o impacto?