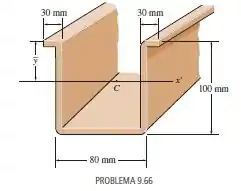
Uma estrutura de alumínio possui uma seção transversal conhecida como “chapéu fundo”. Localize o centroide de sua área. Cada segmento tem uma espessura de .
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Nesse problema temos uma estrutura homogênea de alumínio e nosso objetivo é calcular seu centroide na coordenada sendo que cada seguimento tem de espessura.
Lembra como fazemos isso?
O centroide de uma área em é dada por:
Ou, nesse caso, podemos separar a área total do objeto como:
Em que é o centro da -ésima parte.
Bora lá!
Passo 2
Vamos começar redesenhando a área do objeto:
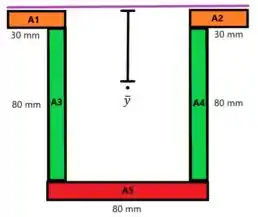
Assim, podemos escrever o somatório como:
Porém, perceba que , e , ou seja:
Tranquilo até aqui?
Passo 3
Agora vamos calcular cada ...
Lembrando que nossa referência é a parte superior do objeto, a linha roxa.
Para , temos:
Para , temos
E para , temos:
Substituindo tudo isso em , chegamos em:
É isso! O que achou? Responde Aí!