Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 24
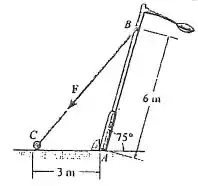
A fim de erguer o poste de iluminação a partir da posição mostrada, a força é aplicada ao cabo. Se , determine o momento produzido por em relação ao ponto .
Passo 1
Oi, galerinha! Tudo bom? O momento gerado pela força pode ser determinado através de suas componentes e aplicando o princípio dos momentos. Para isso, vamos lembrar que o momento é dado por:
Como isso é um produto vetorial, se deixarmos os vetores numa forma escalar, podemos reescrever a equação como:
Onde é a distância do ponto de referência até o local de ação da força e é o ângulo entre a força e a distância .
Para enxergar bem todas essas informações, vamos fazer o diagrama de corpo livre do poste:
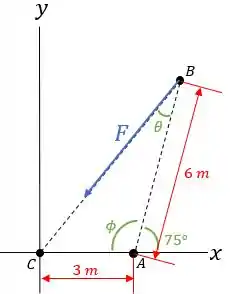
Então primeiro vamos encontrar o ângulo , para depois acharmos o momento.
Passo 2
Dessa forma, o comprimento pode ser determinado usando a lei dos cossenos que, nesse caso, é dada por:
E substituindo o valor de cada variável:
Assim, podemos aplicar a lei dos senos para encontrar . Logo:
Passo 3
A partir disso, o momento em relação ao ponto pode ser encontrado. Supondo que o momento positivo seja dado no sentido anti-horário:
Então:
Portanto:
Como o resultado é positivo, o momento estará agindo no sentido anti-horário.
Resposta
O momento produzido por em relação ao ponto é dado por: