Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 59

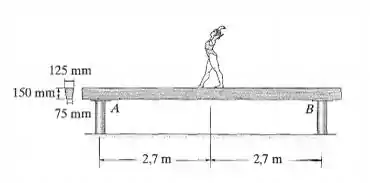
Uma ginasta de 60 kg está em pé no centro da trave (viga) de equilíbrio simplesmente apoiada. Se a trave for feita de madeira e tiver a seção transversal mostrada na figura, determine a deflexão máxima. Considere que os apoios em A e B são rígidos. Em = 12 GPa.

Passo 1

Podemos de cara montar a equação do momento. Ela será dada por:

M x = 294,3 x - 588,6 < x - 2,7 >

Sabemos que:

E I d 2 v d x 2 = M x =   294,3 x - 588,6 < x - 2,7 >

Logo, integrando-se os 2 lados 2 vezes, temos:

E I v = 49,05 x ³ - 98,1 < x - 2,7 > ³ + C 1 x + C 2

Passo 2

As condições de contorno serão:

x = 0 → v = 0

x = 5,4 → v = 0

Logo:

C 1 = - 1072,7235

C 2 = 0

O próximo passo é calcular a coordenada y do centróide:

y = 150 × 75 75 + 2 25 × 150 0,5 100 150 × 75 + 2 25 × 150 0,5 = 81,25 m m

O momento de inércia será:

I = 0,075 × 0,15 3 12 + 0,075 × 0,15 × 0,00625 2 + 2 0,025 × 0,15 3 36 + 0,025 × 0,15 2 × 0,01875 2 = 2,75390625 × 10 - 5  

Portanto, podemos calcular a deflexão:

∆ m á x = 49,05 × 2,7 3 - 1072,7235 × 2,7 12 × 10 9 2,75390625 × 10 - 5 = - 0,00584 m

Resposta

∆ m á x = - 0,00584 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar:A deflexão no ponto médio C.
A barra rígida D E C é soldada no ponto C ao perfil laminado de aço A B . Para o carregamento mostrado, determinar:A deflexão no ponto C
A barra rígida D E C é soldada no ponto C ao perfil laminado de aço A B . Para o carregamento mostrado, determinar:A deflexão no ponto C
A barra rígida D E C é soldada no ponto C ao perfil laminado de aço A B . Para o carregamento mostrado, determinar:A declividade no ponto A
A barra rígida D E C é soldada no ponto C ao perfil laminado de aço A B . Para o carregamento mostrado, determinar:A declividade no ponto A