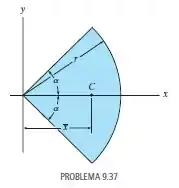
Localize o centroide do setor circular.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Nesse problema temos uma figura de um setor circular e nosso objetivo é encontrar seu centroide .
Tem ideia de como fazemos isso?
Para resolver esse problema temos que aplicar a formulinha
Bora começar!
Passo 2
Podemos considerar que esse setor circular é formado por triângulos infinitesimais dessa forma:
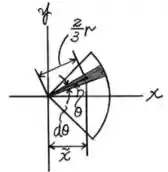
Dessa forma, podemos definir como:
Já podemos definir como
Dessa forma, a fórmula de fica assim:
Pela figura, vemos que está definida entre e , logo
Calculando as integrais, chegamos em:
E finalmente, encontramos que:
É isso! Entendeu tudo? Responde Aí!