Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 80
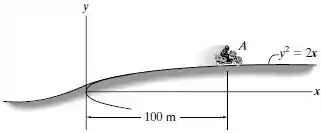
Uma moto de 800 kg se move com velocidade constante de 80 km/h morro acima. Determine qual é a força normal que a superfície exerce sobre as suas rodas quando ela chega ao ponto . Despreze a sua dimensão.
Passo 1
O enunciado nos dá as seguintes informações:
Massa da moto: 800 kg;
Trajetória curva: ;
Velocidade constante: km/h m/s
Posição do ponto : m
Nosso objetivo é determinar a força normal quando a moto chega no ponto.
Primeiramente, desenharemos o Diagrama de Corpo Livre da moto.
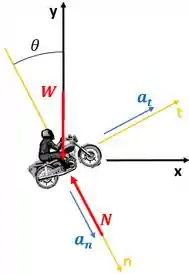
Onde = força peso
= força normal resultante
= aceleração tangencial
=aceleração normal
Lembre-se que a aceleração normal deve apontar no sentido positivo do eixo normal . Como a aceleração tangencial é desconhecida, vamos supor que ela atue na direção de positiva.
Sabemos que m/s2 e que
Onde é o raio de curvatura no ponto onde o corpo está localizado.
Passo 2
Fazendo uma análise da geometria da situação, temos que
Portanto, para o ponto m
Passo 3
Em seguida, devemos encontrar o ângulo .
Olhando novamente o diagrama de corpo livre, podemos ver que
Para o ponto m
Passo 4
Agora utilizaremos a Equação do movimento para encontrar a força no ponto .