Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 88
O carrinho de montanha-russa tem massa de 800 kg, incluindo seus passageiros. Se ele é solto do repouso no topo da estrutura A, determine a altura mínima h da estrutura de maneira que o carrinho dê a volta nos dois loops internos sem deixar os trilhos. Despreze o atrito, a massa das rodas e a dimensão do carrinho. Qual é a reação normal sobre o carrinho quando ele está em B e em C?
Passo 1
Com referência definida na figura representativa, para determinação da altura na posição A, faz-se necessário aplicar o princípio da conservação de energia entre os pontos (A) e (B).
As energias potenciais, exclusivamente gravitacionais, no caso, podem ser escritas através de:
A energia cinética para os dois pontos é expressa por:
Analisando os pontos em questão:
Ponto A: Origem do sistema.
- Pela referência definida, tem-se que a consequência imediata será =0.
- O carrinho parte do repouso no ponto A, i.e., =0 .
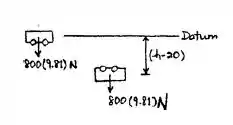
Em uma situação de imediata saída de A, o diagrama de corpo livre e a posição B nos fornecem as seguintes informações acerca do comportamento do fenômeno:
- A altura relativa ao ponto B, isto é, uma altura intermediária entre o ponto A e B é definida por, de acordo com a origem A:
- Na posição intermediária aos pontos A e B, nota-se uma trajetória curvilínea, satisfazendo a utilização adequada do sistema de coordenadas normal-tangencial, sendo assim, como não há forças no sentido tangencial, a análise será voltada completamente ao normal. Sabendo que o raio de curvatura da trajetória que engloba B é de 10 m, tem-se:
Passo 2
Identificadas as energias atuantes no sistema, admitindo que sejam conservativas, o princípio de conservação da energia mecânica será:
Substituindo as expressões no balanço energético, tem-se que:
Passo 3
Com as conclusões acerca dos pontos inicial e final da análise, a expressão de conservação de energia será:
Passo 4
Para que o carrinho execute os dois loops sem deixar os trilhos, a condição necessária para isso é que a Força normal seja nula, desse modo, caracterizando a pior condição para o problema, resultando na mínima altura h.
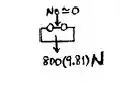
Então, para , realiza-se uma análise do ponto A ao ponto C, pelo princípio da conservação da energia mecânica, mantendo a origem em A:
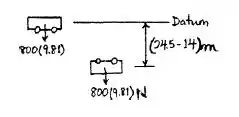
Substituindo as expressões no balanço energético, tem-se que:
Passo 5
Para determinar a força normal atuando em C, realizando a análise do sistema de coordenadas para a coordenada normal com sentido positivo para baixo e com = 7m , tem-se que:
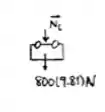
Resposta
Desse modo, para que o carrinho execute os dois loops e permaneça nos trilhos, é necessária que a altura mínima seja h = 25 m conjuntamente com = 9,904 m/s e = 14, 691 m/s. A força normal em C para manter a condição de não saída dos trilhos será de 16,817 kN.