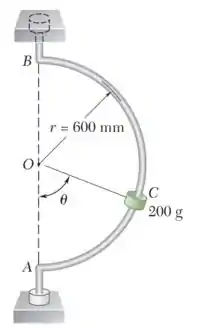
Um pequeno colar C de 200 g desliza em uma haste semicircular que é colocada para girar sobre a vertical AB a uma taxa constante de 6 rad/s. Determine o valor mínimo requerido do coeficiente de atrito estático entre o colar e a haste se o colar não desliza quando (a) , (b), (c) . Indique em cada caso a direção do movimento iminente.

(b) e (c)

Primeiro observe que para um valor arbitrário de , não se tem conhecimento se o movimento iminente será para cima ou para baixo. Para considerar as duas possibilidades para cada valor de , considere para movimento iminente para baixo, e corresponde ao movimente iminente para cima, então com o “sinal do topo” correspondendo a nós temos

Agora

Então

ou

Substituindo para N e F

ou

ou

Agora

Então

(b)

Então

Para baixo:

Para cima:

(c)

Então

Para baixo:

Para cima:

A direção do movimente iminente é para cima

Nota: Quando

ou

. Portanto, para esse valor de , fricção não necessariamente previne o colar de escorregar pela barra.