Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 6

Resolva o Problema 4.5 considerando que o caixote D foi removido e a posição do caixote C permanece inalterada.

Figura P4.5

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Precisamos determinar a reação em cada uma das rodas da caminhote, considerando que o caixote D foi removido, ou seja, desconsiderando o caixote D na Figura P4.5. Chamaremos a reação em cada uma das rodas traseiras de e a das rodas dianteiras de .

É apresentada a massa dos dois caixotes () e da caminhote (). Devemos calcular o peso dos caixotes e da caminhote, multiplicando suas massas pela aceleração da gravidade (). Dessa forma:

Agora temos todas as forças peso em N (Newtons) e todas as medidas estão em m (metros). Portanto, não será necessário converter unidades.

Passo 2

Agora podemos considerar o seguinte diagrama de corpo livre:

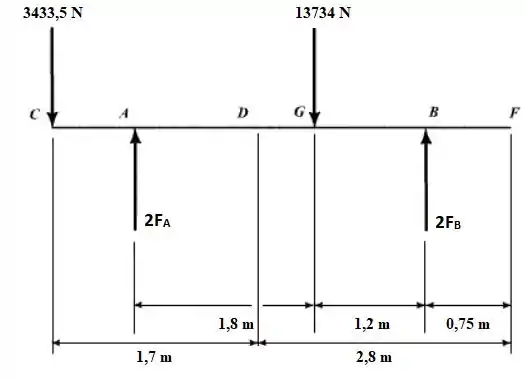
As forças nas posições A e B foram representadas com e pois em cada uma dessas posições horizontais temos duas rodas.

Analisando o diagrama podemos aplicar o somatório dos momentos em torno de B para determinar as reações em cada uma das rodas traseiras ():

indica a resultante em cada uma das rodas traseiras e o resultado positivo mostra que o sentido é o mesmo representado no diagrama de corpo livre, ou seja, para cima.

Passo 3

Uma vez determinadas as forças , faremos o somatório de forças verticais para determinar a força em cada uma das rodas dianteiras (). Temos que:

indica a resultante em cada uma das rodas dianteiras e o resultado positivo mostra que o sentido é o mesmo representado no diagrama de corpo livre, ou seja, para cima.