Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 16
Resolva o Problema 6.15 considerando que a carga aplicada em E foi removida.
Passo 1
Vamos começar o exercício desenhando o diagrama de corpo livre da treliça:
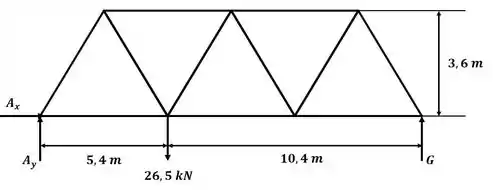
Agora aplicando o somatório de forças na direção :
Agora aplicando o somatório de momento com relação ao ponto G, temos:
E, aplicando o somatório de forças na direção :
Passo 2
Agora vamos analisar o nó A:
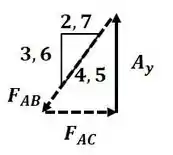
Aplicando semelhança de triângulos entre os triângulos de força e de comprimento, temos:
Pegando a primeira e terceira parcela, temos:
Pegando a segunda e terceira parcela, temos:
Agora vamos analisar o nó B:
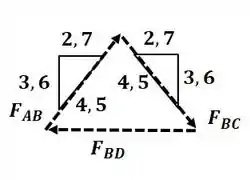
Aplicando semelhança de triângulos entre os triângulos de força e de comprimento, temos:
Pegando a primeira e terceira parcela, temos:
Pegando a segunda e terceira parcela, temos:
Agora vamos analisar o nó C:
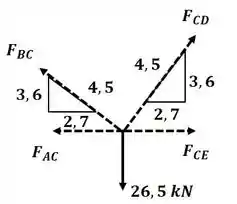
Aplicando o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Passo 3
Agora vamos analisar o nó D:
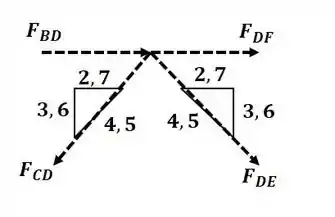
Aplicando o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Agora vamos analisar o nó F:
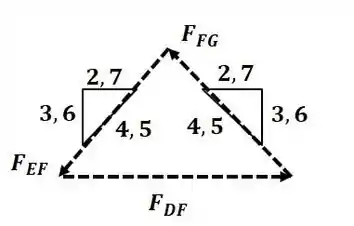
Aplicando semelhança de triângulos entre os triângulos de força e de comprimento, temos:
Pegando a primeira e terceira parcela, temos:
Pegando a segunda e terceira parcela, temos:
Agora vamos analisar o nó G:
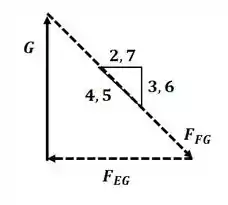
Aplicando semelhança de triângulos entre os triângulos de força e de comprimento, temos: