Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 13

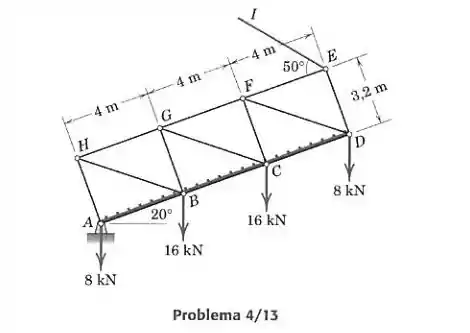
Uma ponte levadiça está sendo levantada por um cabo E I . As quatro cargas mostradas nos nós são devidas ao peso do pavimento. Determine as forças nos elementos E F , D E , D F , C D e F G .

Passo 1

Primeiro precisamos resolver as equações de equilíbrio externas ao conjunto, para achar a força de tração T . Vamos fazer a equação do momento em torno de A , pois não envolve as forças desconhecidas naquele ponto. Para simplificar, colocaremos o eixo x paralelo a A D . Então:

∑ M A = 0

⇒ - 16 cos ⁡ 20 ° ( 4 ) - 16 cos ⁡ 20 ° 8 - 8 cos ⁡ 20 ° 12 +   T cos ⁡ 50 ° 3,2 + T sen ⁡ 50 ° 12 = 0

⇒ - 288 cos ⁡ 20 ° + 3,2   T cos ⁡ 50 ° + 12 T sen ⁡ 50 ° = 0

⇒ 270,6 = 11,25 T ⇒ T = 24,05   k N

Passo 2

Agora vamos resolver as equações de equilíbrio em x e y   para cada nó. As forças positivas indicam tração e as negativas compressão, e sempre trataremos as forças desconhecidas como tração.

Nó E:

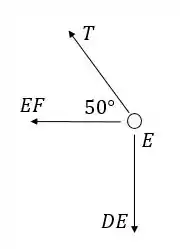
∑ F x = 0 ⇒ - E F - T cos ⁡ 50 ° = 0 ⇒ E F = - 24,05 cos ⁡ 50 ° ⇒ E F = - 15,46   k N   ( C )

∑ F y = 0 ⇒ - D E + T sen ⁡ 50 ° = 0 ⇒ D E = 24,05 sen ⁡ 50 ° ⇒ D E = 18,42   k N   ( T )

Passo 3

Nó D:

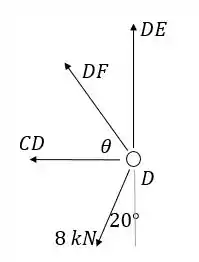
Precisamos obter o valor do ângulo θ = C D ^ F . Temos:

tg ⁡ θ = 3,2 4 = 0,8 ⇒ θ = arctg ⁡ ( 0,8 ) = 38,7 °

Agora vamos às equações em x e y (lembrando que o eixo x é paralelo a A D )

∑ F y = 0 ⇒ D E + D F sen ⁡ 38,7 ° - 8 cos ⁡ 20 ° = 0

Substituindo os valores:

18,42 + 0,6252   D F - 7,518 = 0 ⇒ 0,6252   D F = - 10,9

⇒ D F = - 17,46   k N   ( C )

∑ F x = 0 ⇒ - D F cos ⁡ 38,7 ° - C D - 8 sen ⁡ 20 ° = 0

⇒ 13,63 - C D - 2,736 = 0 ⇒ C D = 10,89   k N   ( T )

Passo 4

Nó F:

Como só estamos interessados em F G , fazemos só a equação para x :

∑ F x = 0 ⇒ - F G + E F + D F cos ⁡ 38,7 ° = 0

Substituindo o valor de E F e D F já encontrados:

- F G - 15,46 - 13,63 = 0

⇒ F G = - 29,09   k N   ( C )

Resposta

E F = 15,46   k N   ( C )

D E = 18,42   k N   ( T )

D F = 17,46   k N   ( C )

C D = 10,89   k N   ( T )

F G = 29,09   k N   ( C )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A treliça usada para sustentar um balcão está sujeita às cargas mostradas. Considere cada nó como um pino e determine a força em cada membro. Indique se os membros estão sob tração ou compressão. Faça
Considere que cada membro da treliça é feita de aço tendo uma massa por comprimento de 4k g / m . Faça P = 0 , determine a força em cada membro e indique se os membros estão sob tração ou compressão.
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão. Considere cada nó como um pino. Faça P = 4k N .
Determine a força em cada membro da treliça e diga se os membros estão sob tração ou compressão. Faça P 1 = 2k N , P 2 = 1,5k N .
Determine a força em cada membro da treliça e diga se os membros estão sob tração ou compressão. Faça P 1 = P 2 = 4k N .