Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 94

Suponto que a pressão entre as superfícies de contato seja uniforme, mostre que a intensidade M do binário necessário para se vencer a resistência de atrito para o mancal cônico mostrado é:

M = 2 3 ⋅ μ k P sin ⁡ θ ⋅ R 2 3 - R 1 3 R 2 2 - R 1 2

Passo 1

Bom galera, começamos já sabendo que:

Δ N Δ A = k r

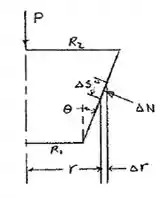
Então:

Δ N = k Δ A

→ Δ A = r Δ s Δ ϕ

→ Δ s = Δ r sin ⁡ θ

Passo 2

Show de bola, a força normal P é dada por:

P = lim Δ A → 0 ⁡ ∑ F y

→ P = ∫ 0 2 π ∫ R 1 R 2 k r d r d ϕ

→ P = 2 π k ∫ R 1 R 2 r d r

Logo podemos ter:

k = P π ( R 2 2 - R 1 2 )

Passo 3

Então, a força de fricção é:

Δ F = μ Δ N = μ k Δ A

E assim o momento fica:

Δ M = r Δ F = r μ k r Δ r sin ⁡ θ

O total fica:

M = lim ΔA → 0 ⁡ ∑ Δ M

→ M = ∫ 0 2 π ∫ R 1 R 2 μ k sin ⁡ θ r 2 d r d ϕ

→ M = 2 π μ k sin ⁡ θ ∫ R 1 R 2 r 2 d r

→ M = 2 π μ P 3 sin ⁡ θ π R 2 2 - R 3 2 ( R 2 3 - R 3 3 )

Assim, chegamos á:

→ M = 2 π μ P ( R 2 3 - R 3 3 ) 3 sin ⁡ θ π ( R 2 2 - R 3 2 )

Resposta

M = 2 π μ P ( R 2 3 - R 3 3 ) 3 sin ⁡ θ π ( R 2 2 - R 3 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Assumindo que a variação de pressão no fundo do mancal axial seja definida como p = p o ( R 2 r ) , determine o torque M necessário para superar o atrito se o eixo está sujeito a uma força axial P . O
A polia é suportada por um pino de 25m m de diâmetro. Se a polia se ajusta livremente no pino, determine a menor força P necessária para levantar o balde. O balde tem uma massa de 20k g e o coeficient
Os cilindros são suspensos a partir da extremidade da barra que se ajusta livremente em um pino com diâmetro de 40m m . Se A tem uma massa de 10k g , determine a massa exigida de B que seja suficiente
Resolve o problema anterior se a força P for aplicada horizontalmente para a direita.
A polia de 5k g tem um diâmetro de 240m m e o eixo tem um diâmetro de 40m m . Se o coeficiente de atrito cinético entre o eixo e a polia μ k = 0,15 , determine a força vertical P na corda necessária p