Um suporte, em forma de paralelogramo, proposto para uma luminária ajustável é mostrado. Se o comprimento não esticado da mola é , determine a rigidez da mola necessária para haver equilíbrio em dado ângulo com a vertical. A massa da luminária e da peça triangular é . Verifique a estabilidade dentro da faixa de trabalho de até .
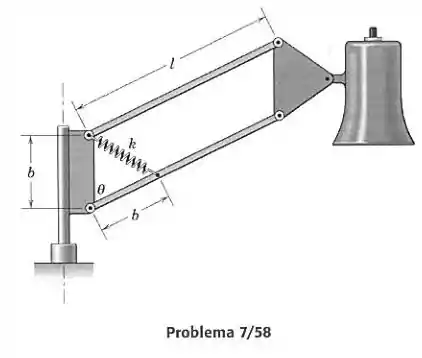
Passo 1
Se representarmos a energia potencial do sistema em função do ângulo , como não há outras forças ativas (que realizam trabalho) além do peso e da força elástica da mola, a condição para o equilíbrio é dada por:
E a condição adicional para o equilíbrio estável é:
A energia potencial do sistema varia com a altura do centro de massa do pêndulo e do alongamento da mola. Vamos então encontrar a relação de com , e depois aplicar as derivadas.
Passo 2
Primeiro vamos calcular a energia potencial devida à mola em função de . Vamos definir que quando a mola não está alongada nem comprimida. Então calculamos o comprimento da mola:
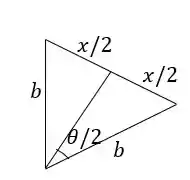
Se o comprimento normal da mola é , então a deformação é dada por:
Tendo valor positivo quando a mola está alongada e negativo quando está comprimida. O potencial elástico da mola é então:
Passo 3
Agora calculamos a energia potencial gravitacional da luminária e da peça triangular. Vamos definir para , quando os braços que seguram as peças são horizontais. A variação da altura do centro de massa da luminária e da peça em relação a essa posição pode ser então dada por:
Então a energia potencial gravitacional é:
Passo 4
A energia potencial total do sistema é então dada por:
Derivamos a expressão em relação a :
Como :
A condição de equilíbrio diz que a derivada deve ser zero, então achamos :
Para simplidicar, dividimos em cima e em baixo por :
Passo 5
A condição de estabilidade é que a segunda derivada seja positiva. Derivando novamente :
A partir da expressão de , podemos obter um valor para :
Substituindo então na expressão da segunda derivada:
O valor de para é:
Então o valor vai aumentando com a diminuição de até , onde o valor de é:
A segunda derivada então é infinita para , e vai diminuindo até , onde o seu valor é:
Agora substituindo o valor de para :
Então a segunda derivada é muito grande para e depois se aproxima de quando , se mantendo positiva. Logo, o teremos equilíbrio estável.