Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas de Revisão - Ex. 252

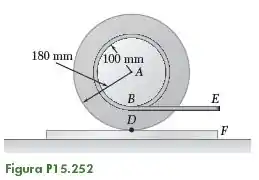
Um tambor de 100 mm de raio está preso rigidamente a um cilindro de 180 mm de raio. Uma corda é enrolada ao redor do tambor e sua extremidade E é puxada para a direita com velocidade constante de 400 mm/s, fazendo com que o cilindro role sem deslizar na placa F. Sabendo que a placa F é fixa, determine (a) a velocidade do centro do cilindro, (b) a aceleração do ponto D do cilindro.

Passo 1

Este exercício nos pede a velocidade e aceleração de C . Vamos organizar nossos dados do enunciado. Temos que:

ω 1 = 9   r a d / s

ω 2 = 12   r a d / s

α 1 = - 45   r a d / s 2

α 2 = - 60   r a d / s 2

O vetor posição C com relação a A é dado por:

r C / A = 0 , 135   m j + 0 , 09   m k

Temos também que:

Ω = ω 1 k = 9   r a d / s k

Ω ˙ = α 1 k = - 45   r a d / s 2 k

Sabemos que a velocidade escalar do ponto C é dada por:

v C = v C ' + v C / F

Onde:

v C ' = Ω × r C / A

Vamos aos cálculos.

Passo 2

Temos que:

v C ' = Ω × r C / A

v C ' = 9   r a d / s k × 0,135   m j + 0,09   m k

v C ' = - 1,215   m / s i

A velocidade relativa entre C e A E pode ser representada na forma vetorial:

v C / F = ω 2 × r C / A

v C / F = 12   r a d / s i × 0,135   m j + 0,09   m k

v C / F = 1,62   m / s k - 1,08   m / s j

Logo, a velocidade escalar do ponto C será:

v C = v C ' + v C / F

v C = - 1,215   m / s i + 1,62   m / s k - 1 , 08   m / s j

Passo 3

Para a aceleração do ponto C , temos que:

a C = a C ' + a C / F + 2 Ω × v C / F

Temos que:

a C ' = Ω ˙ × r C / A + Ω × v C '

Portanto:

a C ' = - 45   r a d / s k × 0,135   m j + 0,09   m k × 9   r a d / s k × - 1,215   m i

a C ' = 6,075   m / s 2 i + - 10,935   m / s 2 j

Temos também que:

a C / F = ω ˙ 2 × r C / A + ω 2 × v C / F

Logo:

a C / F = - 60   r a d / s i × [ 0,135   m j + 0,09   m k ] + 12   r a d / s i × [ 1,62   m / s k - 1,08   m / s j ]

a C / F = - 14,04   m / s 2 j + - 21,06   m / s 2 k

Passo 4

Portanto:

a C = a C ' + a C / F + 2 Ω × v C / F

a C = 6,075   m / s 2 i + - 10,935   m / s 2 j + - 14,04   m / s 2 j + - 21,06   m / s 2 k + 2 9   r a d / s k × [ 1,62   m / s k - 1 , 08   m / s k ]

Resolvendo, temos que

a C = 25,5   m / s 2 i - 25   m / s 2 j - 21,1   m / s 2 k

Resposta

v C = - 1,215   m / s i + 1,62   m / s k - 1,08   m / s j

a C = 25,5   m / s 2 i - 25   m / s 2 j - 21,1   m / s 2 k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa retangular mostrada na figura gira à taxa constante ω 2 = 12r a d / s em relação ao braço A E , que, por sua vez, gira à taxa constante ω 1 = 9r a d / s em torno do eixo Z . Para a posição mos
Resolva o Problema 15.228 admitindo que, no instante mostrado na figura, a velocidade angular ω 2 da placa em relação ao braço A E é de 12r a d / s e decresce à taxa de 60r a d / s 2 , enquanto a velo
A placa retangular mostrada na figura gira à taxa constante ω 2 = 12r a d / s em relação ao braço A E , que, por sua vez, gira à taxa constante ω 1 = 9r a d / s em torno do eixo Z . Para a posição mos
Usando o método da Seção 15.14 , resolva o Problema 15.191 .
Usando o método da Seção 15.14 , resolva o Problema 15.19 5 .