Uma viga extrudada tem seção transversal como mostrado e uma espessura de parede constante e igual a . Para uma força cortante vertical de , determinar:
- A tensão de cisalhamento no ponto A
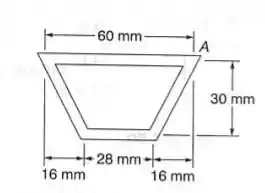
Passo 1
Nosso objetivo é determinar a tensão cisalhante no ponto A, para isso temos que calcular a tensão no meio de cada uma das seções:
Em que:
Para esse ponto, já sabemos algumas coisas que vão ser importantes para a gente, que são:
Agora precisamos determinar o momento estático e o momento de inércia, para isso temos um passo a passo, uma que vamos determinar a LN e um que vamos determinar o momento de inércia e estático, assim, vamos ver isso nos passos seguintes.
Passo 2
Para determinarmos a LN, precisamos determinar a Área e a distância do centroide de cada um dos trechos até a base da nossa peça, assim, podemos dividir a nossa seção em seções mais simples, e assim teremos que:
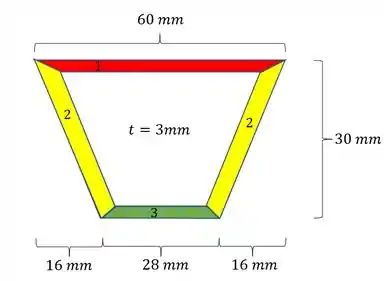
Assim temos que as áreas 1 e 3 podem ser determinadas diretas, desse modo teremos que:
E a área 2? Essa basta fazermos um Pitágoras para achar o comprimento dela na diagonal e multiplicarmos pela espessura, assim temos que:
Basta agora determinarmos a distancia do centroide de cada seção até a base da estrutura, onde teremos que:
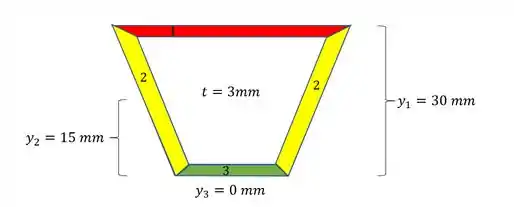
Como a espessura é muito pequena, desprezamos ela no cálculo, por esse motivo que é iguala zero.
Tendo isso tudo podemos calcular a nossa LN pela equação:
Passo 3
Para determinarmos o momento de inércia, precisamos determinar a distância do centroide de cada elemento até a LN, o momento de inércia de cada seção, e a área podemos ficar tranquilos porque já temos, então, vamos determinar primeiro a distancia dos centroides até a a LN.
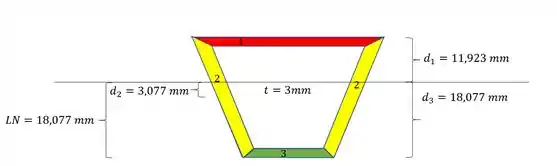
Para os momentos de inércia, o 2 vai ser o que vamos ter que ter uma atenção maior, mas o 1 e 3 podemos ver o seguinte, sabemos que seu calculo vai ser dado por:
Como as espessuras são muito pequenas, podemos considerar elas aproximadamente zero, assim definimos que:
Para vamos fazer algo diferente do que fizemos na área, lá nos mudamos a altura para o comprimento L e mantivemos a espessura, agora, para facilitar o cálculo, eu vou manter a altura, e modificar a espessura, assim teremos que:
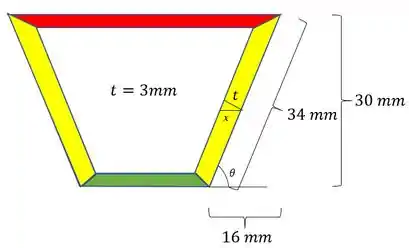
E sabemos que podemos fazer a seguinte relação:
Assim o momento de inércia em 2 pode ser visto como:
Assim a nossa equação para o momento de inércia vai ser dada por:
Substituindo, teremos que:
Agora só precisamos do nosso momento estático.
Passo 4
Para o momento estático precisamos determinar a área acima do ponto que queremos calcular a tensão cisalhante, e a distância dessa área até a nossa LN, mas, no caos de espessuras muito finas, usamos a própria área da espessura e a distancia dela até a nossa LN, ou seja, como o ponto A está em cima, basta usarmos os seguintes dados:
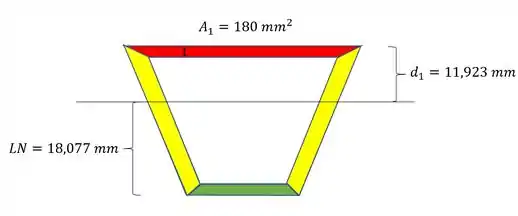
- Tensão no ponto A