Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 68

A viga AB suporta duas cargas concentradas P e Q. A tensão normal devido a flexão na borda inferior da seção transversal da viga é de + 55MPa em D e 37,5 MPa em F. Pede-se a) desenhar os diagramas de forca cortante e de momento fletor para a viga b) determinar a máxima tensão normal que ocorre na viga devido a flexão.

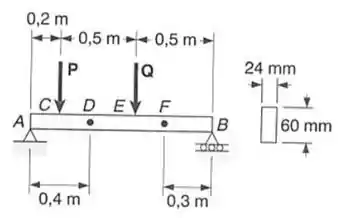
Passo 1

Fala aíi gurizada tudo belezinha, espero que simm!!!! Para entendermos melhor a questão vamos fazer um esquema de diagrama de corpo livre? Vejam abaixo!!!

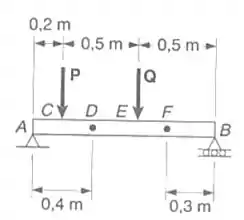
E agora vamos achar o momento em a...

+ ↶ ∑ M a = F × d = 0

+ ↶ ∑ M D = - P × 0 , 2 - 0,7 × Q + 1,2   V B

- 0,2 P - 0,7 Q = - 2,16

Agora iremos calcular o momento em F, vem comigo ;), antes vamos desenhar o DCL

Gurizada agora que encontramos os momentos vamos fazer o somatório das forças, venha!!!

+ ↑ ∑ F v = 0

∑ F v = V A - P - Q + V B = 0

Agora teremos que realizar o momento em D.

+ ↶ ∑ M D = 0

M D =   V A × 0 , 4 - P × 0,2

M D = 0,4 V A - 0,2 P

Calculando momento em F temos:

+ ↶ ∑ M f = 0

M f = 0,3 V B

Passo 2

Gurizada observem que nós ficamos com 3 equações com 3 incognitas, notem que caira em um sistema 3x3 , mas teremos que encontrar os momentos em D e F para igualar nas equações acima, vejam...

Lembrando que a equação da tensão é dada abaixo, lembrando que a inércia é dada no anexo do livro.

σ = m d C i

55 = m d × 30 4 32000

m d = 0,792   × 10 6   N m m

Para o momento em f calculamos da mesma maneira...

37 , 5 = m f × 30 432000

m f = 0,54 × 10 6   N m m

Passo 3

Agora sim podemos resolver o sistema veja:

V A - P - Q = - 1,8

0 V A - 0,2 P - 0,7 Q = - 2,16

0,4 V A - 0,2 P + 0 Q = 0,792

Resolvendo o sistema temos os seguintes valores:

P = 3,24   K N

V A = 3,6   K N

Q = 2,16   K N

Agora podemos desenhar o cortante :D

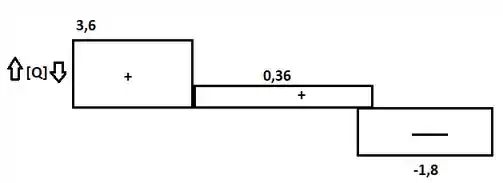
E para o momento máximo temos:

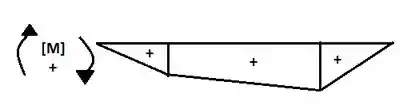
Passo 4

Agora sim gurizada podemos encontrar a tensão máxima

Lembrando que a equação da tensão é dada abaixo, lembrando que a inércia é dada no anexo do livro.

σ = m C i

σ = 0,9   × 10 6 × 30 432000 = 62,5   M P a

Resposta

σ = 62,5     M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas placas de cobertura, cada uma com 18m m de espessura e 220m m de largura, são soldadas a uma viga de perfil laminado W 410 × 85 , como mostrado. Sabendo-se que P = 185k N , determinar a máxima te
Resolver o Prob. 7.146, considerando que a porção C D das placas de cobertura tem 2,5m de comprimento.
Duas placas de cobertura, cada uma com 12,7m m de espessura e 250m m de largura, são soldadas a uma viga de perfil laminado W 360 × 79 . Sabendo-se que σ a d m = 150M P a e τ a d m = 90M P a , determi
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares,escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o máximo m
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares,escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o máximo m