Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 81

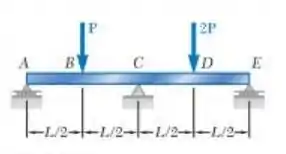
Para a viga uniforme mostrada, determine a reação em cada um dos três apoios.

Passo 1

Fala aí, galera. Tudo beleza? Vamos fazer mais uma questão pra tirar aquele notão na prova.

Para determinarmos as reações nos três apoios, temos que dividir esta viga em casos de superposição. Neste caso, serão três tipos de carregamento.

Primeiro, temos que o carregamento I corresponde ao caso 4 do apêndice D . Portanto, sua deflexão no ponto B vai ser:

y C I = - F C ( 2 L ) 3 48 E I

y C I = F C L 3 6 E I

O carregamento I I corresponde ao caso 5 . Para a deflexão no ponto C , temos:

y C I I = P b 6 E I 2 L x 3 - 2 L 2 - b 2 x y C I I = - 11 P L 3 48 E I

Já o terceiro carregamento é do tipo 5 do nosso livro. Desta vez, para o segmento C B . Logo:

y C I I I = 2 y C I I

y C I I I = - 11 P L 3 24 E I

Agora que conseguimos todos os carregamentos de superposição, vamos determinar as reações.

Passo 2

Então, agora que encontramos a deflexão e a inclinação para cada caso de superposição, vamos utilizar a deflexão no ponto C , que é 0 e é dada pela soma das deflexões dos três casos de superposição. Portanto:

y C = y C I + y C I I + y C I I I = 0 F C L 3 6 E I - 11 P L 3 48 E I - 11 P L 3 24 E I = 0 F C = 33 16 P

Passo 3

Agora que determinamos a reação em A , vamos utilizar as equações de equilíbrio para determinarmos as reações restantes. Temos:

∑ M E = 0 F A 2 L + P 3 L 2 - 33 16 P L + 2 P L 2 = 0 F A = 7 32 P

E também, para a reação em E , temos:

∑ F y = 0 F E - 2 P + 33 16 P - P + 7 32 P = 0 F E = 23 32 P

Mais uma questão resolvida, galera! Bora fazer mais?.

Resposta

F C = 33 16 P

F A = 7 32 P

F E = 23 32 P

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento do P r o b . 9.49 , determinar a maior deflexão, para cima, no vão AB.Segundo a localização do ponto que ocorre o máximo para a Viga e carregamento do P r o b . 9 . 4 9 .
Para a viga e o carregamento do P r o b . 9.49 , determinar a maior deflexão, para cima, no vão AB.Primeiro determinar a inclinação do ponto A para a Viga e carregamento do P r o b . 9 . 4 9 .
Para a viga e o carregamento do P r o b . 9.49 , determinar a maior deflexão, para cima, no vão AB.A intensidade do máximo para a Viga e carregamento do P r o b . 9 . 4 9 .
Para a viga e o carregamento do P r o b . 9.5 3 , determinar a maior deflexão, para cima, no vão DE.Primeiro determinar a inclinação do ponto D para a Viga e carregamento do P r o b . 9.5 3 .
Para a viga e o carregamento do P r o b . 9 . 50 , determinar a maior deflexão, para cima, no vão EB.A intensidade do máximo para a Viga e carregamento do P r o b . 9 . 50 .