Solução de Pórticos Simples – até 2 barras por nó
Teoria
Agora que já sabemos como determinar se meu pórtico é Isostático, hipostático ou ainda hiperestático, vamos ver o que o professor pode tramar maldosamente pedir para nós em um pórtico.
O professor, em pórticos, pode pedir tudo que ele poderia pedir em treliças, ou seja, o professor pode pedir
- Reações de apoio
- Balanceamento de equações
- Valores nas extremidades das barras
- Valores nos encontros de barras
- Verificação das rótulas (quando existirem)
- Diagrama de cortante, fletor, normal.
Agora que já sabemos o que os professores podem nos pedir nas nossas provas, vamos fazer um exercício passo a passo, pra ficar tranquilo o entendimento.
Situação
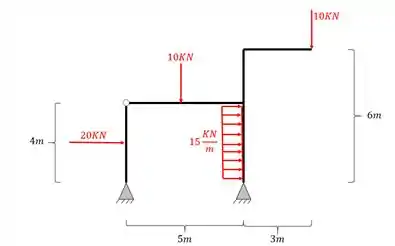
Imagine chegar na prova e se deparar com um pórtico desses, e a pergunta é bem simples, qual o diagrama de momentos fletores desse pórtico?
Vamos pegar todos os macetes no nosso passo a passo.
Primeiro passo: balanceamento de incógnitas
Como vimos na aula de conceito, o balanceamento de incógnitas é muito importante para sabermos como proceder, então para isso vamos ver se o nosso pórtico atende as nossas regras.
Primeiro temos os dois apoios, que nos darão 4 incógnitas
Como não tem tirante, o total de incógnita será 4 mesmo.
Agora o número de equações: pra isso já sabemos que temos as nossas 3 equações de equilíbrio
E sabemos que o número de equações ligada as rótulas estão ligas ao numero de barras que chegam nessa rótula, nos nosso caso, como chegam duas barras nas rótulas, teremos mais 1 equação
Logo, no balanceamento nós temos 4 equações e 4 incógnitas, e como temos pelo menos 1 vetor em cada direção, podemos dizer que o nosso problema é isostático.
Segundo passo: Reações de apoio
Agora que sabemos que o nosso problema é isostático, vamos achar as reações de apoio, para isso, usaremos a nossas 4 equações.
- Numerar cada nó
- Calcular os esforços de cada lado do nó quando somente existirem 2 barras nesse nó ( como na nossa situação só tem que descobrir o valor do momento, só iremos nos preocupar com esse esforço, mas se pedir todos os diagramas, será o mesmo processo feito para o momento fletor, só que para outros esforços.)
- Se no nó chegarem 3 barras ou mais, fazer o cálculo para cada uma das barras de cada vez
- Verificar as rótulas
- Desenhar os diagramas
Olhando o nosso pórtico teremos o seguinte: Substituindo os apoios
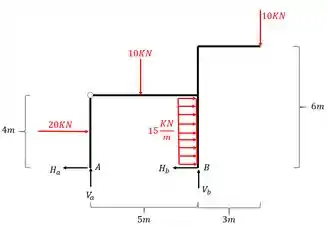
Precisamos fazer o somatório de momentos em A igual a zero (considerar todas as cargas concentras aplicadas no meio das suas barras), com isso teremos
Como já vimos em treliça, quando da negativo eu costumo inverter o sinal do vetor, e considerar ele, positivo, pra até facilitar os cálculos.
Essa é a equação que conseguimos pela rótula, como já sabemos, o somatório de momentos na rótula tem que ser igual a zero, tanto se fizermos o somatório pela esquerda ou pela direita. Se fizermos o somatório pela esquerda, só consideramos as cargas da esquerda. Se fizermos pela direita, só consideramos as cargas da direita, com isso teremos que
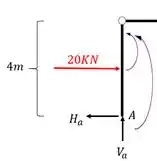
Perceba que ignoramos completamente tudo que tem do lado direito da barra, e vamos fazer o somatório de momentos, na rótula, apenas pelo lado esquerdo dela, com isso teremos
Perceba que não entra na conta pois não possui braço de alavanca com relação a rótula.
Como já determinamos o valo de todas as incógnitas, podemos ver como os vetores agem no nosso pórtico
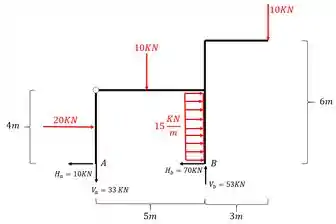
Agora que já temos as reações de apoio, vem a parte mais complicada: o desenho do diagrama. Pra isso teremos que tomar muito cuidado, por isso tem o seguinte macete pra resolver.
Terceiro passo: Valores na extremidade de cada nó
Vamos primeiro numerar os nós, e calcular todos os esforços que ocorrem nos nós que possuem apenas duas barras
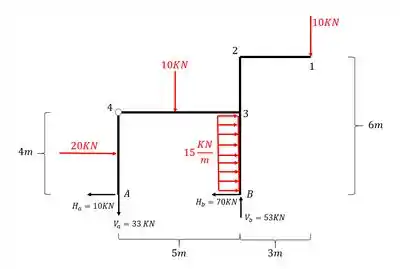
Veja que os dois primeiros nós representamos a extremidade da barra (nó 1) e um nó com duas barras (nó 2).
Como o nosso interesse é somente momentos fletores, sabemos que no nó 1 teremos braço de alavanca igual a zero, e nesse caso, o nosso momento será zero, o que eu gosto de fazer é ir marando momentos com o numero do nó que eu já calculei, e quando eu for pro próximo nó eu elimino tudo que tiver depois dele, e levo até lá tudo que eu tirei, como assim ?
Vamos ver no nosso desenho:
Primeiro eu calculei que o momento em 1 é zero
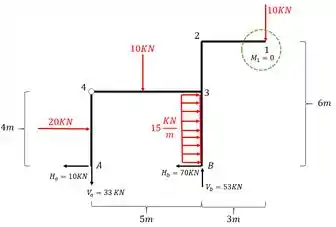
Agora eu tenho que ir pro nó 2 ( é importante marcar os nós em sequência pro método funcionar direitinho), para eu ir pro nó 2, eu arranco tudo que tem antes dele, e qualquer carga que for retirada eu levo até ele
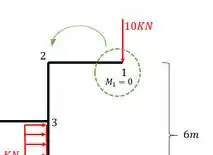
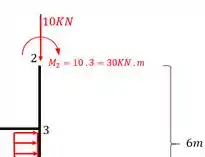
Perceba que como não me importa esforços normais e cisalhante, eu não precisaria levar a carga de 10, apenas o momento, que é o que importa, mas eu levei a carga de 10 para vc ver como vai proceder para outros esforços, sendo nesse caso a carga de 10 um cisalhante para a barra 1-2 e um normal para a barra 2-3, mas como esse não é o enfoque, vamos deixar apenas o que nos importa.
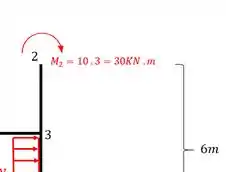
Um cuidado que vale lembrar é que sempre que houver mudança de barrar você tem que ver se todo o esforço vai ser transferido para outra barra. Como nesse caso não tem nenhum memento aplicado no nó 2, sabemos que será tudo transferido. Porém se a situação fosse essa
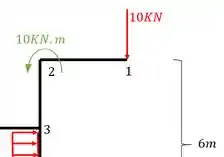
Quando levássemos o momento para o nó 2 teríamos o seguinte
Antes do nó 2 mas muito próximo dele
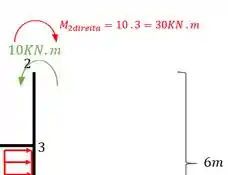
Veja que temos nesse caso um momento a direita do nó 2, que é exatamente o momento que calculamos na situação anterior e está na barra 1-2. Já do lado esquerdo teríamos
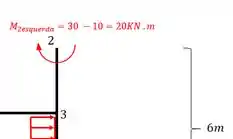
Agora tiramos o momento concentrado no nó 2 e colocamos ele como contribuição do lado esquerdo do nó, ou seja, na barra 2-3. Ou seja, no mesmo nó temos um momento a direita e outro a esquerda, mas isso só ocorre no caso de concentração de esforços em um ponto, nesse caso a concentração seria de um momento no nó.
Até aqui aprendemos a resolver metade do pórtico, mas ainda precisamos aprender a resolver nós com 3 barras, porém isso destinamos a parte 2 dessa aula, vamos lá para finalizar esse módulo de aula, bora lá???
Primeiro passo: balanceamento de incógnitas
Segundo passo: Reações de apoio
Terceiro passo: Valores na extremidade de cada nó
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Calcule as reações de apoio do pórtico simples mostrado.
Passo 1
Para resolvermos qualquer exercício de pórticos simples, precisamos seguir uma sequência de passos que irá nos ajudar na solução desse tipo de problema, e a sequência é a seguinte.
- A primeira coisa que devemos fazer é o cálculo das reações de apoio, pois assim conseguiremos calcular qualquer nó sem que haja nenhum problema.
- a segunda coisa é seguir a seguinte sequência de nós a serem resolvidos:
Nós com 2 barras
Nós com 3 barras
Nós com 4 barras
...
- A terceira coisa que devemos fazer é calcular o valor dos momentos fletores, cortantes e normais em todos as barras que chegarem ou saírem de algum nó
- O quarto e último passo consiste em desenhar os diagramas do pórtico quando esse for pedido.
Agora que já sabemos qual sequência de passos devemos seguir, vamos aplicar esse conhecimento ao nosso problema.
Passo 2
Como vimos, a primeira coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E assim resolvemos o nosso problema, vamos para o próximo.
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule as reações de apoio do pórtico simples mostrado.
Passo 1
Para resolvermos qualquer exercício de pórticos simples, precisamos seguir uma sequência de passos que irá nos ajudar na solução desse tipo de problema, e a sequência é a seguinte.
- A primeira coisa que devemos fazer é o cálculo das reações de apoio, pois assim conseguiremos calcular qualquer nó sem que haja nenhum problema.
- a segunda coisa é seguir a seguinte sequência de nós a serem resolvidos:
Nós com 2 barras
Nós com 3 barras
Nós com 4 barras
...
- A terceira coisa que devemos fazer é calcular o valor dos momentos fletores, cortantes e normais em todos as barras que chegarem ou saírem de algum nó
- O quarto e último passo consiste em desenhar os diagramas do pórtico quando esse for pedido.
Agora que já sabemos qual sequência de passos devemos seguir, vamos aplicar esse conhecimento ao nosso problema.
Passo 2
Como vimos, a primeira coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
Invertendo o vetor teremos que
E assim resolvemos o nosso problema, vamos para o próximo.
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule as reações de apoio do pórtico simples mostrado.
Passo 1
Para resolvermos qualquer exercício de pórticos simples, precisamos seguir uma sequência de passos que irá nos ajudar na solução desse tipo de problema, e a sequência é a seguinte.
- A primeira coisa que devemos fazer é o cálculo das reações de apoio, pois assim conseguiremos calcular qualquer nó sem que haja nenhum problema.
- a segunda coisa é seguir a seguinte sequência de nós a serem resolvidos:
Nós com 2 barras
Nós com 3 barras
Nós com 4 barras
...
- A terceira coisa que devemos fazer é calcular o valor dos momentos fletores, cortantes e normais em todos as barras que chegarem ou saírem de algum nó
- O quarto e último passo consiste em desenhar os diagramas do pórtico quando esse for pedido.
Agora que já sabemos qual sequência de passos devemos seguir, vamos aplicar esse conhecimento ao nosso problema.
Passo 2
Como vimos, a primeira coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E assim resolvemos o nosso problema, vamos para o próximo.
Resposta
Exercício Resolvido #4
Elaboração Própria
Calcule o valor do momento fletor, cortante e normal nos nós C e B do pórtico abaixo.
Passo 1
Para resolvermos qualquer exercício de pórticos simples, precisamos seguir uma sequência de passos que irá nos ajudar na solução desse tipo de problema, e a sequência é a seguinte.
- A primeira coisa que devemos fazer é o cálculo das reações de apoio, pois assim conseguiremos calcular qualquer nó sem que haja nenhum problema.
- a segunda coisa é seguir a seguinte sequência de nós a serem resolvidos:
Nós com 2 barras
Nós com 3 barras
Nós com 4 barras
...
- A terceira coisa que devemos fazer é calcular o valor dos momentos fletores, cortantes e normais em todos as barras que chegarem ou saírem de algum nó
- O quarto e último passo consiste em desenhar os diagramas do pórtico quando esse for pedido.
Agora que já sabemos qual sequência de passos devemos seguir, vamos aplicar esse conhecimento ao nosso problema.
Passo 2
Como vimos, a primeira coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em E vindo pela esquerda, teremos que
Logo
Relacionando os sistemas teremos que
logo
Conhecendo conhecemos também , substituindo, teremos
Sabemos que quando encontramos negativo significa que basta invertemos o vetor para calcularmos o valor positivo.
Por fim, podemos determinar o valor de , substituindo teremos
E dessa forma terminamos o primeiro passo que consiste em determinar o valor das reações de apoio. Vamos então ao próximo passo.
Passo 2
agora vemos que na sequência do nosso passo a passo devemos começar resolvendo os nós que possuem apenas 2 barras, e que no nosso problema são exatamente os nós que foram pedidos para a solução no enunciado. Sabemos que a primeira coisa que devemos fazer é cortar o pórtico no nó que iremos calcular e levarmos até esse nó todos os esforços que foram descartados com o corte do pórtico, começando pelo nó B teremos
Perceba que o corte que faremos irá dispensar o carregamento de 300 KN, logo, devemos levar para o nó tudo aquilo que seria perdido com a carga de 300KN, com isso teremos
Ou seja, podemos dizer que no nó B temos uma carga de 300 KN e um momento fletor de 900 KN.m agindo no nosso nó B, e como não temos nenhum carregamento no nó B, o seu equilíbrio será
Vemos que na barra AB a carga de 300 é cortante, mas na barra BC ela é normal, e ainda sim o nosso nó B está equilibrado. E quanto ao momento fletor o momento vai crescendo até 900 na barra AB e na barra BC será constante o valor de 900 por todo o comprimento da barra.
Feito o equilíbrio do nó B vamos ao nó C.
Passo 3
Sabemos que a primeira coisa que devemos fazer é cortar o pórtico no nó que iremos calcular e levarmos até esse nó todos os esforços que foram descartados com o corte do pórtico, fazendo isso para o nó C teremos
Perceba que o corte que faremos irá dispensar o carregamento de 300 KN, logo, devemos levar para o nó C tudo aquilo que seria perdido com a carga de 300KN, com isso teremos
Ou seja, podemos dizer que no nó C temos uma carga de 300 KN e um momento fletor de 900 KN.m agindo no nosso nó C, porém temos carregamentos no nó C, e por isso seu equilíbrio será
Vemos que na barra BC a carga de 300 é normal de tração, mas na barra CD ela é, junto cm a carga de 100 KN cortante, e ainda sim o nosso nó C está equilibrado. E quanto ao momento fletor o momento é constante a 900 na barra BC e na barra CD irá crescendo a partir de 900 no nó C e irá aumentar até o nó D. E quanto ao esforço normal, vemos que na barra CD haverá um esforço normal devido ao carregamento de 150 KN. Dessa forma fizemos também o equilíbrio do nó C.
Resposta
Nó B (barras AB e BC)
Nó C (barras BC e CD)
Exercício Resolvido #5
Elaboração Própria
Calcule o equilíbrio dos nós E e B do pórtico abaixo.
Passo 1
Para resolvermos qualquer exercício de pórticos simples, precisamos seguir uma sequência de passos que irá nos ajudar na solução desse tipo de problema, e a sequência é a seguinte.
- A primeira coisa que devemos fazer é o cálculo das reações de apoio, pois assim conseguiremos calcular qualquer nó sem que haja nenhum problema.
- a segunda coisa é seguir a seguinte sequência de nós a serem resolvidos:
Nós com 2 barras
Nós com 3 barras
Nós com 4 barras
...
- A terceira coisa que devemos fazer é calcular o valor dos momentos fletores, cortantes e normais em todos as barras que chegarem ou saírem de algum nó
- O quarto e último passo consiste em desenhar os diagramas do pórtico quando esse for pedido.
Agora que já sabemos qual sequência de passos devemos seguir, vamos aplicar esse conhecimento ao nosso problema.
Passo 2
Como vimos, a primeira coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em D vindo pela direita, teremos que
Logo
Relacionando os sistemas teremos que
logo
Isolando teremos
Isolando do outro sistema teremos que
Tendo os valores de e basta substituirmos no terceiro sistema, que é dado por
Substituindo as próximas reações de apoios teremos que
Agora que já temos as reações de apoio, vamos ao equilíbrio dos nós.
Passo 2
Agora vemos que na sequência do nosso passo a passo devemos começar resolvendo os nós que possuem apenas 2 barras, e que no nosso problema são exatamente os nós que foram pedidos para a solução no enunciado. Sabemos que a primeira coisa que devemos fazer é cortar o pórtico no nó que iremos calcular e levarmos até esse nó todos os esforços que foram descartados com o corte do pórtico, começando pelo nó B teremos
Perceba que o corte que faremos irá dispensar as reações do apoio A, e o carregamento de 40KN, logo, devemos levar para o nó tudo aquilo que seria perdido tanto com relação aos apoios, quanto com relação aos carregamentos, sendo assim o nosso nó B ficaria
Juntando os carregamentos com mesmo direcionamento, teremos que
Equilibrando o nó B teremos que
Vemos que na barra AB a carga de 112,59 é cortante, mas na barra BC ela é normal, e ainda sim o nosso nó B está equilibrado. E quanto ao momento fletor o momento vai crescendo até 719,24 na barra AB e na barra BC será crescente a partir de 719,24 por todo o comprimento da barra.
Feito o equilíbrio do nó B vamos ao nó E.
Passo 3
Sabemos que a primeira coisa que devemos fazer é cortar o pórtico no nó que iremos calcular e levarmos até esse nó todos os esforços que foram descartados com o corte do pórtico, fazendo isso para o nó E teremos
Perceba que o corte que faremos irá dispensar as reações de apoio em F, logo, devemos levar para o nó E tudo aquilo que seria perdido quando retirássemos essa barra, com isso teremos
Equilibrando o nó E teremos que
Vemos que na barra EF a carga de 6,17 é normal de compressão, mas na barra ED ela é cortante, e ainda sim o nosso nó E está equilibrado. E quanto ao momento fletor o momento cresce até 18,52 na barra EF e na barra ED ele começa com 18,52 e decresce até zero no nó. E quanto ao esforço normal, vemos que na barra ED haverá um esforço normal devido ao carregamento de 120 KN mais a carga de 7,41 que é cortante na barra EF. Dessa forma fizemos também o equilíbrio do nó E.
Resposta
Nó B (barras AB e BC)
Nó E (barras EF e ED)
