Teoria
Introdução
No ultimo capitulo estudamos sobre treliças, e pensamos diversas formas de saber o que é uma treliça e como resolve-las. Nesse capitulo também iremos definir um pórtico, para isso temos eu ter em mente o seguinte
- O pórtico, diferente das treliças, não possui rótulas em todos os seus nós
- Nó pórtico teremos ação de esforços normais, cortante e momento fletor
- Os pórticos se classificam em simples, compostos, simples com tirante, compostos com tirante.
- As cargas nos pórticos não precisam necessariamente estar aplicada nos nós, se houver algum nó nesse pórtico.
Mas qual cara meus pórticos podem ter?

Pórticos simples
Podemos definir um pórtico simples, como um pórtico que não precisamos quebrar alguma rótula e fazer uma análise para cada pedaço do pórtico. Pelo contrário, conseguimos fazer todas a analises necessárias do nosso pórtico apenas usando as formulas de equilíbrios de força que temos. Vamos ver alguns exemplos aqui em baixo.
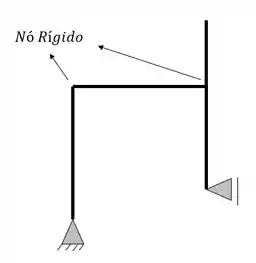
Nós rígidos são nós que armazenam momento fletor, diferentemente das rótulas que sabemos ter momento fletor igual a zero, por isso as nossas treliças possuíam apenas nós rotulados, os pórticos não possuem obrigatoriedade de possuir nós rotulados.
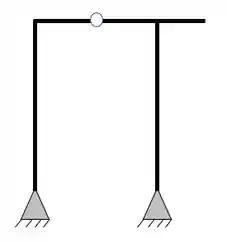
Nesse pórtico, como veremos mais adiante a presença da rótula possibilita determinarmos mais uma equação que nos ajudará na solução dessa questão.
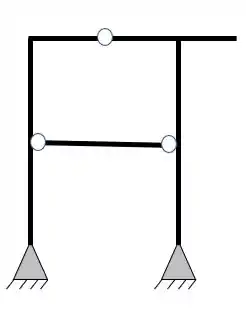
Já esse pórtico apresenta algo novo para nós. Perceba que a barra do meio apresenta duas rótulas, como uma treliça. Ou seja, assim como uma treliça ela não terá esforços cortantes e fletores, apenas esforço normal. Nesse caso podemos chamar essa barra de tirante ou de cabo, mas que veremos como resolver em outros tópicos.
Mas como podemos saber que os nossos pórticos acima são simples?
Equilíbrio de equações e incógnitas
Para termos a certeza de que se trata de um pórtico simples temos que fazer o balanço de equações e incógnitas. Começado pelas equações, temos que saber que dois grupos principais nos darão as equações.
O primeiro grupo são as nossas velhas conhecidas equações de equilíbrio
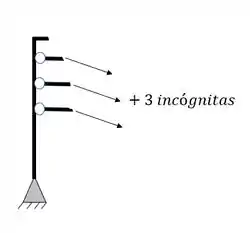
O segundo grupo vem das Rótulas, e para sabermos quantas equações as rótulas nos dão, basta subtrair 1 do número de barras que chegam ou saem de uma mesma rótula, por exemplo
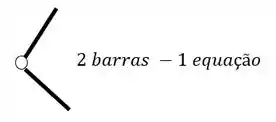
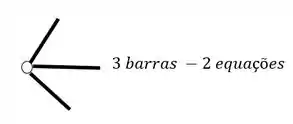
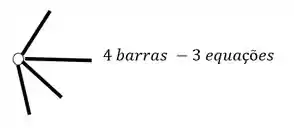
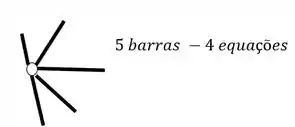
Esses dois grupos nos darão todas as equações do pórtico, mas quem nos dará as incógnitas?
Para as incógnitas nos temos 2 grupos também, um grupo é das reações de apoio, que teremos os seguintes números de incógnitas relacionadas a cada apoio
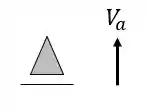
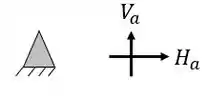
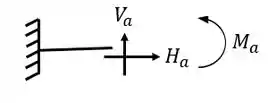
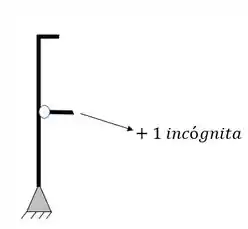
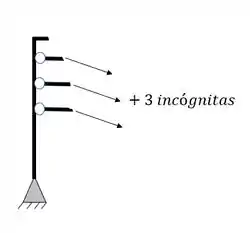
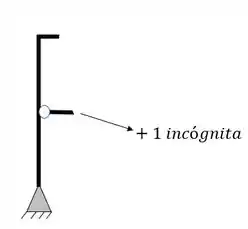
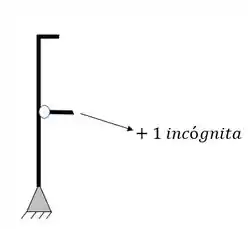
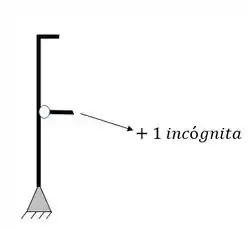
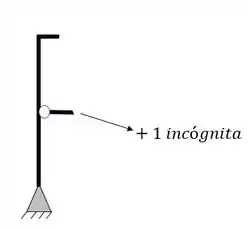
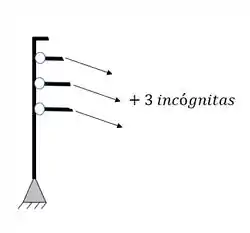
O segundo grupo de incógnitas virão dos tirantes e cabos, que somarão ao total de incógnitas mais 1 incógnita por tirante, por exemplo
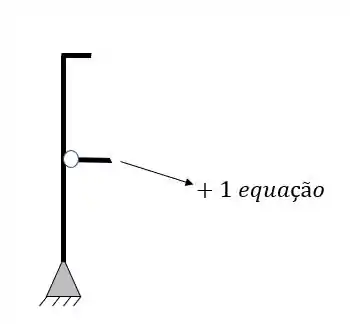
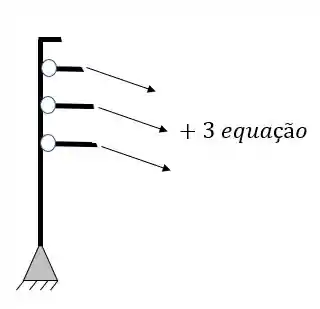
com isso temos todas as possibilidades de equações e incógnitas que podem aparecer no nosso pórtico.
O balanço de incógnitas
Pensa no seguinte, quando tivermos o numero de equações e incógnitas, nós poderemos ter três casos no pórtico simples
O primeiro caso é
Nesse caso, se tivermos pelo menos 1 vetor em cada direção, e o número de incógnitas for exatamente igual ao de equações, teremos uma estrutura isostática.
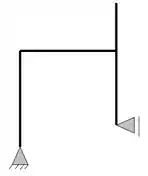
Nesse caso temos que o número de incógnitas serão 3, já que não temos tirantes nesse caso.
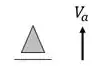
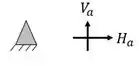
Como também não há rótulas, o número de equações serão as 3 equações de equilíbrio
como temos pelo menos um vetor em cada direção e o número de incógnitas é igual ao número de equações, falamos que essa estrutura é isostática.
O segundo caso é
Nesse caso, se tivermos pelo menos 1 vetor em cada direção, e o número de incógnitas for maior que o de equações, teremos uma estrutura, hiperestática
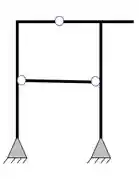
Nesse caso temos que o número de incógnitas serão 5. Quatro incógnitas dos apoios e 1 dos tirantes.
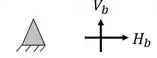
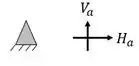
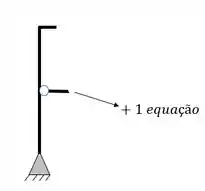
Como também há 1 rótula, o número de equações será as 3 equações de equilíbrio mais o número de equações que vem da rótula, como nesse caso só temos 2 barras na mesma rótula, teremos mais uma equação
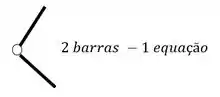
como temos pelo menos um vetor em cada direção e o número de incógnitas é maior que número de equações, falamos que essa estrutura hiperestática.
E por fim, o terceiro caso é
Nesse caso, se tivermos todos os vetores na mesma direção, ou se o número de incógnitas for menor que o número de equações, teremos uma estrutura hipostática.
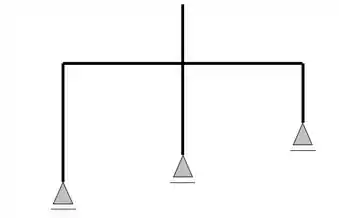
Nesse caso, se fizermos o balanço de incógnitas e de equações, veremos que temos 3 incógnitas e 3 equações, logo, você poderia dizer que é uma estrutura isostática, certo?
Errado, veja que todos os nossos apoios, apontam em uma mesma direção, ou seja, não respeitamos a regra de ter pelo menos 1 vetor em cada direção, logo, nesse caso, a nossa estrutura e hipostática.
Vale lembrar que nesse assunto só aprenderemos a resolver estruturas isostáticas, por isso é muito importante saber definir bem o tipo de estruturas que nós temos, e nesse caso, estamos definindo quando temos, primeiro, um pórtico simples, e segundo, uma estrutura isostática. É muito importante saber o seguinte, se a nossa estrutura for isostática, ela vai ser um pórtico simples ou um conjunto de pórticos simples, mas será de alguma forma, um pórtico simples.
vamos dar uma treinada com exercícios, e com isso pegar a manha dos conceitos que nos garantem conhecer o que é um pórtico ou não, vamos lá?

Equilíbrio de equações e incógnitas
O balanço de incógnitas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Faça o balanceamento de incógnitas e equações nos pórticos abaixo.
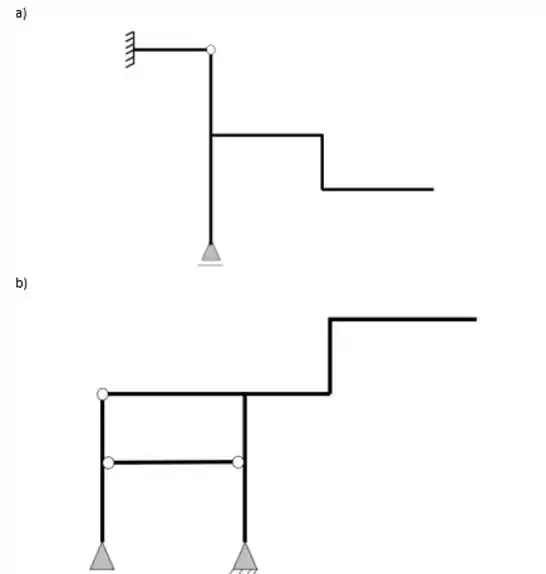
Passo 1
Vamos lá então. Sabemos que para solucionar esse tipo de problema precisamos seguir um passo a passo que irá nos ajudar nesse balanceamento, e a sequência de passos é
- Primeiro devemos fazer o balanceamento de incógnitas, e sabemos que as incógnitas são dadas pelos apoios ou por tirantes, quando esses últimos existem, e o número de incógnitas é dado da seguinte maneira:
- Em segundo lugar devemos fazer a contagem do número de equações, e ela será feita de duas maneiras, temos as 3 equações de equilíbrio que já conhecemos, e também temos a relação de equações dadas por cada rótula que aparece no nosso pórtico, em que o número de equações é dado pelo número de barras que chegam na nossa rótula, subtraído de um, e com isso podemos ver abaixo como contabilizar as nossas equações
- Por fim fazemos o equilíbrio de equações e incógnitas e verificamos qual o tipo de estruturas que temos, que respeitará uma das seguintes relações
Apoios
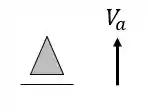
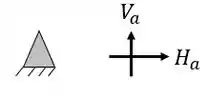
Tirantes
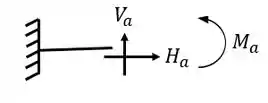
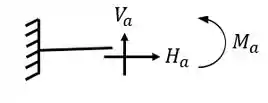
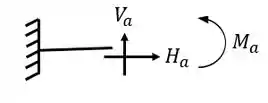
Equações de equilíbrio
Rótulas no pórtico
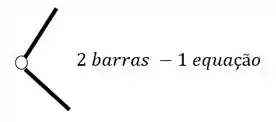
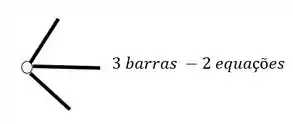
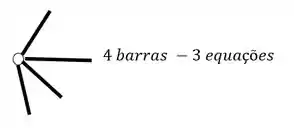
Isostático
E uma reação de apoio em cada direção
Hipostático
Ou não existe uma reação de apoio em cada direção
Hiperestático
E uma reação de apoio em cada direção
Entendido tudo isso, vamos aplicar ao nosso exercício.
Passo 2
Vamos primeiro resolver o item a) do nosso problema, e já sabemos que a primeira coisa que devemos fazer é a contabilização do número de incógnitas do nosso problema, olhando a nossa estrutura temos que
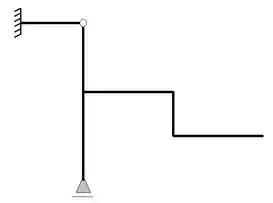
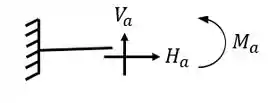
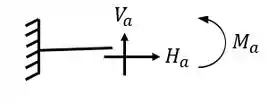
Ela possui um apoio do primeiro gênero (apenas 1 reação) e um apoio do terceiro gênero (3 reações), com isso podemos dizer que as nossas reações de apoios serão
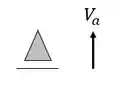
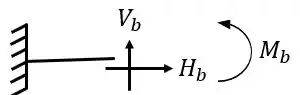
Logo, fazendo a contabilidade, podemos ver que temos ao todo 4 incógnitas no nosso problema, além do mais, nesse item a) não possuímos nenhuma corda ou tirante. Feito isso vamos ao segundo passo.
Passo 3
O segundo passo consiste em contabilizarmos o número de equações. Já sabemos de cara que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
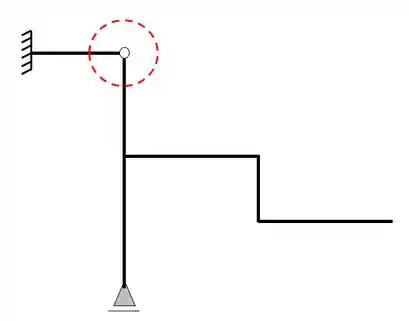
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
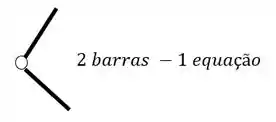
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Passo 4
Agora é simples, basta fazermos o balanceamento.
Nosso pórtico possui 4 incógnitas e 4 equações, logo podemos dizer que
E temos uma reação de apoio em cada direção
Logo a nossa estrutura de pórtico do item a) é uma estrutura do tipo isostática. Vamos agora ao item b).
Passo 5
Agora vamos resolver o item b) do nosso problema, e já sabemos que a primeira coisa que devemos fazer é a contabilização do número de incógnitas do nosso problema, olhando a nossa estrutura temos que
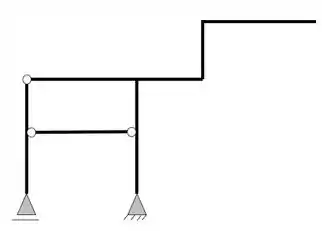
Ela possui um apoio do primeiro gênero (apenas 1 reação) e um apoio do segundo gênero (2 reações), com isso podemos dizer que as nossas reações de apoios serão
Mas não se esqueça que também temos um tirante no nosso pórtico, logo também contabilizamos ele como uma incógnita
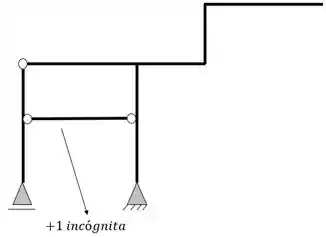
Logo, fazendo a contabilidade de incógnitas, teremos que o item b) tem 4 incógnitas ao todo, que são, 3 de apoios e 1 de tirante.
Passo 6
O segundo passo consiste em contabilizarmos o número de equações. Já sabemos de cara que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
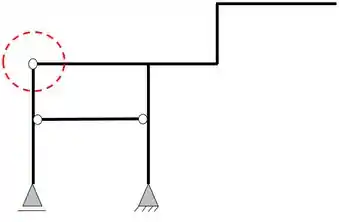
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
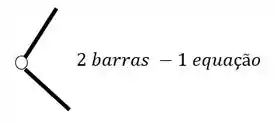
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Passo 7
Agora é simples, basta fazermos o balanceamento.
Nosso pórtico possui 4 incógnitas e 4 equações, logo podemos dizer que
E temos uma reação de apoio em cada direção
Logo a nossa estrutura de pórtico do item b) também é uma estrutura do tipo isostática.
Resposta
- Pórtico isostático com 4 incógnitas e 4 equações
- Pórtico isostático com 4 incógnitas e 4 equações
Exercício Resolvido #2
Elaboração Própria
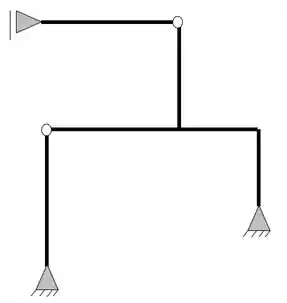
Faça o balanceamento de incógnitas e equações do pórtico abaixo.
Passo 1
Vamos lá então. Sabemos que para solucionar esse tipo de problema precisamos seguir um passo a passo que irá nos ajudar nesse balanceamento, e a sequência de passos é
- Primeiro devemos fazer o balanceamento de incógnitas, e sabemos que as incógnitas são dadas pelos apoios ou por tirantes, quando esses últimos existem, e o número de incógnitas é dado da seguinte maneira:
- Em segundo lugar devemos fazer a contagem do número de equações, e ela será feita de duas maneiras, temos as 3 equações de equilíbrio que já conhecemos, e também temos a relação de equações dadas por cada rótula que aparece no nosso pórtico, em que o número de equações é dado pelo número de barras que chegam na nossa rótula, subtraído de um, e com isso podemos ver abaixo como contabilizar as nossas equações
- Por fim fazemos o equilíbrio de equações e incógnitas e verificamos qual o tipo de estruturas que temos, que respeitará uma das seguintes relações
Apoios
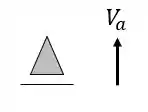
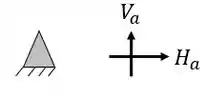
Tirantes
Equações de equilíbrio
Rótulas no pórtico
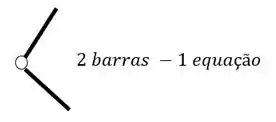
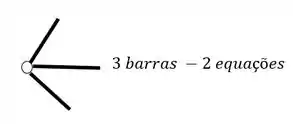
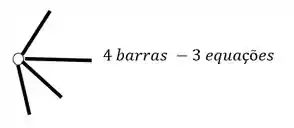
Isostático
E uma reação de apoio em cada direção
Hipostático
Ou não existe uma reação de apoio em cada direção
Hiperestático
E uma reação de apoio em cada direção
Entendido tudo isso, vamos aplicar ao nosso exercício.
Passo 2
Já sabemos que a primeira coisa que devemos fazer é a contabilização do número de incógnitas do nosso problema, olhando a nossa estrutura temos que
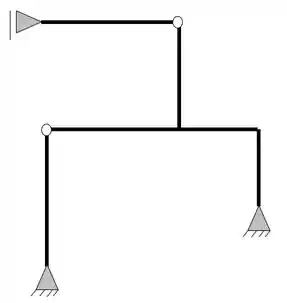
Ela possui um apoio do primeiro gênero (apenas 1 reação) e dois apoios do segundo gênero (2 reações), com isso podemos dizer que as nossas reações de apoios serão
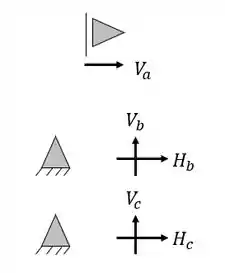
Logo, fazendo a contabilidade, podemos ver que temos ao todo 5 incógnitas no nosso problema, além do mais, não possuímos nenhuma corda ou tirante. Feito isso vamos ao segundo passo.
Passo 3
O segundo passo consiste em contabilizarmos o número de equações. Já sabemos de cara que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta duas rótulas
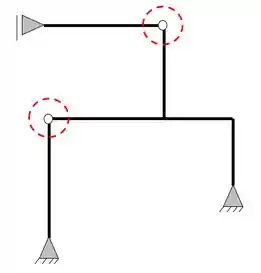
Como podemos ver, temos duas barras nessas rótulas, logo, teremos o seguinte
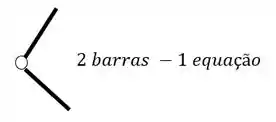
Fazendo a contabilidade, teremos um total de 5 equações, 3 de equilíbrio e 1 de cada rótula.
Passo 4
Agora é simples, basta fazermos o balanceamento.
Nosso pórtico possui 5 incógnitas e 5 equações, logo podemos dizer que
E temos uma reação de apoio em cada direção
Logo a nossa estrutura de pórtico é uma estrutura do tipo isostática.
Resposta
Pórtico isostático com 5 incógnitas e 5 equações
Exercício Resolvido #3
Elaboração Própria
Determine se o pórtico abaixo é do tipo Isostático, hiperestático ou Hipostático. Para isso use os conceitos de balanceamento de incógnitas e equações.
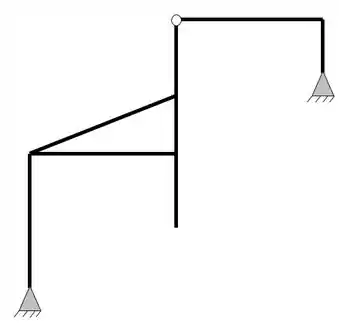
Passo 1
Vamos lá então. Sabemos que para solucionar esse tipo de problema precisamos seguir um passo a passo que irá nos ajudar nesse balanceamento, e a sequência de passos é
- Primeiro devemos fazer o balanceamento de incógnitas, e sabemos que as incógnitas são dadas pelos apoios ou por tirantes, quando esses últimos existem, e o número de incógnitas é dado da seguinte maneira:
- Em segundo lugar devemos fazer a contagem do número de equações, e ela será feita de duas maneiras, temos as 3 equações de equilíbrio que já conhecemos, e também temos a relação de equações dadas por cada rótula que aparece no nosso pórtico, em que o número de equações é dado pelo número de barras que chegam na nossa rótula, subtraído de um, e com isso podemos ver abaixo como contabilizar as nossas equações
- Por fim fazemos o equilíbrio de equações e incógnitas e verificamos qual o tipo de estruturas que temos, que respeitará uma das seguintes relações
Apoios
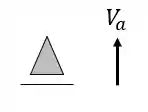
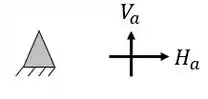
Tirantes
Equações de equilíbrio
Rótulas no pórtico
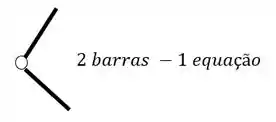
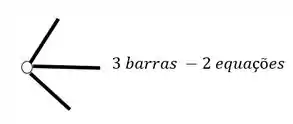
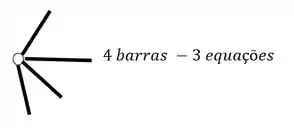
Isostático
E uma reação de apoio em cada direção
Hipostático
Ou não existe uma reação de apoio em cada direção
Hiperestático
E uma reação de apoio em cada direção
Entendido tudo isso, vamos aplicar ao nosso exercício.
Passo 2
Já sabemos que a primeira coisa que devemos fazer é a contabilização do número de incógnitas do nosso problema, olhando a nossa estrutura temos que
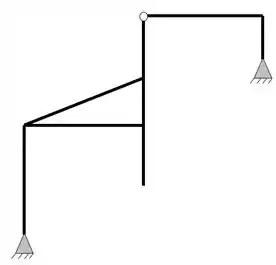
Ela possui dois apoios do segundo gênero (2 reações), com isso podemos dizer que as nossas reações de apoios serão
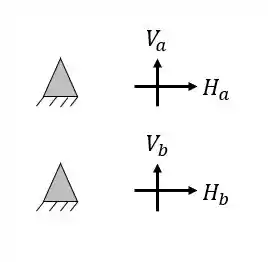
Logo, fazendo a contabilidade, podemos ver que temos ao todo 4 incógnitas no nosso problema, além do mais, não possuímos nenhuma corda ou tirante. Feito isso vamos ao segundo passo.
Passo 3
O segundo passo consiste em contabilizarmos o número de equações. Já sabemos de cara que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
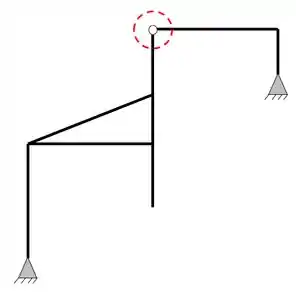
Como podemos ver, temos duas barras nessas rótulas, logo, teremos o seguinte
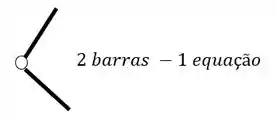
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Passo 4
Agora é simples, basta fazermos o balanceamento.
Nosso pórtico possui 4 incógnitas e 4 equações, logo podemos dizer que
E temos uma reação de apoio em cada direção
Logo a nossa estrutura de pórtico é uma estrutura do tipo isostática.
Resposta
Pórtico isostático com 4 incógnitas e 4 equações
Exercício Resolvido #4
Elaboração Própria
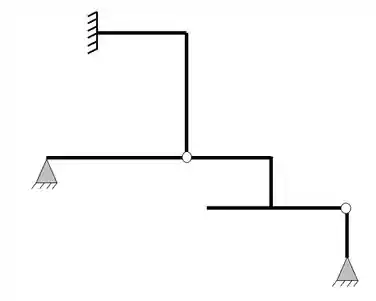
Determine se o pórtico abaixo é do tipo Isostático, hiperestático ou Hipostático. Para isso use os conceitos de balanceamento de incógnitas e equações.
Passo 1
Vamos lá então. Sabemos que para solucionar esse tipo de problema precisamos seguir um passo a passo que irá nos ajudar nesse balanceamento, e a sequência de passos é
- Primeiro devemos fazer o balanceamento de incógnitas, e sabemos que as incógnitas são dadas pelos apoios ou por tirantes, quando esses últimos existem, e o número de incógnitas é dado da seguinte maneira:
- Em segundo lugar devemos fazer a contagem do número de equações, e ela será feita de duas maneiras, temos as 3 equações de equilíbrio que já conhecemos, e também temos a relação de equações dadas por cada rótula que aparece no nosso pórtico, em que o número de equações é dado pelo número de barras que chegam na nossa rótula, subtraído de um, e com isso podemos ver abaixo como contabilizar as nossas equações
- Por fim fazemos o equilíbrio de equações e incógnitas e verificamos qual o tipo de estruturas que temos, que respeitará uma das seguintes relações
Apoios
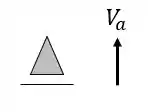
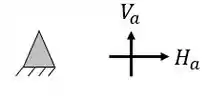
Tirantes
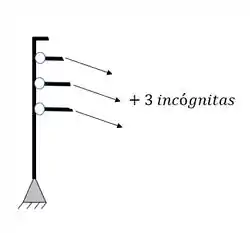
Equações de equilíbrio
Rótulas no pórtico
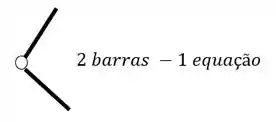
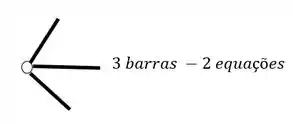
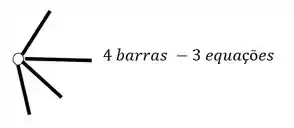
Isostático
E uma reação de apoio em cada direção
Hipostático
Ou não existe uma reação de apoio em cada direção
Hiperestático
E uma reação de apoio em cada direção
Entendido tudo isso, vamos aplicar ao nosso exercício.
Passo 2
Já sabemos que a primeira coisa que devemos fazer é a contabilização do número de incógnitas do nosso problema, olhando a nossa estrutura temos que
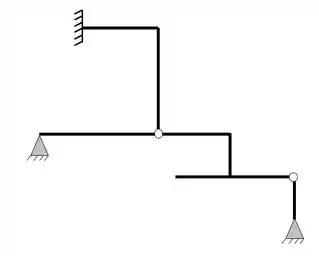
Ela possui um apoio do terceiro gênero (3 reações) e dois apoios do segundo gênero (2 reações), com isso podemos dizer que as nossas reações de apoios serão
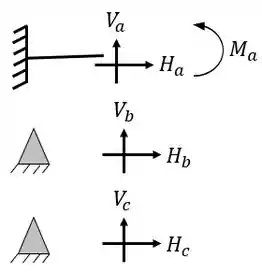
Logo, fazendo a contabilidade, podemos ver que temos ao todo 7 incógnitas no nosso problema, além do mais, não possuímos nenhuma corda ou tirante. Feito isso vamos ao segundo passo.
Passo 3
O segundo passo consiste em contabilizarmos o número de equações. Já sabemos de cara que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta duas rótulas
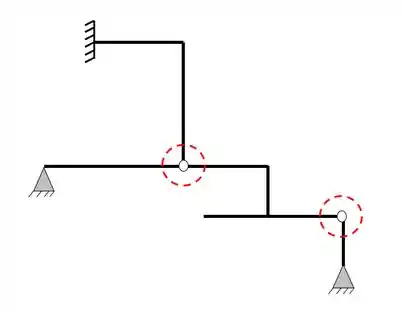
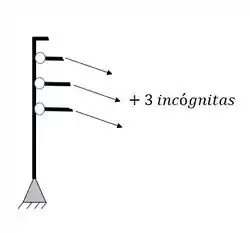
Como podemos ver, temos duas barras em uma rótula e três barras na outra rótula, logo, teremos o seguinte
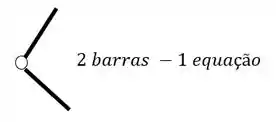
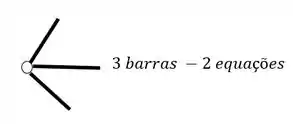
Fazendo a contabilidade, teremos um total de 6 equações, 3 de equilíbrio e 1 de uma rótula e 2 da outra rótula.
Passo 4
Agora é simples, basta fazermos o balanceamento.
Nosso pórtico possui 7 incógnitas e 6 equações, logo podemos dizer que
E temos uma reação de apoio em cada direção
Logo a nossa estrutura de pórtico é uma estrutura do tipo hiperestática.
Resposta
Pórtico hiperestático com 7 incógnitas e 6 equações
Exercício Resolvido #5
Elaboração Própria
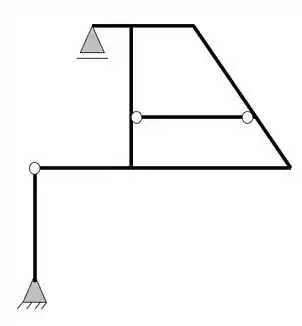
Determine se o pórtico abaixo é do tipo Isostático, hiperestático ou Hipostático. Para isso use os conceitos de balanceamento de incógnitas e equações.
Passo 1
Vamos lá então. Sabemos que para solucionar esse tipo de problema precisamos seguir um passo a passo que irá nos ajudar nesse balanceamento, e a sequência de passos é
- Primeiro devemos fazer o balanceamento de incógnitas, e sabemos que as incógnitas são dadas pelos apoios ou por tirantes, quando esses últimos existem, e o número de incógnitas é dado da seguinte maneira:
- Em segundo lugar devemos fazer a contagem do número de equações, e ela será feita de duas maneiras, temos as 3 equações de equilíbrio que já conhecemos, e também temos a relação de equações dadas por cada rótula que aparece no nosso pórtico, em que o número de equações é dado pelo número de barras que chegam na nossa rótula, subtraído de um, e com isso podemos ver abaixo como contabilizar as nossas equações
- Por fim fazemos o equilíbrio de equações e incógnitas e verificamos qual o tipo de estruturas que temos, que respeitará uma das seguintes relações
Apoios
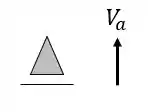
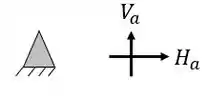
Tirantes
Equações de equilíbrio
Rótulas no pórtico
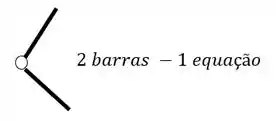
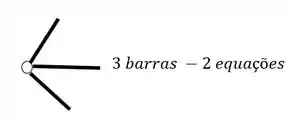
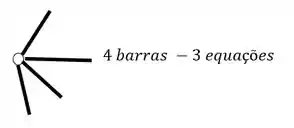
Isostático
E uma reação de apoio em cada direção
Hipostático
Ou não existe uma reação de apoio em cada direção
Hiperestático
E uma reação de apoio em cada direção
Entendido tudo isso, vamos aplicar ao nosso exercício.
Passo 2
Já sabemos que a primeira coisa que devemos fazer é a contabilização do número de incógnitas do nosso problema, olhando a nossa estrutura temos que
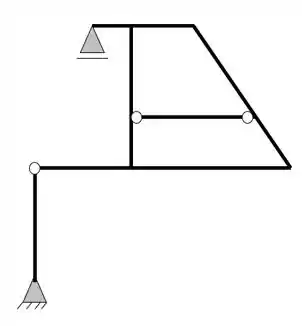
Ela possui um apoio do primeiro gênero (apenas 1 reação) e um apoio do segundo gênero (2 reações), com isso podemos dizer que as nossas reações de apoios serão
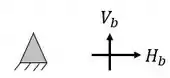
Mas não se esqueça que também temos um tirante no nosso pórtico, logo também contabilizamos ele como uma incógnita
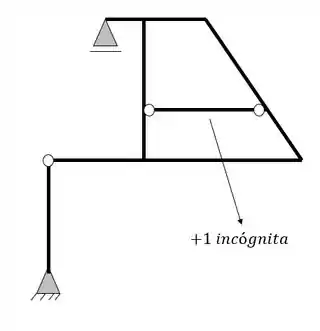
Logo, fazendo a contabilidade de incógnitas, teremos 4 incógnitas ao todo, que são, 3 de apoios e 1 de tirante.
Passo 3
O segundo passo consiste em contabilizarmos o número de equações. Já sabemos de cara que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
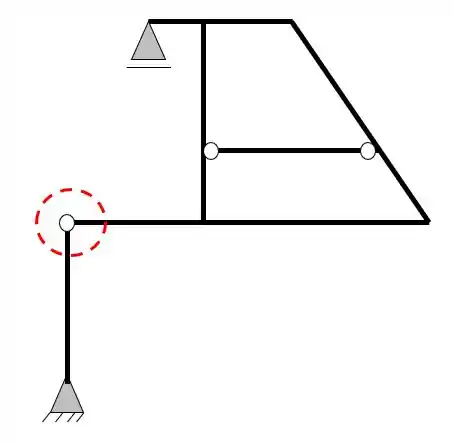
Como podemos ver, temos duas barras em uma rótula, logo, teremos o seguinte
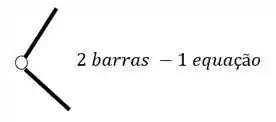
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 de uma rótula.
Passo 4
Agora é simples, basta fazermos o balanceamento.
Nosso pórtico possui 4 incógnitas e 4 equações, logo podemos dizer que
E temos uma reação de apoio em cada direção
Logo a nossa estrutura de pórtico é uma estrutura do tipo isostática.
Resposta
Pórtico isostático com 4 incógnitas e 4 equações