Solução de Vigas Simples
Produzido por Pablo RicardoTeoria
Introdução
Nessa aula, queremos mostrar uma nova forma de solução de vigas, para encontrarmos as equações a partir de integrais. No caso vamos ver uma situação e a partir dessa situação vamos aprender a calcular tanto as fórmulas quanto comparar os métodos de solução.
Vale destacar que se o seu professor não obriga a resolver dessa maneira e você se sente mais confortável resolvendo por equilíbrio, essa aula não vai te ajudar muito. Mas se o seu professor obriga você a fazer por esse método, ou você quer aprender outras formas de resolver, vamos partir para nossa situação para entendermos essa nova forma de descobrir os diagramas, bora lá?

Equação da carga aplicada
Para isso, temos que analisar o seguinte, a nossa carga aplicada possui uma equação, que sempre consideraremos com o sinal contrário, ou seja
Por exemplo, imagine que tenhamos a seguinte carga distribuída
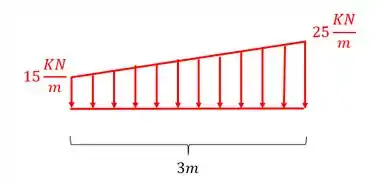
Qual a equação dessa carga distribuída?
Basta usarmos a equação da reta
Em que sabemos que quando
E que quando
Substituindo teremos o seguinte sistema
Resolvendo o sistema encontramos que
Logo nossa equação será
Mas lembre-se que devemos definir a nossa carga com sinal contrário, logo
Para outros carregamentos temos que


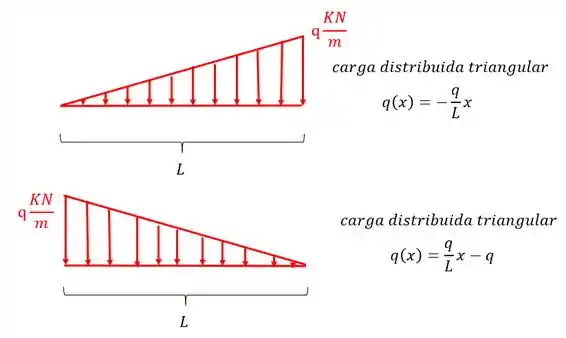
Equação do Cortante e do Momento Fletor
Definido a carga podemos definir a fórmula do cortante e do momento fletor, que são dadas por
- Cortante
- Momento Fletor
- Cortante
- Momento fletor
Vale ressaltar que as constantes e serão determinadas pelas condições de contorno, que geralmente dependem dos apoios ou do ponto da barra que estivermos calculando.
Para entender essas fórmulas vamos fazer um exemplo bem completinho pra pegarmos bem esses macetes.
Situação
Imagine que seu professor coloque na prova a seguinte questão, pedindo as equações de momentos fletores e cortantes
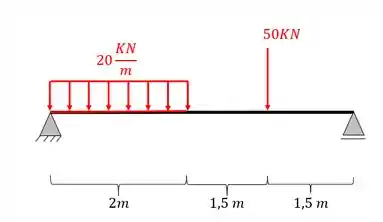
Como começar a fazer isso?

Separação dos intervalos
Os pontos que marcam as separações dos intervalos são os pontos em que a mudança de carga brusca, por exemplo, para o nosso exercício, os pontos com mudança de carga são
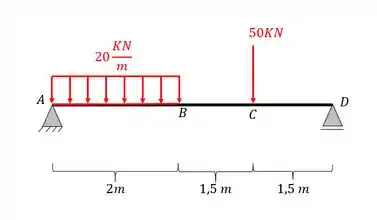
Com isso já sabemos que precisamos calcular as equações para 3 intervalos, AB, BC e CD. Como cada intervalo tem 2 equações (cortante e momento fletor), no fim deveremos ter 6 equações. Vamos para o próximo passo.
Reações de apoio
Sabemos que o nosso diagrama de corpo livre será
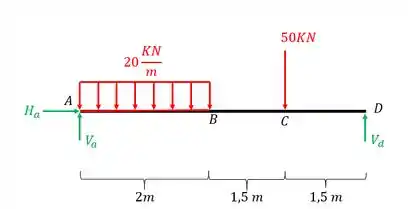
Sabemos que pelas equações de equilíbrio teremos
Se já temos os intervalos e já temos as reações de apoio, agora é só calcular as equações.
Equações trecho AB
Como a gente viu, temos que determinar as equações das cargas, sabemos que no trecho AB temos apenas carga distribuída, e essa carga é constante, logo teremos
Para equação do cortante termos que
Perceba que o trecho AB é definido pelo intervalo [0 ; 2]. Se conhecermos o valor do cortante em qualquer ponto desse intervalo, nós descobrimos facilmente o valor do .
Nesse caso, sabemos que o ponto 0 é onde está o apoio. E nesse caso, o cortante no ponto zero é a própria reação de apoio, tomando cuidado com o sinal, que é dado por
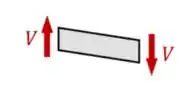
que significa que o cortante é positivo pela esquerda se o vetor for pra cima, ou é positivo pela direita se o vetor for pra baixo. Como nesse caso a reação de apoio está do lado esquerdo e pra cima, o nosso cortante é positivo, com valor igual a
Substituindo na nossa equação teremos
Logo a equação do cortante é
Pra equação do momento fletor temos
Nesse caso, vamos tomar novamente o momento no ponto x=0, que nesse caso, é zero mesmo, já que temos um apoio do segundo gênero, dessa forma teremos
E a equação do momento fletor será
Equações trecho BC
O trecho BC é definido no intervalo de [2 ; 3,5]. Perceba que todos os valores do ponto a 2m podem ser definidos pela equação do trecho anterior. Vamos logo definir esses valores então
Agora precisamos ver o carregamento, podemos dizer que se fossemos considerar um carregamento seria apenas o carregamento concentrado de 50, então teríamos que
Logo a equação do cortante será
Qual vai ser o valor de ?
Muito simples, só precisamos de um ponto do trecho BC, e temos exatamente o ponto B calculado ali em cima, então é só substituir
Logo o cortante será
E o momento fletor?
Só jogar na outra fórmula
E qual será o valor do momento? É só usar o valor que calculamos para o ponto B ali em cima
Logo o momento fletor será
Equações trecho CD
A equação pro trecho CD, seguirá o mesmo principio que seguimos no trecho BC, ou seja, vamos calcular os valores de cortante e fletor do ponto C, que está a 3,5m do primeiro apoio
Agora precisamos ver o carregamento, podemos dizer que se fossemos considerar um carregamento seria apenas o carregamento concentrado de 50, como fizemos no caso anterior , então teríamos que
Logo a equação do cortante será
Qual vai ser o valor de ?
Muito simples, só precisamos de um ponto do trecho BC, e temos exatamente o ponto C calculado ali em cima, então é só substituir, tomando cuidado que no ponto C que estamos olhando tem uma carga concentrada de -50 KN. Porque negativo? Porque quando olhamos essa carga pela esquerda ela é para baixo, ao contrario do nosso sinal usual, por isso, consideramos ela negativa, dessa forma teremos
Logo o cortante será
E o momento fletor?
Só jogar na outra fórmula
E qual será o valor do momento? É só usar o valor que calculamos para o ponto C ali em cima, e nesse caso a carga de 50 não precisa ser considerada pois ela já está sendo considerada no cortante que vamos substituir
Logo o momento fletor será
Ou seja, no final as equações serão

Com essas equações conseguimos facilmente determinar o diagrama de cortante e momentos fletores, porém, como já foi dito no início, se o método usado fosse o equilíbrio da barra, chegaríamos nas mesmas equações, tanto o método de integrais quanto o método de equilíbrio dariam a mesma resposta, tanto é que podemos confirmar isso para o trecho CD apenas para mostrar que de fato ambos os métodos dão os mesmos valores.
Equações trecho CD (pelo método de equilíbrio)
Cortando a barra no trecho CD teríamos
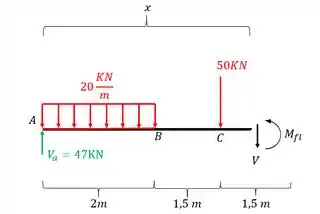
Equilibrando o cortante teremos
Equilibrando o Momento fletor teremos
Ou seja, de fato tanto por um método quanto por outro chegamos nos mesmos valores, então fica a seu critério escolher a melhor forma de resolver o problema 😊.
Diagrama de cortante e momento fletor
Agora que já temos as equações, basta desenhar os diagramas. Nesse caso usamos o programa ftool pra fazer os gráficos bem bonitos pra vocês, e vale ressaltar que nesse caso consideramos o momento fletor positivo pra baixo e negativo pra cima, e o cortante positivo pra cima e negativo pra baixo. Pra fica fácil pra lembrar do fletor, sempre desenhamos os gráficos na direção das fibras tracionadas, quando as fibras tracionadas estão em baixo, é positivo, quando as fibras tracionadas estão em cima, negativo, com isso o nosso diagrama fica
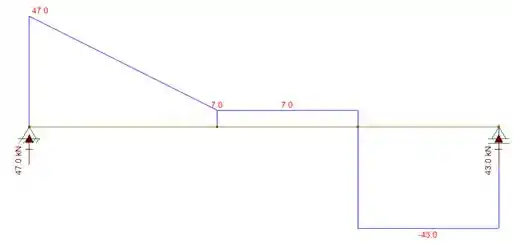
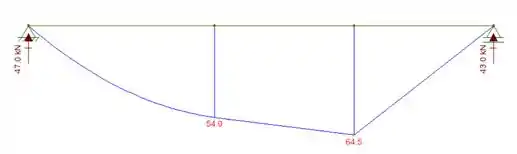
Bem bonito né? Perceba que onde está parabólico é exatamente no trecho que a equação é do segundo grau, e onde está retilíneo é onde a equação é do primeiro grau, assim como os trechos constantes.
Agora é treinar mais e pegar todos os macetes, bora fazer exercício?

Equação do Cortante e do Momento Fletor
Situação
Separação dos intervalos
Reações de apoio
Equações trecho AB
Equações trecho BC
Equações trecho CD
Equações trecho CD (pelo método de equilíbrio)
Diagrama de cortante e momento fletor
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Calcule as reações de apoio da viga dada abaixo.
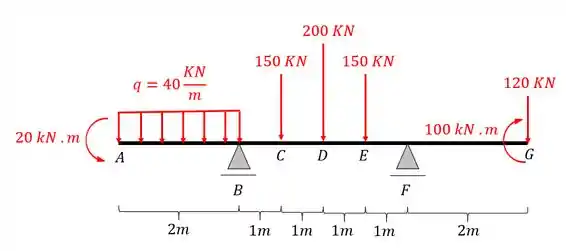
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequência de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o último passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
Dito tudo isso, vamos pôr a mão na massa!!!
Passo 2
Como vimos, o objetivo da nossa questão são apenas as reações de apoio, por isso, iremos até o passo 2 que vimos acima. Um macete legal é trocarmos todas as cargas distribuídas que tivermos no nosso enunciado por cargas concentradas, no nosso caso temos apenas uma carga do tipo retangular, e nesse caso teremos que o nosso vetor concentrado que representa o distribuído será
Assim
Dessa forma o nosso carregamento ficará da seguinte maneira na estrutura
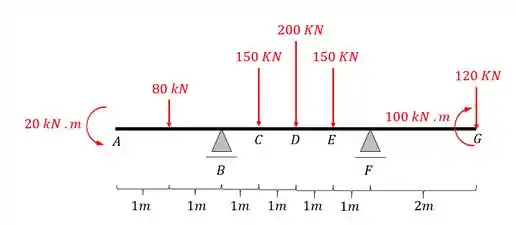
Passo 3
Agora que já determinamos os trechos e a equação, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, usando as equações de equilíbrio e definindo o diagrama de corpo livre, teremos
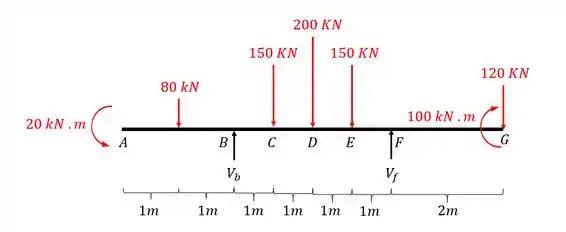
Perceba que trocamos os apoios por reações de apoio
E assim calculamos as nossas reações de apoio.
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule as reações de apoio da viga dada abaixo.
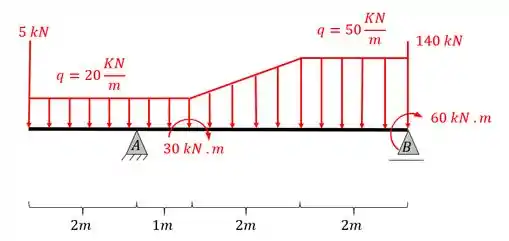
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequência de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o último passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
Dito tudo isso, vamos pôr a mão na massa!!!
Passo 2
Como vimos, o objetivo da nossa questão são apenas as reações de apoio, por isso, iremos até o passo 2 que vimos acima. Um macete legal é trocarmos todas as cargas distribuídas que tivermos no nosso enunciado por cargas concentradas, no nosso caso temos apenas uma carga do tipo retangular, e nesse caso teremos que o nosso vetor concentrado que representa o distribuído será
Assim
O trapezoidal vamos dividir em duas regiões
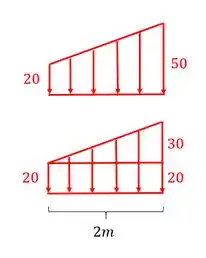
A parte retangular inferior será
A parte triangular será
E no triangular a distancia do lado zero do triangulo será 2/3 do vão
Dessa forma o nosso carregamento ficará da seguinte maneira na estrutura
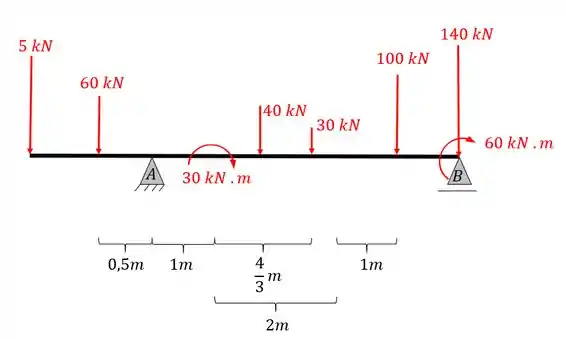
Passo 3
Agora que já determinamos os trechos e a equação, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, usando as equações de equilíbrio e definindo o diagrama de corpo livre, teremos
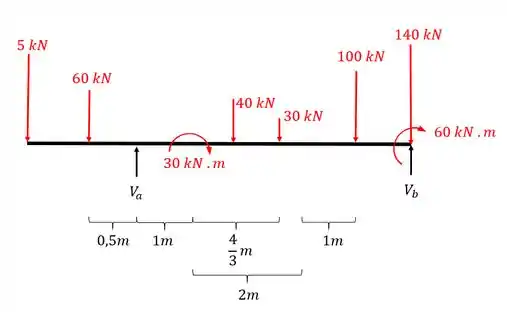
Perceba que trocamos os apoios por reações de apoio
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule as reações de apoio da viga dada abaixo.
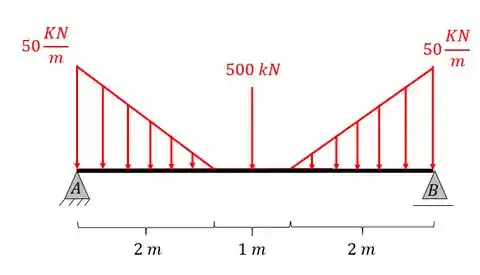
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequência de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o último passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
Dito tudo isso, vamos pôr a mão na massa!!!
Passo 2
Como vimos, o objetivo da nossa questão são apenas as reações de apoio, por isso, iremos até o passo 2 que vimos acima. Um macete legal é trocarmos todas as cargas distribuídas que tivermos no nosso enunciado por cargas concentradas, no nosso caso temos apenas uma carga do tipo retangular, e nesse caso teremos que o nosso vetor concentrado que representa o distribuído será
Assim
E no triangular a distância do maior lado do triangulo será 1/3 do vão
Dessa forma o nosso carregamento ficará da seguinte maneira na estrutura
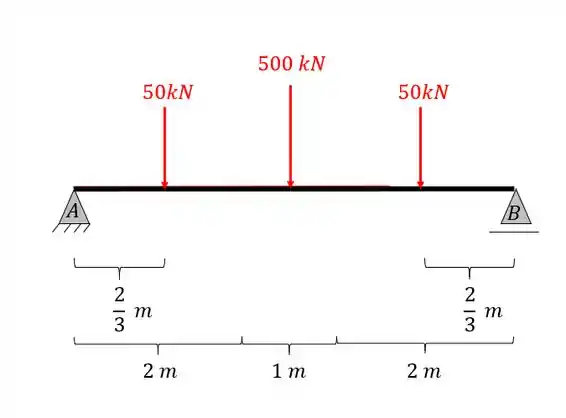
Passo 3
Agora que já determinamos os trechos e a equação, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, usando as equações de equilíbrio e definindo o diagrama de corpo livre, teremos
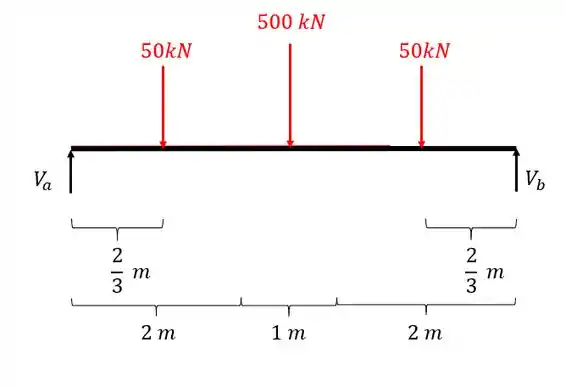
Perceba que trocamos os apoios por reações de apoio
Resposta
Exercício Resolvido #4
Elaboração Própria
Calcule as reações de apoio da viga dada abaixo.
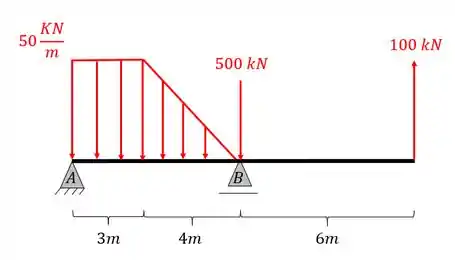
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequência de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o último passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
Dito tudo isso, vamos pôr a mão na massa!!!
Passo 2
Como vimos, o objetivo da nossa questão são apenas as reações de apoio, por isso, iremos até o passo 2 que vimos acima. Um macete legal é trocarmos todas as cargas distribuídas que tivermos no nosso enunciado por cargas concentradas, no nosso caso temos apenas uma carga do tipo retangular, e nesse caso teremos que o nosso vetor concentrado que representa o distribuído será
Assim
E no triangular a distância do lado maior do triangulo será 1/3 do vão
Dessa forma o nosso carregamento ficará da seguinte maneira na estrutura
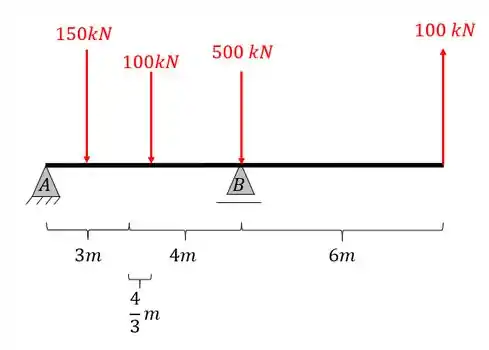
Passo 3
Agora que já determinamos os trechos e a equação, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, usando as equações de equilíbrio e definindo o diagrama de corpo livre, teremos
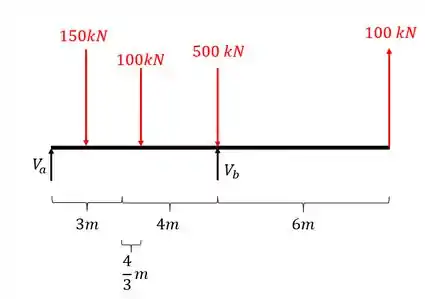
Perceba que trocamos os apoios por reações de apoio
Resposta
Exercício Resolvido #5
Elaboração Própria
Determine as equações de cortante e momento fletor da viga simples dada abaixo, com carregamento triangular. Não se esqueça de analisar as características pertinentes a carregamentos triangulares.
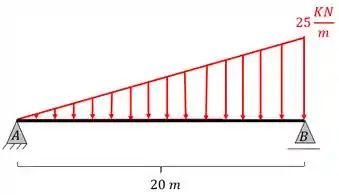
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequência de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o último passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
Dito tudo isso, vamos pôr a mão na massa!!!
Passo 2
Já temos um trecho, que nesse caso é o trecho AB. Podemos observar que dentro do trecho AB não há sub trechos, já que estamos apenas no trecho triangular e não há nem apoio e nem cargas concentradas nesse trecho, com isso já executamos a primeira parte do nosso passo a passo.
Antes de determinamos as reações de apoio vamos montar uma equação que compatibilize com o carregamento do trecho AB, dessa forma, imagine que colocamos o nosso triângulo em um plano cartesiano.
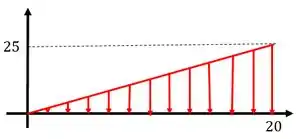
Agora é só determinar a equação da reta, usando a equação
Substituindo os nossos dados teremos
Resolvendo o sistema teremos
Logo a nossa equação será
Passo 3
Agora que já determinamos os trechos e a equação, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, usando as equações de equilíbrio e definindo o diagrama de corpo livre, teremos
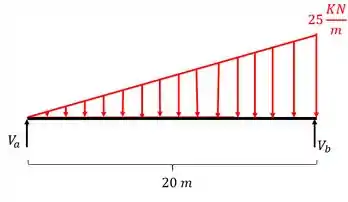
Vale relembrar que em carregamentos triangulares a resultante fica a 2/3 da base com relação ao menor lado ou a 1/3 da base em relação ao maior lado, é muito importante lembrar disso na hora de fazer a conta, pois irá influenciar no cálculo do momento fletor.
- Trecho AB
- X=0
- X=0
E assim terminamos o nosso segundo passo
Passo 4
Já sabemos a equação do nosso carregamento, definimos ele no nosso passo 2, mas para integração precisamos tomar muito cuidado, porque precisamos trocar o sinal do nosso carregamento, dessa forma, teremos que
Não se esqueça que sempre definimos a nossa carga com o sinal contrário para podermos fazer a integração.
Com isso já podemos ira pra o passo de determinação das equações, fazendo para cada trecho teremos,
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso ponto A, logo o nosso cortante nesse ponto é a própria reação de apoio em A. que nesse caso está para cima, e sempre que fizemos uma análise vindo pela esquerda com o vetor para cima ele será positivo.
Substituindo na nossa equação teremos
Com isso a nossa equação do cortante será
Para calcular o momento fletor teremos que usar a outra fórmula, com isso teremos
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso apoio A, logo o nosso momento fletor nesse ponto é zero, já que nosso apoio é do segundo gênero, e definiremos como positivo todos os momentos que tracionarem as fibras da parte de baixo, e negativo todos os vetores que estiverem tracionando as fibras da parte de cima,
Substituindo na nossa equação teremos
Com isso a nossa equação do momento fletor será
Com isso atendemos os pedidos do nosso enunciado, descobrindo as equações do trecho AB assim como as extremidades desse trecho. Agora é só ficar tranquilo pra poder integrar os trechos que forem necessários e treinar mais um pouco, beleza, vamos aos exercícios então.
Resposta
Equações trecho AB
Cortante
Momento fletor
Exercício Resolvido #6
Elaboração Própria
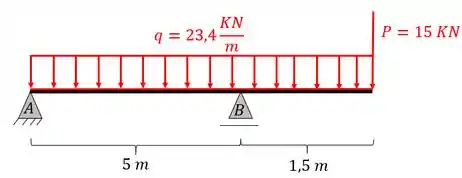
Para a viga abaixo, determine as equações de cortante e de momento fletor para cada trecho a partir da fórmula de integração. Defina os intervalos de cálculos assim como as equações usadas.
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequencia de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o ultimo passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
- Primeiro olhamos a barra apenas com a carga distribuída
- Reação de apoio em A
- Reação de apoio em B
- Carga concentrada na extremidade
Dito tudo isso, vamos por a mão na massa!!!
Passo 2
Vemos que o primeiro passo está definido como definição dos trechos em que temos que definir as equações, como faremos isso de maneira simples? Basta seguir o seguinte
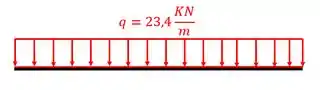
depois pensamos no seguinte, onde tem mudança brusca de esforço na barra? Nesse caso temos 3 posições:
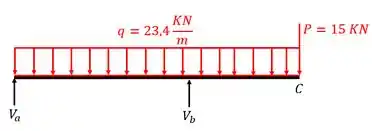
Perceba que apesar de o apoio A ser do segundo gênero, temos apenas carregamentos na vertical, o que nos permite desprezar esforços horizontais.
Como já definimos os pontos de mudanças conseguimos definir os trechos.
Logo teremos que definir as equações nos trechos AB e BC, sendo o ponto C a extremidade da barra com a carga concentrada.
Passo 2
Agora que já determinamos os trechos, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, perceba que no passo anterior já definimos o nosso diagrama de corpo livre, analisando ele pelas medidas do enunciado e juntamente usando as equações de equilíbrio, teremos
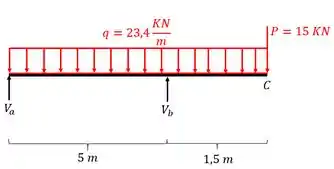
- Trecho AB
- Trecho BC
E assim terminamos o nosso segundo passo
Passo 4
Definida as nossas reações de apoio, precisamos definir a equação do nosso carregamento, veja que nesse caso tanto para o trecho AB quanto para o trecho BC o nosso carregamento distribuído é constante, logo podemos definir que a equação do nosso carregamento por todo o eixo da barra é dado por
Não se esqueça que sempre definimos a nossa carga com o sinal contrario para podermos fazer a integração.
Com isso já podemos ira pra o passo de determinação das equações, fazendo para cada trecho teremos,
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso apoio A, logo o nosso cortante nesse ponto é a reação em A que é dada por
Substituindo na nossa equação teremos que
Logo a nossa equação do cortante será
Para calcular o momento fletor teremos que usar a outra fórmula, com isso teremos
Perceba que nesse caso temos que em , o nosso momento fletor é nulo, já que representa um apoio do segundo gênero, dessa forma, usando as condições de contorno agora descoberta, teremos que
Dessa forma a nossa equação será
Para esse trecho temos o mesmo carregamento distribuído, usando a fórmula teremos
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso apoio B, logo o nosso cortante nesse ponto é o resultado da equação do trecho AB com x=5, levando em conta a reação de apoio em B, ou seja, a nossa condição de contorno será
Mas como eu disse, para o trecho AB ainda temos que considerar a sua reação de apoio, dessa forma teremos
Substituindo na nossa equação teremos que
Logo a nossa equação do cortante será
Para calcular o momento fletor teremos que usar a outra fórmula, com isso teremos
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso apoio B, logo o nosso momento fletor nesse ponto é o resultado da equação do trecho AB com x=5, nesse caso não precisamos levar em conta a reação de apoio em B, já que ela não produz momento fletor, com isso, a nossa condição de contorno será
Sabendo disso basta que substituamos isso na nossa equação, e teremos que
Dessa forma a nossa equação será
Com isso atendemos os pedidos do nosso enunciado, descobrindo as equações de cada trecho assim como as extremidades de cada trecho, viu como é tranquilo? Só é um pouco trabalhoso, mas com mais exercícios a gente paga os macetes. Vamos treinar mais? Vamos para o próximo exercício então.
Resposta
Equações trecho AB
Cortante
Momento fletor
Equações trecho BC
Cortante
Momento fletor
Exercício Resolvido #7
Elaboração Própria
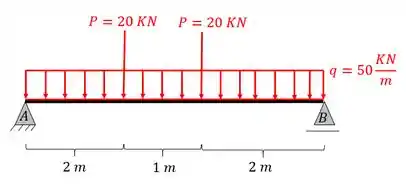
Para a viga abaixo, determine as equações de cortante e de momento fletor para cada trecho a partir da fórmula de integração. Defina os intervalos de cálculos assim como as equações usadas.
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequência de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o último passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
- Primeiro olhamos a barra apenas com a carga distribuída
- Reação de apoio em A
- Reação de apoio em B
- Carga concentrada próximo ao apoio A
- Carga concentrada próximo ao apoio B
Dito tudo isso, vamos pôr a mão na massa!!!
Passo 2
Vemos que o primeiro passo está definido como definição dos trechos em que temos que definir as equações, como faremos isso de maneira simples? Basta seguir o seguinte

depois pensamos no seguinte, onde tem mudança brusca de esforço na barra? Nesse caso temos 4 posições:
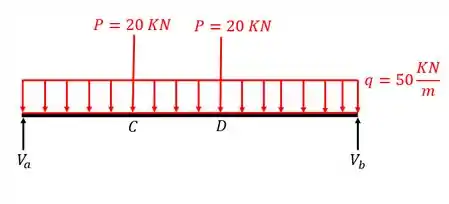
Perceba que apesar de o apoio A ser do segundo gênero, temos apenas carregamentos na vertical, o que nos permite desprezar esforços horizontais.
Como já definimos os pontos de mudanças conseguimos definir os trechos.
Logo teremos que definir as equações nos trechos AC, CD e DB.
Passo 2
Agora que já determinamos os trechos, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, perceba que no passo anterior já definimos o nosso diagrama de corpo livre, analisando ele pelas medidas do enunciado e juntamente usando as equações de equilíbrio, teremos
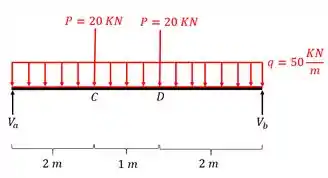
- Trecho AC
- Trecho CD
- Trecho DB
E assim terminamos o nosso segundo passo
Passo 4
Definida as nossas reações de apoio, precisamos definir a equação do nosso carregamento, veja que nesse caso tanto para o trecho AC quanto para o trecho CD quando para o trecho DB o nosso carregamento distribuído é constante, logo podemos definir que a equação do nosso carregamento por todo o eixo da barra é dado por
Não se esqueça que sempre definimos a nossa carga com o sinal contrário para podermos fazer a integração.
Com isso já podemos ira pra o passo de determinação das equações, fazendo para cada trecho teremos,
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso apoio A, logo o nosso cortante nesse ponto é a reação em A que é dada por
Substituindo na nossa equação teremos que
Logo a nossa equação do cortante será
Para calcular o momento fletor teremos que usar a outra fórmula, com isso teremos
Perceba que nesse caso temos que em , o nosso momento fletor é nulo, já que representa um apoio do segundo gênero, dessa forma, usando as condições de contorno agora descoberta, teremos que
Dessa forma a nossa equação será
Para esse trecho temos o mesmo carregamento distribuído, usando a fórmula teremos
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso ponto C, logo o nosso cortante nesse ponto é o resultado da equação do trecho AC com x=2, levando em conta o carregamento em C, ou seja, a nossa condição de contorno será
Mas como eu disse, para o trecho AC ainda temos que considerar o carregamento de 20KN concentrado, dessa forma teremos
OBS:. Perceba que usamos pois quando fazemos a análise de carregamentos, sempre que analisarmos a barra vindo pela esquerda e o carregamento for para baixo, será negativo, sempre que for para cima será positivo. Quando viermos pela direita será o contrário, para baixo será positivo e para cima negativo. Fique bem atento aos sinais para não errar de bobeira.
Substituindo na nossa equação teremos que
Logo a nossa equação do cortante será
Para calcular o momento fletor teremos que usar a outra fórmula, com isso teremos
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso ponto C, logo o nosso momento fletor nesse ponto é o resultado da equação do trecho AC com x=2, nesse caso não precisamos levar em conta o carregamento em C, já que ele não produz momento fletor, ou seja, a nossa condição de contorno será
Sabendo disso basta que substituamos isso na nossa equação, e teremos que
Dessa forma a nossa equação será
Para esse trecho temos o mesmo carregamento distribuído, usando a fórmula teremos
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso ponto D, logo o nosso cortante nesse ponto é o resultado da equação do trecho CD com x=3, levando em conta o carregamento em D, ou seja, a nossa condição de contorno será
Mas como eu disse, para o trecho CD ainda temos que considerar o carregamento de 20KN concentrado, dessa forma teremos
OBS:. Perceba que usamos pois quando fazemos a análise de carregamentos, sempre que analisarmos a barra vindo pela esquerda e o carregamento for para baixo, será negativo, sempre que for para cima será positivo. Quando viermos pela direita será o contrário, para baixo será positivo e para cima negativo. Fique bem atento aos sinais para não errar de bobeira.
Substituindo na nossa equação teremos que
Logo a nossa equação do cortante será
Para calcular o momento fletor teremos que usar a outra fórmula, com isso teremos
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso ponto D, logo o nosso momento fletor nesse ponto é o resultado da equação do trecho CD com x=3, nesse caso não precisamos levar em conta o carregamento em D, já que ele não produz momento fletor, ou seja, a nossa condição de contorno será
Sabendo disso basta que substituamos isso na nossa equação, e teremos que
Dessa forma a nossa equação será
Com isso atendemos os pedidos do nosso enunciado, descobrindo as equações de cada trecho assim como as extremidades de cada trecho, viu como é tranquilo? Só é um pouco trabalhoso, mas com mais exercícios a gente paga os macetes. Vamos treinar mais? Vamos para o próximo exercício então.
Resposta
Equações trecho AC
Cortante
Momento fletor
Equações trecho CD
Cortante
Momento fletor
Equações trecho DB
Cortante
Momento fletor
Exercício Resolvido #8
Elaboração Própria
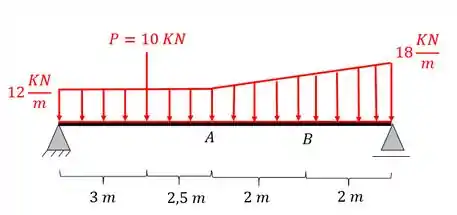
A viga abaixo está sujeita a um carregamento retangular e trapezoidal uniforme. Com base em seus conhecimentos de estruturas determine a equação do cortante e do momento fletor no trecho AB da viga.
Dica expert: Determine as condições de contorno através do diagrama de corpo livre, e não calculando as equações dos trechos anteriores ao trecho AB
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequência de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o último passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
Dito tudo isso, vamos pôr a mão na massa!!!
Passo 2
Já temos um trecho, que nesse caso é o trecho AB. Podemos observar que dentro do trecho AB não há sub trechos, já que estamos apenas no trecho trapezoidal e não há nem apoio e nem cargas concentradas nesse trecho, com isso já executamos a primeira parte do nosso passo a passo.
Antes de determinamos as reações de apoio vamos montar uma equação que compatibilize com o carregamento do trecho AB, dessa forma, imagine que colocamos o nosso trapézio em um plano cartesiano.
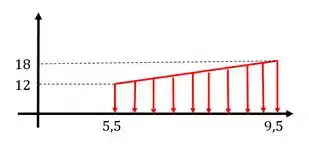
Agora é só determinar a equação da reta, usando a equação
Substituindo os nossos dados teremos
Resolvendo o sistema teremos
Logo a nossa equação será
Passo 3
Agora que já determinamos os trechos e a equação, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, usando as equações de equilíbrio e definindo o diagrama de corpo livre, teremos
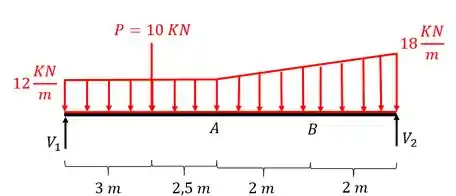
- Trecho AB
- X=5,5
- X=5,5
E assim terminamos o nosso segundo passo
Passo 4
Já sabemos a equação do nosso carregamento, definimos ele no nosso passo 2, mas para integração precisamos tomar muito cuidado, porque precisamos trocar o sinal do nosso carregamento, dessa forma, teremos que
Não se esqueça que sempre definimos a nossa carga com o sinal contrário para podermos fazer a integração.
Com isso já podemos ira pra o passo de determinação das equações, fazendo para cada trecho teremos,
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso ponto A, logo o nosso cortante nesse ponto é o somatório dos cortantes no ponto A, que será definido como positivo todos os vetores que estiverem para cima, e negativo todos os vetores que estiverem para baixo, dessa forma, cortando a nossa barra teremos
Substituindo na nossa equação teremos
Com isso a nossa equação do cortante será
Para calcular o momento fletor teremos que usar a outra fórmula, com isso teremos
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso ponto A, logo o nosso momento fletor nesse ponto é o somatório dos momentos no ponto A, que será definido como positivo todos os momentos que tracionarem as fibras da parte de baixo, e negativo todos os vetores que estiverem tracionando as fibras da parte de cima,
Substituindo na nossa equação teremos
Com isso a nossa equação do momento fletor será
Com isso atendemos os pedidos do nosso enunciado, descobrindo as equações do trecho AB assim como as extremidades desse trecho. Agora é só ficar tranquilo pra poder integrar os trechos que forem necessários e treinar mais um pouco, beleza, vamos aos exercícios então.
Resposta
Equações trecho AB
Cortante
Momento fletor