A figura abaixo mostra dois carros A e B conectados por três molas lineares com rigidez igual a , e . Não há atrito no sistema.
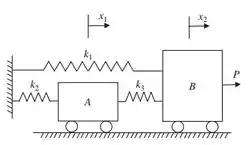
As molas estão em sua posição sem deformação quando a força aplicada é zero. A partir do seguinte problema de otimização para a função da energia potencial :
- Plote a superfície e as curvas de nível da função;
- Obtenha os deslocamentos otimizados e usando com ponto inicial e .
Passo 1
O enunciado nos dá uma função e pede para que encontremos o mínimo dela usando dois métodos.
A primeira coisa que devemos entender bem antes de atacar o exercício é qual é o problema de otimização. Para isto, devemos ter bem claro:
- “O que eu quero minimizar?”, definindo a função objetivo;
- “O que eu quero minimizar depende do quê?”, definindo as variáveis de projeto.
O que queremos minimizar é a energia potencial do sistema composto por dois carros conectados por molas, representada pela função dada no enunciado:
Logo, a energia potencial do sistema é minha função objetivo.
A função objetivo depende das variáveis e e de algumas constantes, como a rigidez das molas e a força , dadas pelo enunciado:
As variáveis e são as variáveis de projeto. Em outras palavras, queremos encontrar quanto e devem ser para que a energia potencial seja a menor possível.
Usaremos dois métodos para encontrar a posição dos carros A e B, representada por e , respectivamente, que minimizam :
- Gerando a superfície e a curvas de nível: usaremos as funções e para gerar os gráficos. Essas funções foram utilizadas no exercício anterior, mas vamos revê-las detalhadamente, para fixar bem como elas funcionam;
- Usando , com um chute inicial .
Passo 2
Vamos começar pela letra a. Em um novo script, entre as constantes listadas no passo 1:

Em seguida, vamos criar dois vetores, e , representando uma faixa de valores que e podem assumir:
![]()
Os vetores e vão de a , com um passo de . Eles servirão para criar os eixos X e Y dos gráficos da superfície e das curvas de nível pedidos na letra a.
Para podermos usar as funções e do MATLAB, devemos criar matrizes a partir dos vetores e , que contêm as coordenadas dos vetores. Faremos isso usando a função :
![]()
A função pega os vetores e , que têm elementos, e cria duas matrizes quadradas e , de tamanho . Cada linha da matriz é o vetor , repetido vezes. Já cada coluna da matriz é o vetor , repetido vezes.
Para ver bem direitinho como o funciona, você pode rodar o script que você escreveu até agora e pedir ao MATLAB para imprimir e e compará-los, e fazer a mesma coisa para e .
A função serve para auxiliar na criação de gráficos em três dimensões. A matriz será o eixo X do gráfico da superfície e das curvas de nível da função . Já a matriz será o eixo Y.
O eixo Z dos gráficos será a energia potencial. Por isso temos que criar uma matriz de tamanho com os resultados de para cada elemento das matrizes e . Digite no MATLAB a equação da energia potencial dada pelo enunciado, substituindo e pelas matrizes e :
![]()
Repare que usei o ponto ao lado das matrizes (por exemplo, ), para indicar que queremos realizar a operação em cada elemento da matriz.
Passo 3
Após ter criado as matrizes , e , podemos gerar os gráficos pedidos na letra a. Vamos começar com a superfície da função , que será gerada usando a função do MATLAB. A função tem o seguinte formato:
A plota uma superfície tridimensional com as curvas de nível abaixo dela. Ela gera um gráfico 3D com os valores da matriz no eixo X, da matriz no eixo Y e da matriz no eixo Z.
Vai dar para entender melhor aplicando a no exercício. Para gerar a superfície da função , adicione no script as seguintes linhas de código:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico da superfície em uma janela diferente do gráfico das curvas de nível.
Na segunda linha, o comando cria a superfície da energia potencial, tendo no eixo X, no eixo Y e no eixo Z.
Na terceira linha, o comando faz com que o gráfico tenha uma barra de cores indicando a intensidade da energia potencial.
Na quarta linha, dizemos que o eixo X do gráfico corresponde à variável de projeto , com o comando .
Na quinta linha, dizemos que o eixo Y do gráfico corresponde à variável de projeto , com o comando .
Finalmente, na sexta linha, indicamos que o eixo Z do gráfico corresponde à energia potencial, com o comando .
Vamos executar o programa pra ver essa superfície:

Repare que logo abaixo da superfície, no plano , temos as curvas de nível da superfície.
Para analisar a superfície e identificar o ponto de mínimo, na janela do gráfico, use o botão “Rotate 3D”, destacado abaixo, para “girar” a superfície.

Podemos ver as coordenadas dos pontos da superfície clicando neles. O ponto com menor que encontrei tem coordenadas , e . Contudo, eu não tenho certeza se esse realmente é o ponto de mínimo, pois é difícil encontrar o ponto exato de mínimo olhando só a superfície.
Vamos gerar as curvas de nível em um gráfico separado para ver se facilita.
Passo 4
Para gerar um gráfico de curvas de nível, usaremos a função , que tem a seguinte estrutura:
Esse comando cria um gráfico de curvas de nível, onde as isolinhas (linhas que ligam pontos de mesmo valor) correspondem aos valores da matriz . As matrizes e definem o eixo X e o eixo Y do gráfico de curvas de nível.
Para criar o gráfico de curvas de nível, digite no seu script os comandos:

Na primeira linha, pedimos ao MATLAB para criar uma segunda figura com o comando , para que o gráfico de curvas de nível seja gerado em uma janela diferente da janela onde foi plotada a superfície, no passo 3.
Na segunda linha, o comando cria o gráfico das curvas de nível da energia potencial, tendo no eixo X, no eixo Y e dando os valores para as isolinhas. As strings no final do comando () pedem ao MATLAB para mostrar o valor de cada curva do gráfico.
Na terceira linha, indicamos que o eixo X do gráfico do gráfico corresponde à variável de projeto , com o comando .
Na quarta linha, dizemos que o eixo Y do gráfico corresponde à variável de projeto , com o comando .
Bora rodar o programa pra ver as curvas de nível:
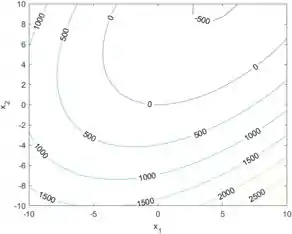
Note que é o mesmo desenho que temos no plano no gráfico da superfície, do passo 3.
Repare que as curvas com menor estão no canto superior direito do gráfico. Quanto mais afastado do canto superior direito, maior a intensidade de .
A curva de menor intensidade mostrada no gráfico é Isto significa que as coordenadas e que dão o mínimo estão no interior dessa curva e que a energia potencial mínima é pelo menos , mas pode assumir valores menores ainda.
Podemos ver as coordenadas de certos pontos ao clicar sobre o ponto no gráfico. No gráfico acima, o ponto com menor que encontrei tem coordenadas e , que dão um .
Passo 5
Encontrei dois pontos diferentes em cada gráfico, pois é muito difícil detectar o mínimo de uma função olhando somente as figuras. A análise dos gráficos serve apenas para termos uma noção de onde se localiza o ponto de mínimo. Na minha busca, com certeza deixei passar algum ponto com energia potencial menor.
Por isso, vamos usar o para encontrar o ponto de mínimo de maneira mais precisa (e responder à letra b do exercício).
Antes de implementar o , vamos relembrar como ele é:
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
Vamos criar uma nova função no MATLAB para representar a função objetivo . Abra um script novo e digite:

Chamei a função que contém a função objetivo de , mas você pode chamar do que quiser. tem como entrada o vetor , que tem dois elementos contendo as variáveis de projeto do problema de otimização: e . A saída de é a variável , que é a energia potencial que queremos minimizar.
Repare que tive que entrar novamente com as constantes da função , listadas no passo 1.
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:

Na primeira linha, entramos com o “chute” inicial das variáveis de projeto e , armazenado no vetor . O enunciado pediu para adotarmos .
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo, isto é, o menor valor possível de , partindo de .
A saída de é o vetor , de dois elementos, com os valores de que dão o menor possível.
A terceira linha calcula o valor de usando a função , tendo como entrada o vetor dado por . Desta forma, encontramos a energia potencial mínima.
Vamos executar o programa e ver qual o ponto de mínimo que o nos dá:

Encontramos que a energia potencial mínima é e ela ocorre em e . Até que não tá tão longe do ponto que encontrei na superfície, né?
Resposta
A energia potencial mínima é e ela ocorre em e .