Numa determinada localidade, a distribuição de renda (em reais) é uma v.a. X com f.d.p.
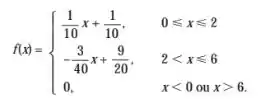
Escolhida uma pessoa ao acaso, qual a probabilidade de sua renda ser superior a $3.000,00?
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para dizer qual a probabilidade da renda ser alta. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser pensar que, por se tratar de um intervalo de valores, vamos precisar usar a integral.
Passo 3
Pronto!! Agora é só calcularmos a essa integralzinha!!