Um produtor de gelatina em pó está testando um novo lançamento e quer verificar em que
condições de preparo o produto seria mais bem aceito. Vinte e quatro donas-de-casa atribuíram notas ( a ) para o prato que produziram com o produto. Junto com o produto foram fornecidos quatro tipos de receitas: duas para doces ( e ) e duas para salgados ( e ). Feita a análise estatística, quais recomendações você faria ao produtor?
Discuta a validade das suposições feitas para resolver o problema.
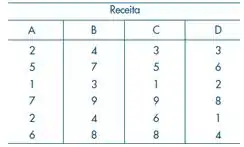
Passo 1
Para resolver este exercício, precisamos construir uma Tabela para a ANOVA:

Para o primeiro grupo (), temos:
Para o segundo grupo (), temos:
Para o terceiro grupo (), temos:
Para o quarto grupo (), temos:
Assim,
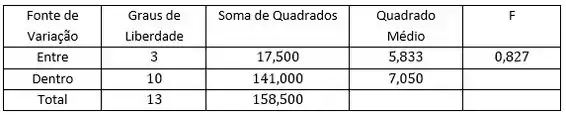
Considerando O valor crítico do teste é
Como , não rejeitamos a hipótese de que as médias são as mesmas para os grupos.
Resposta
Concluímos que as notas médias são iguais para os tipos de pratos.