Definindo funções recursivas
Produzido por Gustavo BarbosaTeoria
Introdução
Fala aí, aqui é o Guga do Responde Aí! Tudo bem com você?
Nesse tópico, nós iremos transformar os dois algoritmos que nós vimos no tópico anterior para o estudo de algoritmos recursivos em funções recursivas na linguagem C.
Parece coisa de outro mundo, né?

Mas calma, você vai ver que não é impossível. Então, vamos nessa!
Função recursiva de soma
A primeira função que transferiremos do teórico para a linguagem C é a função soma. Ela tem como objetivo realizar a soma de todos os elementos de um vetor de 5 posições.
A primeira coisa que nós devemos fazer é definir a função, para isso devemos chamá-la de soma e reconhecer que o seu tipo de retorno é int, já que o seu resultado será a soma de 5 números inteiros. Além disso, deve ter como parâmetros o índice atual do vetor e um ponteiro para ele.
Não se preocupe com a parte dos ponteiros, nós falaremos sobre eles futuramente. Enquanto isso, apenas considere que é uma forma de transferir todas as informações sobre o vetor (que foi criado no escopo principal) para o escopo local da função.
A imagem a seguir ilustra como a definição da função deve ser realizada:

Com a função soma definida, podemos criar o seu caso básico. Isso é, em que momento das chamadas recursivas o problema atinge sua forma trivial.
Muito simples! Como o vetor só possui 5 posições, quando a instância de posição 5 for passada como parâmetro para função, a mesma deve retornar um valor 0 (para não interferir na soma) e efetivamente realizá-la a partir de uma soma trivial.
Dá uma olhadinha na imagem abaixo, ela nos mostra como o caso básico é encaixado em uma função recursiva:
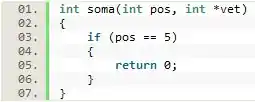
Certo, mas como as instâncias são criadas? E mais, como a soma é realizada na volta da recursão?
Vamos analisar o código abaixo:
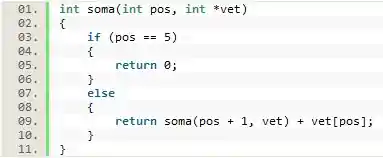
Basicamente, a função irá chamar a si mesma avançando uma posição pelos parâmetros, enquanto a variável pos não for igual a 5. No entanto, quando pos atinge o valor 5 é que a mágica realmente acontece.
Pois, o valor 0 será retornado e somado com o elemento na posição 4 do vetor, o resultado dessa operação, por sua vez, será retornado e somado com o valor do elemento da posição 3 e assim consecutivamente até que o resultado da soma dos 5 elementos seja retornado ao programa principal, para somente assim ser processado.
Eu sei que a coisa é meio maluca, mas uma dica de parceiro é imaginarmos todas as instâncias sendo criadas até que uma solução trivial é encontrada e da mesma forma imaginar como todas essas instâncias são retornadas na ordem de criação, gerando assim operações mais simples.
Função recursiva para o cálculo do fatorial
Beleza! Estamos pegando o jeito.

Assim como antes, a primeira coisa que devemos fazer é definir a função que será responsável por realizar o cálculo do fatorial de um número.
Essa função se chamará fat e terá seu retorno do tipo int, pois o resultado de sua operação é o fatorial de um número inteiro. Além disso, essa função deve ter apenas um parâmetro que é o número que terá o seu fatorial calculado.
A imagem a seguir ilustra como a função descrita pode ser definida:

Vamos agora para o caso básico, esse que só é encontrado quando n for igual a 0. Pois, por se tratar do fatorial de 0, temos como premissa que esse valor é 1, sendo ele o retorno da condição.
Para ficar mais fácil, podemos observar a imagem a seguir:
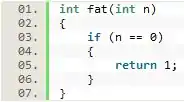
Ufa! Agora as coisas estão ficando mais direitas.
Mas então, você se lembra das regras dos algoritmos recursivos? Uma delas dizia que a cada criação de instância o caso básico deve estar mais próximo.
Para que isso aconteça, a função invocará a si mesma com parâmetros iguais a n – 1. Pois, quando o caso básico for verdadeiro, o valor 1 será retornado e multiplicado por 1 na instância anterior, o resultado dessa multiplicação, por sua vez, será multiplicado por 2 ao retornar novamente nas instâncias e assim sucessivamente até que o resultado de todas as multiplicações anteriores a n sejam, finalmente, multiplicadas por n.
Dessa forma, teremos o fatorial do número inicial, que será retornado ao escopo principal para ser processado.
No fim de tudo, a função fat deve ter a seguinte cara:

Muito massa, né?
Agora que nós já sabemos como definir funções recursivas, está na hora de resolvermos alguns exercícios de fixação.
Eu como sempre te esperarei na página aqui do lado.
