Funções Matemáticas
Produzido por Gustavo BarbosaTeoria
Fala aí, e bem vindo ao RespondeAí, está com dúvidas em Cálculo na faculdade? Aqui nós temos todo o conteúdo que você precisa para mandar bem nas suas provas. Com um conteúdo pensado especialmente para você feito pela nossa Equipe de Experts.
Vamos falar nessa página sobre funções que é um conceito que tem que ser muito bem compreendido porque estará presente em todos os assuntos da matéria de Cálculo. As funções sempre vão aparecer na sua prova, e o que vai mudar de semestre em semestre é o que você vai aplicar nelas, ou o método que você vai usar para resolvê-la, ou o gráfico que você vai ter que desenhar dela, e por ai vai...
Funções
Para falar de funções, vamos começar com uma pequena situação de exemplo: Imagine que você vai na sua lanchonete preferida e vai comer mini hambúrgueres.
Se cada mini hambúrguer custar
Para cada quantidade de hambúrgueres que você come, existe um preço correspondente. Se chamarmos a quantidade de hambúrgueres de
Se comêssemos um hambúrguer, pagaríamos 5 reais:
Se comêssemos dois hambúrgueres, pagaríamos 10 reais:
Repare que se comêssemos um número
Esta relação geral entre a quantidade e o preço , nesse caso, é o que chamamos de função. O preço depende de quantos hambúrgueres serão comprados, por isso falamos que o preço é uma variável dependente.
Os professores gostam de definir funções utilizando conjuntos, conforme esse esquema:
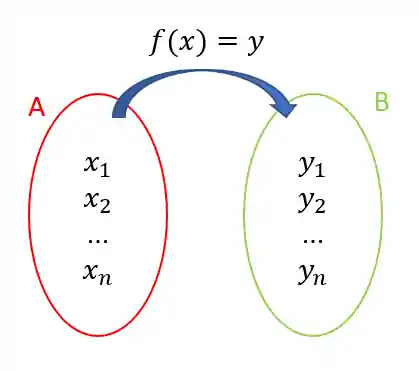
Onde um valor de
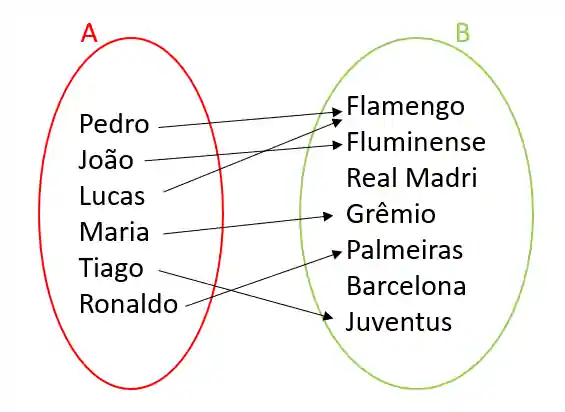
Então um mesmo time pode ter mais de um torcedor favorito, e para função ser bem definida todos devem ter um time favorito, e todos devem ter apenas
Nós representamos funções da seguinte maneira:
E conseguimos representar os pontos dessa função em um gráfico, por exemplo:
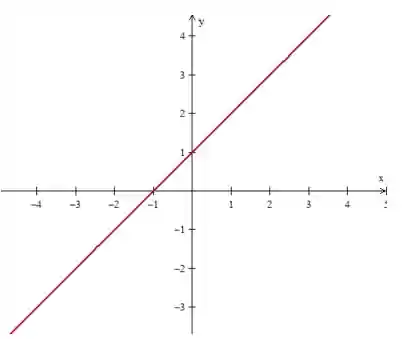
Ou então:
Ainda temos muito o que falar sobre funções, e tem tudo no nosso site, mas por enquanto vamos resolver um exercício de função enquanto entendemos o que é Domínio e o que é a Imagem de uma função, com nossa resolução Passo a Passo aqui em baixo:
Exercício
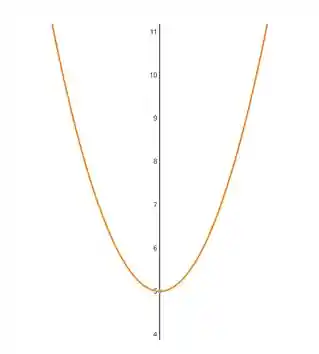
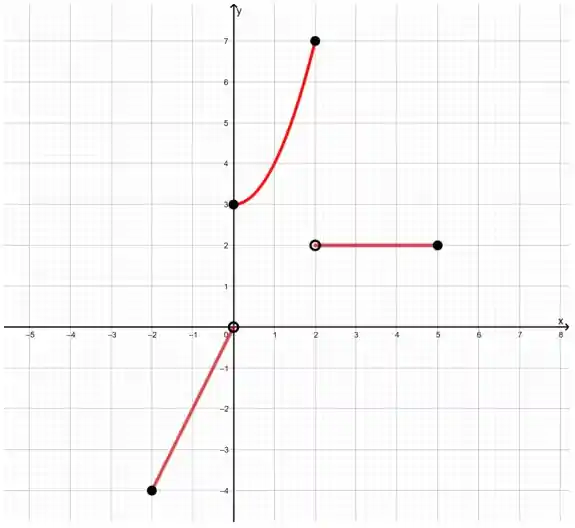
Observe o gráfico abaixo e determino os conjuntos domínio e imagem.
Passo 1
Vamos lá! Vamos considerar que o gráfico está gradeado de 1 em 1 já que está muito difícil de enxergar os valores. Então no primeiro Passo vamos focar em determinar o domínio dessa função, que serão todos os possíveis valores para
Olhando o gráfico podemos perceber que a função está definida para os valores de
Logo:
Passo 2
Ok, agora nós vamos procurar a imagem dessa função, a imagem são todos os valores as quais o
Para
Para
Para
Passo 3
Escrevendo tudo isso de uma forma mais elegante:
Resposta
Shoow, conseguiu pegar o que é Domínio e o que é imagem? Relaxa que ainda temos uma série de exercícios resolvidos para você no nosso site, aproveita e confere mais um de nossos exercícios um pouco mais avançado, mas solucionado em vídeo do tópico de funções:
Exercício
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Descreva o que é uma função e qual é a sua utilidade na linguagem C.
Passo 1
Uma função é um escopo, um lugar único (módulo) que você pode escrever instruções e reutilizá-las em outros trechos de código através de sua invocação no programa principal.
Passo 2
A grande utilidade de uma função é a economia de tempo de desenvolvimento, onde um algoritmo pode ser executado diversas vezes em um programa com diferentes valores sem a necessidade de reescrever tais instruções.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria.
Explique o motivo pelo qual variáveis passadas como parâmetro para uma função não têm os seus valores alterados mesmo que tais instruções de alteração estejam presentes na função.
Passo 1
Isso acontece, pois quando uma variável é passada como parâmetro para uma função, essa função cria uma cópia de seu valor em outro espaço de memória. A verdade é que dentro de uma função estamos trabalhando com as chamadas variáveis de cópia.
Resposta
Ou seja, apenas os valores são passados como parâmetro e qualquer alteração feita dentro da função modifica apenas a variável de cópia e não a original.
Mas lembre-se! Essa regra não é verdadeira quando nos referimos aos ponteiros.
Exercício Resolvido #3
Elaboração própria.
Crie uma função que recebe dois números inteiros como parâmetros e retorne a multiplicação deles.
Passo 1
A primeira coisa que nós vamos é definir o escopo da função.

Como os números recebidos serão inteiros e a multiplicação de dois inteiros origina um valor também inteiro, o tipo de retorno dessa função deve ser int. Além disso, devemos dar um nome a essa função, nesse caso o nome que daremos a ela é . Por fim, entre parênteses e separados por vírgula, devemos colocar os parâmetros esperados, que como mencionado anteriormente são dois números inteiros, por isso utilizamos e ambos do tipo int.
Passo 2
Com o escopo da função definido, podemos declarar a variável que receberá a multiplicação.

Passo 3
Por fim, basta atribuirmos o resultado da multiplicação dos valores recebido em e a e retornarmos o resultado.
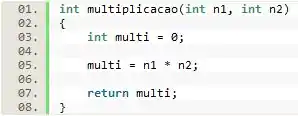
O resultado retornado será enviado ao escopo que invocou a função, que por sua vez, poderá realizar novos processamentos com ele.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Pontifícia Universidade Católica de Goiás – PUC de Goiás, Técnicas de Programação – Funções, Max Gontijo de Oliveira, pp. 02 – Exercício 14.
Fazer uma função que receba um caractere como parâmetro e retorne 1 caso o caractere seja uma consoante, ou 0 caso contrário.
Passo 1
A primeira coisa que nós temos que fazer é criar o escopo da nossa função.
Para isso, devemos primeiro falar para o programa o tipo de retorno dessa função, que por assumir apenas 0 ou 1 é int. Além disso, devemos na declaração decidir o nome dessa função, nesse caso . Por fim e entre parênteses devemos falar os parâmetros que essa função deve receber, nesse caso um único caractere .
Passo 2
Com o escopo da função definido, podemos elaborar o código que ela executará quando chamada.
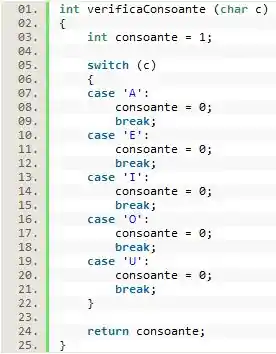
Onde basicamente declaramos uma variável do tipo int e a inicializamos com o valor 1 (supondo que o caractere passado por parâmetro é uma consoante). Após isso, utilizamos a estrutura switch para pegar o caractere armazenado por e compará-lo com todas as vogais através de casos, caso um deles seja verdadeiro receberá 0.
No término da função o valor de será retornado da seguinte forma: se o caractere armazenado por for uma consoante o valor de retorno (armazenado por ) será 1, caso contrário o valor será 0.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Pontifícia Universidade Católica Do Rio Grande do Sul – PUC do Rio Grande do Sul, Funções e Procedimentos, Sílvia Moraes e Egídio Terra, Adaptação do exercício 10.
Faça uma função que recebe um valor inteiro e verifica se o valor é par ou ímpar.
Passo 1
Começaremos o nosso programa com o escopo da função que iremos declarar.
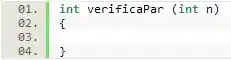
A lógica dessa definição está baseada em usar o retorno do valor 1 para indicar que o número é par e o valor 0 ímpar, dessa forma podemos dizer ao programa que o tipo do retorno da função é int. Como se trata de uma função que faz a verificação da paridade de um número, nada melhor do que chamá-la de . Por fim, basta dizermos ao programa quais serão os parâmetros dessa função, nesse caso um número inteiro.
Passo 2
Com o escopo da função definido, basta escrevermos o código que ela executará.
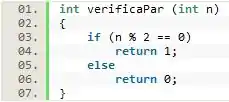
Aqui nós não temos segredo, simplesmente utilizamos o comando condicional for para verificar se o resto da divisão de por 2 é igual a 0. Caso a condição seja verdadeira, temos que retornar o número 1 para indicar que se trata de um número par, caso contrário o retorno deve ser 0.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Pontifícia Universidade Católica Do Rio Grande do Sul – PUC do Rio Grande do Sul, Funções e Procedimentos, Sílvia Moraes e Egídio Terra, Adaptação do exercício 06.
Faça uma função que recebe a idade de uma pessoa em dias, meses e anos e retorna essa idade expressa apenas em dias.
Passo 1
Vamos iniciar a declaração dessa função com a definição do seu escopo.

Como o resultado desse procedimento consiste em retornar a vida total de algo em dias, o tipo do seu retorno deve ser int. Além disso, o nome que podemos dar a essa função é . Por fim, basta fornecermos as informações dos parâmetros ao programa, nesse caso serão 3 números inteiros: para dias, para meses e para anos.
Passo 2
Com o escopo da função definido, nós podemos desenvolver o código que ela executará.
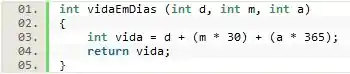
A lógica é bastante simples, basicamente declaramos uma variável que é inicializada com a soma entre os dias recebidos como parâmetros, os meses multiplicados por 30 e os anos multiplicados por 365.
Ao final, basta retornamos o dado armazenado em , já que o mesmo se trata da soma de todas as representações (meses e anos) já convertidas em dias.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Pontifícia Universidade Católica Do Rio Grande do Sul – PUC do Rio Grande do Sul, Funções e Procedimentos, Sílvia Moraes e Egídio Terra, Exercício 18.
Faça uma função que receba um valor inteiro e positivo e calcula o seu fatorial.
Passo 1
Como de costume, para criarmos essa função devemos começar pelo seu escopo.
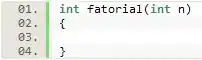
Por ser uma função que calcula o fatorial de um número, o tipo de seu retorno é int. Além disso, nada melhor do que chamarmos ela de , pois é o cálculo que ela realiza. Por fim, basta dizermos para o programa os parâmetros que ela espera para funcionar, nesse caso é um único número inteiro.
Passo 2
Com o escopo definido, podemos codificar normalmente os comandos utilizados para o cálculo do fatorial de um número.

A lógica desse código consiste em utilizar uma estrutura de repetição, nesse caso for, para a realização de multiplicações sucessivas com até que o mesmo seja o fatorial de e seja retornado ao término da execução do laço.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Elaboração própria.
Faça uma função que receba um caractere minúsculo como parâmetro e retorne esse mesmo caractere em maiúsculo (não é necessário verificar a entrada).
Passo 1
Vamos começar a declaração da nossa função pelo seu escopo.
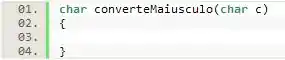
Como essa função irá retornar um caractere, o seu tipo ideal de retorno é char. Além disso, por se tratar de uma função de conversão, podemos chamá-la de . Por fim, basta informarmos ao programa os parâmetros que essa função espera, nesse caso um caractere .
Passo 2
Como o enunciado nos diz que não é necessário verificar a entrada, podemos ter certeza de que só serão passados como parâmetro dessa função caracteres minúsculos.
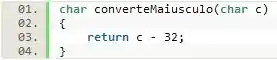
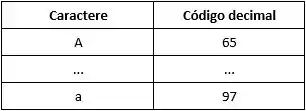
Sendo assim, tudo o que devemos fazer é utilizarmos os nossos conhecimentos da tabela ASCII para realizar essa conversão. Isso pois, todos os caracteres na linguagem C podem ser tratados como números inteiros e como a letras maiúsculas são localizadas antes das minúsculas, basta realizarmos a subtração dessa diferença de localização (que é 32).
Resposta
Ei, a resposta está no passo a passo :)