Introdução às matrizes
Produzido por Gustavo BarbosaTeoria
Introdução
Fala aí, aqui é o Guga do Responde Aí! Tudo bem com você?
Anteriormente nós batemos um papo sobre o que são e como funcionam os vetores. Sem perder o fio da meada dessas estruturas, hoje nós iremos conversar um pouco sobre matrizes.
Então, vamos nessa!
Matriz
De maneira geral, uma matriz nada mais é do que um vetor com mais de uma dimensão. De fato, essas duas estruturas possuem uma forte relação, o que faz com que na programação uma matriz unidimensional seja um vetor e um vetor com mais de uma dimensão seja uma matriz.

Pegou a referência? Agora que você já conhece essa relação, para facilitar o nosso entendimento iremos adotar algumas referências de menção.
Quando quisermos nos referir a uma estrutura unidimensional utilizaremos a nomenclatura “Vetor” (estrutura que nós visualizamos através de uma linha de dados computacionais nos tópicos anteriores). No entanto, quando formos nos referir a estruturas com mais de uma dimensão, chamaremos as mesmas de “Matriz”.
Beleza! Agora vamos parar com esse papo chato de nomenclatura e vamos ver de fato o que é uma matriz, utilizando como exemplo uma de 2 dimensões (matriz bidimensional):
Nessa matriz, ao invés de organizarmos os dados em apenas uma linha (como acontece nos vetores), temos a adição de colunas. Dessa forma, um dado é identificado através do cruzamento entre uma linha e uma coluna.
Vamos para um exemplo!
Se observarmos bem, ao relembrar um jogo conhecido como Campo Minado veremos que o propriamente dito campo se trata de uma matriz e as minas espalhadas pelo mesmo estão localizadas em coordenadas dela.
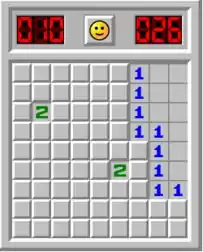
Sendo assim, começando pelo tamanho, vamos recriar alguns dos conceitos desse jogo em uma matriz computacional. Dá uma olhadinha na seguinte matriz:
O tamanho de uma matriz é dado pela quantidade linhas e colunas que a mesma possui. Então, se uma matriz possui m linhas e n colunas dizemos que ela possui é da ordem m x n.
Dessa forma, considerando que as coordenadas que armazenam o número 1 se trata de locais com a presença de mina e as coordenadas que armazenam o número 0 aquelas que estão livres, nós acabamos de criar um campo minado em formato de matriz computacional de ordem 3 x 3.
Mas o que de fato é a coordenada de uma matriz?
É bem simples, coordenadas são o cruzamento entre linhas e colunas de uma matriz. Sendo assim, utilizando o mesmo exemplo do campo minado reduzido que criamos, podemos referenciar as posições perigosas (aquelas que possuem minas) através de coordenadas.
Portanto, a coordenada é tão perigosa quanto a coordenada , pois ambas armazenam o número 1 (contém mina). Onde o primeiro número da coordenada referência uma linha e o segundo uma coluna da estrutura. Vale lembrar que assim como nos vetores, as matrizes possuem suas contagens iniciadas no número 0.
Criando uma matriz
Criar uma matriz é muito semelhante a criar um vetor, a única diferença se encontra na adição da declaração do número de colunas que a mesma terá. Dessa forma, para criar o campo minado reduzido utilizado nos exemplos, basta codificarmos as seguintes linhas:
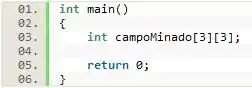
E acabamos de criar uma matriz denominada campoMinado de ordem 3 x 3 e tipo int. Em uma forma geral, podemos resumir a criação de uma matriz através do seguinte código:

Molezinha, né? Agora que já tivemos a nossa introdução às matrizes, está na hora de resolvermos alguns exercícios de fixação para aprendermos de verdade o conceito.

O portal já vai fechar! Te encontro na página aqui do ladinho.
Criando uma matriz
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Explique o que é uma matriz e qual é a sua diferença em relação a um vetor.
Passo 1
Uma matriz é uma estrutura de ordem capaz de armazenar um conjunto de dados computacionais.
Passo 2
Diferentemente do vetor, uma matriz é uma estrutura com mais de uma dimensão. Isso significa que para acessar os dados armazenados nela, sempre será necessário cruzar índices.
Para ficar mais fácil, observe a seguinte matriz:
Para acessarmos as posições em que o valor 1 está armazenado, devemos realizar o cruzamento de uma linha com uma coluna (matriz bidimensional). Logo, as posições que possuem o valor 1 armazenado são:
- Linha 0 e Coluna 0;
- Linha 1 e Coluna 1;
- Linha 2 e Coluna 2.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria.
Um dos jogos mais famosos do mundo, conhecido no Brasil como “Jogo da Velha” é representado a seguir com uma partida:

Em um determinado dia o seu professor de programação passou como trabalho a criação do jogo da velha no computador. Tendo estudado o conteúdo do trabalho no Responde Aí, você teve a brilhante ideia de representar o campo do jogo em uma matriz.
Tendo como base a partida acima, como ficaria a sua representação em uma matriz na linguagem C sendo que as seguintes regras foram passadas por seu professor:
- O número 0 deve representar que a casa está vazia;
- O número 1 deve representar o jogador com bolinha;
- O número 2 deve representar o jogador com xis.
Passo 1
Para entendermos com essa partida de jogo da velha ficará em uma matriz computacional, basta realizarmos a substituição de xis, bolinha ou casa vazia pelos seus respectivos números (passados como regra por seu professor).
Resposta
Ao término da substituição, a matriz representará a partida apresentada no enunciado a partir de dados computacionais:
Exercício Resolvido #3
Elaboração própria.
A imagem a seguir representa um dos campos de um jogo muito conhecido como Batalha Naval:
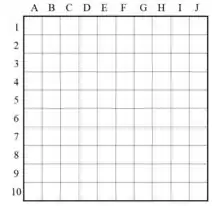
Recrie esse campo na linguagem C utilizando para isso uma matriz.
Passo 1
Antes de efetivamente criarmos essa matriz em um programa, devemos analisar a sua ordem. Como se trata de um campo com 10 linhas e 10 colunas, podemos dizer que a matriz será bidimensional e terá ordem 10.
Passo 2
Com a ordem identificada, basta realizarmos a sua declaração no programa:
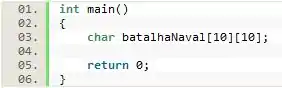
A primeira coisa que nós devemos fazer é avisar para o programa o tipo que essa matriz terá, mas como o enunciado não diz como os navios serão identificados, iremos supor que será utilizado o primeiro caractere do nome do navio. Logo, a matriz será do tipo char.
Em seguida, devemos definir um nome para a matriz, nesse caso a denominados de . Por fim, entre colchetes diferentes, informamos ao programa a quantidade de linhas e colunas e finalizamos o comando com ponto e vírgula.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria.
Crie uma matriz do tipo int chamada de ordem .
Passo 1
A criação dessa matriz é feita da seguinte forma:
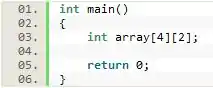
Onde a primeira coisa que nós fazemos é informar ao programa o tipo que a matriz terá, nesse caso int. Em seguida e separada por um espaço em branco informamos o nome da matriz, que é . Por fim, basta informamos a ordem entre colchetes diferentes, onde o primeiro valor entre colchetes representa as linhas e o segundo valor, também entre colchetes, representa as colunas dessa matriz.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria.
Indique quais são os índices que compõem a diagonal principal de uma matriz de ordem .
Passo 1
Os índices que formam a diagonal principal de são:
- (0, 0);
- (1, 1);
- (2, 2);
- (3, 3);
- (4, 4);
- (5,5);
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Elaboração própria.
Suponha que a seguinte matriz represente uma partida de dama:
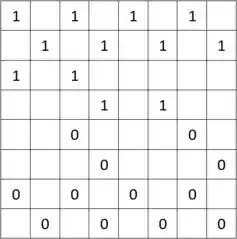
Onde:
- O número 0 representa as peças brancas;
- O número 1 representa as peças pretas.
Indique nessa matriz o índice de peças que correm o perigo de serem “comidas” no próximo turno.
Passo 1
Se o turno for do jogador preto, a seguinte peça corre perigo:
- (4, 2).
- (3, 3);
- (3, 5).
Passo 2
Por outro lado, se o turno for do jogador branco, as seguintes peças correm perigo:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Elaboração própria.
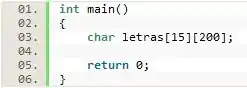
Crie uma matriz de caracteres com 15 linhas e 200 colunas chamada .
Passo 1
A primeira coisa que devemos fazer é declarar ao programa o tipo da matriz, nesse caso char. Após isso, devemos falar ao programa o nome dessa matriz, que é seguido da quantidade de linhas e colunas entre diferentes colchetes (15 e 200, respectivamente).
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Elaboração própria.
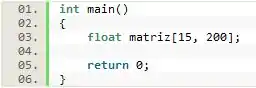
Observe a seguinte declaração de :
Qual é o motivo pelo qual o programa apresenta erro de compilação?
Passo 1
O programa não compila, pois, a declaração de está errada, mais precisamente na parte dos índices (linhas e colunas). Isso acontece, pois as linhas e as colunas devem ser declaradas em colchetes diferentes e não em apenas um separadas por vírgula.
Passo 2
O trecho de código correto para a declaração de é:
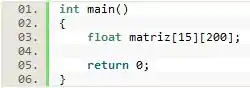
Dessa forma, acabamos de declarar uma matriz denominada do tipo ponto flutuante (float) com 15 linhas e 200 colunas.
Resposta
Ei, a resposta está no passo a passo :)