Operadores da linguagem
Teoria
Introdução
Fala aí, aqui é o Guga do Responde Aí! Tudo bem com você?
Nos tópicos anteriores nós fomos introduzidos aos operadores da linguagem C, nesse tópico nós iremos conversar de forma mais aprofundada sobre esse mesmo assunto.
Beleza, para começar, como são utilizados os operadores na linguagem C? Os operandos são sempre números?
Nós iremos descobrir as respostas dessas e outras perguntas ao decorrer desse tópico, então vamos nessa!
Operadores aritméticos
Que os operadores aritméticos são utilizados para realizar operações matemáticas básicas nós já sabemos, mas como eles são escritos dentro de um código?
Para responder essa pergunta, nada melhor do que um exemplo! No exemplo abaixo nós escolheremos o operador de soma, mas fique ciente que a utilização apresentada é análoga para todos os outros operadores aritméticos binários.
Exemplo: suponha que você tenha que declarar uma variável inteira que seja inicializada com o valor , além da variável inteira você deve declarar outra variável , do tipo ponto flutuante, que será inicializada, após o processamento de , com o valor da primeira variável mais .
A primeira coisa que nós iremos fazer é declarar e inicializar a variável inteira, que nesse exemplo terá a denominação e a variável que será inicializada posteriormente, nesse exemplo denominada como :
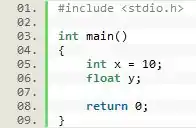
Agora, temos que inicializar a variável de tipo ponto flutuante, mas antes observe a seguinte análise:
Nós sabemos o valor inicial com que foi declarado, porém nós não podemos simplesmente inicializar com o valor igual a . Isso acontece, pois a variável sofrerá alterações antes do programa efetivamente utilizar .
Logo, o valor com que será inicializado é igual ao valor de naquele estágio do programa mais :
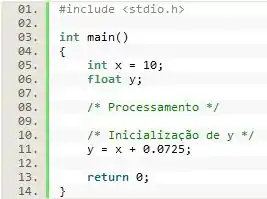
Você viu como o operador de soma foi útil nesse caso? Agora ficou fácil, pois podemos elaborar a forma geral de utilização dos operadores aritméticos:
Onde:
- resultado é a variável que irá armazenar o resultado da operação;
- operando1 e operando2 podem ser variáveis, constantes que estão definidas (#define), constantes que não estão definidas (números utilizados diretamente como é o caso do ) e até mesmo expressões aritméticas (veremos em tópicos posteriores).
Mas onde se encaixam os operadores aritméticos unários?
Eles são utilizados para incrementar ou decrementar o valor do dado armazenado por uma variável em uma unidade.
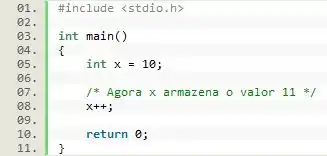
Vale lembrar que tudo aquilo que pode ser feito com um operador unário, também pode ser realizado através de um operador binário:
Operadores relacionais
Os operadores relacionais são utilizados para realizar comparações entre variáveis, constantes que estão definidas e constantes que não estão definidas. Basicamente, um operador relacional se trata de um comparador capaz de verificar se a relação por ele estabelecida é verdadeira ou falsa.
Como o retorno de uma comparação relacional é booleano, ou seja, só pode assumir valores, nos casos em que a relação é verdadeira o retorno é o valor , já nos casos em que a relação é falsa, o retorno é o valor .
Exemplo:
Observe o programa a seguir:
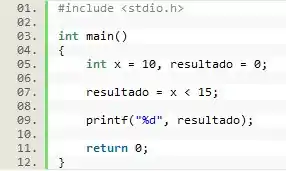
Qual será o resultado da impressão realizada na linha 08 do programa?
O valor impresso será , pois é igual a e é menor que . Logo, o valor atribuído a na linha 07 do programa é uma vez que a relação é verdadeira, sendo esse o valor que será impresso na linha de código posterior.
Vale lembrar que a utilização é análoga para os outros operadores relacionais e que se caso a relação fosse falsa, como é o caso da comparação maior que entre os operandos e (), o valor de atribuição e posteriormente impressão seria .
Lembrete: como feito no exemplo acima, não é comum utilizar o valor do retorno de uma comparação relacional. Isso acontece, pois na grande maioria dos casos, as comparações utilizando operadores relacionais são parâmetros de estruturas condicionais ou de estruturas que necessitam de condições de parada, essas que veremos futuramente.
Com isso, podemos elaborar a forma geral de utilização dos operadores relacionais em sua forma mais comum:
Onde:
- operando1 e operando2 podem ser variáveis, constantes que estão definidas, constantes que não estão definidas e até mesmo expressões relacionais (veremos em tópicos posteriores).
Operadores lógicos
Os operadores lógicos são responsáveis por unir duas ou mais comparações relacionais e, de acordo com uma tabela verdade, gerar um resultado booleano.
Isso ainda está meio complicado, né? Então, dá uma olhada no exemplo a seguir.
Exemplo: suponha que em uma de suas disciplinas existam dois elementos avaliativos, um trabalho que aborda o conteúdo de todo o semestre e uma prova final. Caso a sua nota no trabalho seja maior ou igual a e a nota da sua prova final seja maior ou igual a , você será aprovado na disciplina. Querendo antecipar a sua aprovação, você decidiu desenvolver um programa que verifica se você passou ou não na disciplina.
Para que o programa possa verificar se você passou, ele deve utilizar um operador lógico && em que os operandos serão duas comparações relacionais ( e ):
Por que isso dá certo? Pois a tabela verdade do operador lógico E (&&) é:
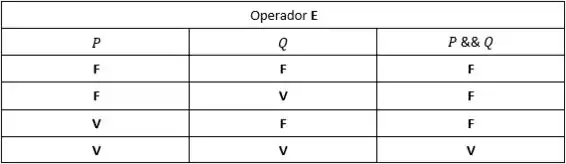
Onde:
- é o resultado do primeiro operando (comparação relacional);
- é o resultado do segundo operando (comparação relacional);
- é o resultado da comparação lógica como um todo.
Sendo assim, você só passará na matéria quando e forem verdadeiros, em outras palavras, quando a nota da prova final for maior ou igual a e a nota do trabalho for maior ou igual a .
Lembrete: verdadeiro é análogo a , já falso é análogo a . O computador só trabalha com números, porém visualizar como verdadeiro e falso é mais fácil para nós humanos (tipo booleano).
Ficou bem mais simples, não acha? Agora, nós só precisaremos lembrar das tabelas verdade dos operadores lógicos e fazer as assimilações com os resultados das comparações relacionais presentes como operandos!
Abaixo estão as tabelas verdade dos outros dois principais operadores lógicos.
Tabela verdade do operador lógico OU (||):
Mas até aqui todos os operadores lógicos eram binários, existe algum operador lógico unário?
A resposta é SIM!
Tabela verdade do operador lógico NÃO (!):
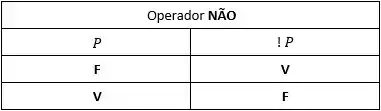
Por se tratar de um operador lógico unário, a sua tabela verdade acaba ficando reduzida uma vez que só existe um operando.
Agora que você já sabe quem são os operadores da linguagem C e como utilizá-los, está na hora de resolvermos alguns exercícios de fixação, você não acha?
Sem preguiça, Jedi! Te encontro ali na outra página.
Operadores relacionais
Operadores lógicos
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Em relação aos operadores lógicos, complete a seguinte tabela verdade:
Passo 1
O operador lógico NÃO é muito simples, nós não precisamos atribuir significado ao operando , pois independente do valor que ele assuma, o valor de ! será o oposto.
Como assim?
Se for falso, como é o caso representado pela primeira linha de valores booleanos da tabela verdade, então ! é verdadeiro.
Passo 2
Se for verdadeiro, como é o caso representado na segunda linha de valores booleanos da tabela verdade, então ! é falso.
É só isso! Nós acabamos de completar a tabela verdade do operador lógico NÃO, simples né?
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria.
Em relação aos operadores lógicos, complete a seguinte tabela verdade:
Passo 1
Para completarmos essa tabela verdade de maneira simples, precisamos atribuir significados tanto para quanto para . Dessa forma, imagine que representa a capa de proteção de um jogo e o C.D em que esse jogo está armazenado.
Agora, suponha que você está em uma loja de jogos prestes a comprar o maior lançamento do ano.
A primeira situação que pode acontecer é você pedir o lançamento e ele não estar mais disponível na loja, isso significa que tanto quanto são falsos.
Nessa situação, nós conseguimos comprar o jogo? Ou melhor, nós temos a capa E o C.D do jogo?
A resposta é não! Por esse motivo a condição é falsa.
Passo 2
A segunda linha de valores booleanos representa a situação em que a loja possui o lançamento, porém apesar do C.D estar funcionando perfeitamente a capa do jogo está danificada.
Você como um grande colecionador, aceitará uma capa danificada E o C.D do jogo?
A resposta é não! Por esse motivo a condição novamente é falsa.
Passo 3
A terceira linha de valores booleanos representa a situação em que a loja possui o lançamento, porém apesar da capa protetora estar em boas condições o C.D está riscado.
Como você quer jogar o game no primeiro dia de lançamento, aceitará uma capa em boas condições E um C.D riscado?
A resposta é novamente não! Por esse motivo a condição é falsa.
Passo 4
A última linha de valores booleanos representa a situação em que a loja possui o lançamento em perfeito estado, ou seja, a capa protetora e o C.D estão intactos.
Por fim, você aceitará uma capa protetora E um C.D em perfeitas condições?
Claro que sim! Por esse motivo a condição é verdadeira.
Nós acabamos de terminar a tabela verdade do operador lógico E, a exclusividade dessa tabela é que && só será verdadeiro se tanto quanto forem verdadeiros.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria.
Em relação aos operadores lógicos, complete a seguinte tabela verdade:
Passo 1
Preencher uma tabela verdade é muito simples, nós só temos que arranjar alguns significados para ela, imagine que representa um carro e representa uma moto.
Analisando a primeira linha de valores booleanos da tabela verdade, observamos que tanto quanto são falsos, isso significa que no nosso exemplo não temos um carro e não temos uma moto.
Para verificar || , devemos nos perguntar se temos um carro OU uma moto?
A resposta é não! Por isso essa condição é falsa.
Passo 2
Analisando a segunda linha de valores booleanos da tabela verdade, observamos que e , isso significa que no nosso exemplo não temos um carro, mas temos uma moto.
Para verificar || , devemos nos perguntar se temos um carro OU uma moto?
A resposta é sim! Dessa forma, a condição verdadeira.
Passo 3
Analisando a terceira linha de valores booleanos da tabela verdade, observamos exatamente o inverso do passo anterior, isso significa que no nosso exemplo temos um carro, mas não temos uma moto.
Portanto, assim como antes, nós temos um carro OU uma moto?
A resposta é sim! Por isso essa condição também é verdadeira.
Passo 4
Analisando a última linha de valores booleanos da tabela verdade, observamos que tanto quanto são verdadeiros, isso significa que no nosso exemplo temos um carro e temos uma moto.
Mais uma vez, nós temos um carro OU uma moto?
A resposta é sim! Por esse motivo nós temos mais uma condição verdadeira.
Nós acabamos de concluir a tabela verdade do operador lógico OU! Viu como adicionar exemplos torna as coisas extremamente mais fáceis?
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria.
Escreva um código na linguagem C que imprima na tela o valor do dado gerado no resto da divisão entre os números 13 e 7.
Passo 1
A primeira coisa que devemos fazer é definir o escopo do nosso programa.
Como uma impressão deve ser realizada, temos que incluir as funções de entrada e saída presentes na biblioteca padrão stdio.h.
Além disso, devemos declarar a função main() que será responsável por alocar e executar o código principal do nosso programa.
Passo 2
Com o escopo do programa definido, devemos declarar a variável que irá armazenar o dado gerado na operação descrita no enunciado.
Como o resto da divisão entre os números 13 e 7 irá gerar um número inteiro, a variável que irá armazená-lo deve ser de mesmo tipo.
Com essas informações em mente, nós temos que realizar a declaração da variável mencionada (linha 05).
Passo 3
Com a variável declarada, podemos realizar a atribuição do dado que ela irá armazenar.
Como devemos armazenar como dado o resto da divisão entre dois números, devemos utilizar o operador % (operador aritmético de resto da divisão ou módulo). Onde o primeiro operando é o número 13 e o segundo operando o número 7.
Com a operação formada, basta realizarmos a atribuição do valor gerado por ela a variável que nós declaramos no passo anterior (linha 07).
Passo 4
Por fim, nós só temos que realizar a impressão do dado gerado na operação, para isso utilizaremos a função printf().
Como a variável x é a responsável por armazenar esse dado, ela será impressa (linha 08) seguida de uma quebra de linha.
Vale lembrar que nesse programa de exemplo nós utilizamos a variável x, mas ela poderia assumir qualquer nome que faça sentido com o dado que ela armazena, como por exemplo restoDivisao.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria.
Observe o seguinte código:
O que será impresso na tela quando o programa executar o comando presente na linha 10 do código apresentado?
Passo 1
A primeira coisa que devemos fazer para responder o que será impresso na tela, é identificar o que está sendo atribuído a variável X. Para isso, precisamos nos lembrar da tabela verdade do operador lógico E:
Passo 2
Como a atribuição feita representa a situação em que o primeiro operando é verdadeiro e o segundo é falso, nós temos que analisar a tabela verdade na linha em que e :
Com a tabela reduzida é fácil identificar que o valor booleano que está sendo atribuído a X é falso, porém como na linguagem C os valores booleanos são representados através de números inteiros, temos que , sendo esse o valor que é impresso na tela.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Elaboração própria.
Dada a condição:
||
Onde:
- é igual ao valor 3;
- é igual ao valor 1.
Defina o seu valor de retorno.
Passo 1
Analisando a condição, nós conseguimos observar que ela é formada por dois operandos, esses que expressam comparações relacionais, interligados pelo operador lógico OU.
Sendo assim, a primeira coisa que devemos é subdividir essa condição para analisarmos de forma individual cada operando.
Sendo o primeiro:
O enunciado nos disse que a variável possui valor igual a 1, por esse motivo podemos reescrever essa comparação relacional da seguinte forma:
1 é igual ao valor 2?
A resposta é não! Sendo falso o resultado da comparação expressa pelo primeiro operando da condição dada.
Passo 2
O próximo passo para definir o valor de retorno da condição, é analisar o valor de retorno do seu segundo operando:
Assim como o passo anterior, o enunciado nos forneceu o valor da variável , reescrevendo a comparação relacional, ela ficará da seguinte forma:
3 é menor que o valor 4?
A resposta é sim! Então, temos como verdadeiro o valor de retorno do segundo operando.
Passo 3
Com o valor de retorno dos dois operandos da condição previamente conhecidos, basta analisarmos a tabela verdade do operador lógico OU assimilando o primeiro operando a e o segundo operando a .
A tabela verdade do operador lógico OU é essa aqui:
Destacando a linha em que e , que é o valor de retorno das comparações relacionais que analisamos nos passo anteriores, teremos a seguinte tabela:
Como a tabela verdade expressa todos os possíveis resultados de um operador lógico dada uma condição específica e a condição que nós destacamos na tabela acima é exatamente aquela que compõem a condição dada pelo enunciado, podemos afirmar que o valor de retorno dela será verdadeiro, ou melhor, o valor inteiro 1 já que estamos falando da linguagem C.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Elaboração própria.
Dada a condição:
- &&
Qual será o seu valor de retorno quando ?
Passo 1
Analisando a condição geral, nós conseguimos observar dois operandos, que representam comparações relacionais, unidos por um operador lógico E.
Sendo assim, a primeira coisa que devemos fazer é analisar o primeiro operando e definir o valor de retorno de sua comparação relacional.
25 é menor ou igual a 25?
A resposta é sim! Logo, se trata de uma comparação relacional verdadeira.
Passo 2
Conhecendo o valor de retorno do primeiro operando, nós podemos realizar a análise do segundo operando da condição geral, que é:
)
Nós sabemos que o enunciado afirmou que . Substituindo esse valor na comparação, nós ficamos com:
1 é menor que 5?
A resposta é novamente sim! Dessa forma, o retorno da comparação expressa pelo operando 2 também é verdadeira.
Passo 3
A última coisa que devemos fazer é definir o valor de retorno da comparação lógica definida pelo operador E, para isso basta analisarmos a sua tabela verdade:
Onde:
- ;
- .
Como analisado nos passos anteriores, nós sabemos que as duas comparações relacionais são verdadeiras. Com isso, para descobrirmos o valor de retorno da condição geral, que é dada pela união de duas comparações através do operador lógico E, basta assimilarmos o valor fornecido pela tabela verdade desse operador quando .
Como podemos ver na imagem em que apenas a linha que queremos é destacada, o retorno da comparação lógica quando e é verdadeiro, ou melhor, o valor inteiro 1.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Elaboração própria.
Dado o seguinte trecho de código:
O que será impresso na tela quando o programa finalizar a execução do comando presente na linha 08?
Passo 1
Para sabermos o que será impresso na tela, devemos saber o que a variável x está armazenando naquele momento de execução do programa.
Começaremos essa análise identificando o tipo do dado.
Sabemos que o valor que está sendo atribuído a x na linha 07 se trata do resultado gerado a partir de uma operação NÃO. Por se tratar de uma operação lógica, também sabemos que o resultado será booleano.
Passo 2
Para encontrarmos esse valor booleano, devemos analisar a tabela verdade do operador lógico NÃO especificamente na condição em que , pois o único operando presente nessa operação é o número 54 e para a linguagem C qualquer valor maior que 0 é considerado verdadeiro.
Analisando a tabela verdade destacada exatamente na condição em que , conseguimos observar com facilidade que o valor de retorno da operação é falso.
Resposta
Com base nas análises o valor impresso na tela é 0, pois a linguagem C representa retornos booleanos a partir de números inteiros, onde 0 representa falso e 1 verdadeiro.