Recursividade
Produzido por Gustavo BarbosaTeoria
Fala ae! Aqui é o Samuel do Responde Aí, e hoje a gente vai aprender sobre funções recursivas, uma ferramenta poderosa que vai nos ajudar bastante em diversos problemas!
Pra entender o que são essas funções, nada melhor do que começarmos com um exemplo, então bora lá!
Função recursiva
Vamos analisar a função e ver o que acontece quando a chamamos no nosso código:

Começamos na linha 5 indicando pro C++ que teremos uma função chamada no código. Depois, nas linhas 7 a 11 temos o nosso código principal, a única coisa que ele faz é chamar a função, que ainda precisa ser criada.
Então, a função é definida nas linhas 14 a 18, primeiro ela imprime uma mensagem, mas repara como na última linha essa função é chamada novamente dentro da sua própria rotina. Dessa forma, quando a chamamos dentro da , ela inicia a sua rotina printando “Ola mundo!” e depois se chama novamente, então printa “Ola mundo!” e se chama novamente... esse processo continua e seria infinito, mas o próprio computador faz com que o programa seja encerrado com o retorno de .
Uma função como essa, que chama ela mesma dentro de sua rotina, é chamada de função recursiva.
Uso de uma função recursiva
Vamos analisar a seguinte sequência:
Eai, pegou a referência?

Essa é a sequência de Fibonacci, muito famosa por aparecer na natureza em diversas formas, desde o formato da concha de caramujo até as presas de um elefante. Nela, cada novo termo da sequência é a soma dos dois termos anteriores, então sua fórmula de recursão é dada por , onde é o n-ésimo termo da função e
Imagine que você precisa do valor correspondente ao . Tentar calcular ele na mão seria algo muito trabalhoso! Logo, que tal montarmos um programa que nos ajude nisso?
Vamos tentar montar um algoritmo para calcular um termo genérico dessa sequência. Para isso, vamos declarar a função , que receberá um inteiro não negativo , e retornará o n-ésimo termo, que será o .
Quando vamos trabalhar com recursividade, o primeiro passo seria definir os valores iniciais. Nesse caso, vamos definir que . Isso já será o suficiente para começarmos.

Perceba que, dessa forma, quando for enviado 0 ou 1 para a função, ele retornará o valor 1, que seria equivalente aos valores iniciais da sequência.
Agora vamos implementar a recursividade. O termo será a soma da própria função aplicada aos dois termos anteriores, e :
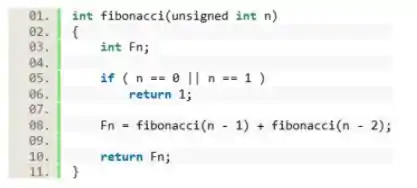
Agora podemos verificar como o nosso código está funcionando e calcular o :

Aqui, quando definimos na linha 09, o programa faz o cálculo usando a função que definimos anteriormente, pra isso, ele precisa dos valores de para e , que nesse ponto valem e , então a função é chamada novamente, o que faz gerar novos valores de e . Esse processo vai se repetindo até que a função chegue nos valores de e que definimos no início.
Todo esse processo é feito nos “bastidores” do C++ e como saída, temos apenas o valor que pedimos: !
Loop infinito
No primeiro caso mostrado da função , temos um exemplo de uma péssima forma de se utilizar o método recursivo, pois acabamos caindo num loop infinito, no qual o programa vai ficar rodando aquela função indefinidamente.
Para a recursão, esse tipo de caso não é favorável, portanto, devemos evitá-lo. Mas como fazer isso?
Bom, a solução varia de caso pra caso. Possíveis soluções seriam reestruturar o algoritmo de recursão para que não caia num loop infinito ou impor uma quantidade limite de vezes que a função pode ser chamada.
Vamos pegar a seguinte sequência como exemplo:
Essa sequência é uma Progressão Aritmética (P.A ), cujo termo inicial é e a razão é .
Uma possível relação recursiva para uma PA é ou ainda . Vamos montar a função recursiva para essa PA. Para isso, vamos definir os dois primeiros termos como e . De forma semelhante a função de , teremos:

No entanto, caso colocássemos essa função para rodar do jeito que está, teríamos um problema! Vamos colocar , por exemplo. A função irá chamar as funções e . Ao ser chamada, a função irá chamar a função , que chamará a função novamente, que chamará a função ...

Isso irá continuar indefinidamente, ou seja, caímos num loop infinito.
Uma maneira de contornarmos isso, seria reescrever a relação de recursividade de tal forma que ela dependa apenas de valores anteriores:
Poderíamos ainda reescrever dessa forma:
Com isso, temos o seguinte algoritmo:

E agora sim!

Dessa forma, não temos mais aquele problema do loop infinito!
Agora que já entendemos como funcionam as funções recursivas, como usá-las e, principalmente, como não usá-las, vamos partir para alguns exercícios de fixação.
Uso de uma função recursiva
Loop infinito
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Crie uma função em C++ que recebe um número inteiro e retorna, de forma recursiva, o valor de (fatorial de ).
Passo 1
Eai, tudo beleza?
Vamos começar lembrando o que é recursão! A recursividade é um mecanismo que permite uma função chamar a si mesma. E isso vai ser bem conveniente no caso do fatorial, você já já vai ver porquê.
Nessa questão, vamos iniciar declarando uma função chamada . E os parâmetros dessa função vão ser as variáveis e
Como ambos e são valores inteiros, podemos declarar tanto os parâmetros, quanto o retorno da função como .
![]()
Passo 2
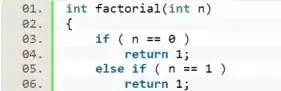
Agora, vamos definir os casos iniciais da nossa recursão, que são os casos em que a função não chama a si mesma. No caso da função fatorial, sabemos que:
- 0! = 1
- 1! = 1
Isso será o suficiente para estabelecermos o caso inicial para a nossa função.
Passo 3
Vamos estabelecer a relação de recursão. Vamos analisar o para isso.
Perceba que , então podemos escrever como
O , por sua vez, pode ser escrito como
O pode ser escrito como , e assim segue.
Dessa forma, temos
Percebeu como a gente tem um fatorial dentro de outro fatorial dentro de outro fatorial...?
É por isso que a recursão é interessante aqui, pois vamos chamar a função dentro dela mesma!
Implementando isso no nosso código, temos:

A função vai chamar a si mesma, até que N seja igual a 0 ou 1.
Resposta

Exercício Resolvido #2
USP – Introdução a Ciência da Computação II – Lista de Exercícios 2: Recursividade – adaptada
Desenvolva, de forma recursiva, uma função que recebe um inteiro e retorna que é dado por:
Passo 1
Eae, tranquilo?
Vamos analisar a função proposta chamando-a de . Essa função recebe um argumento inteiro e retorna um valor também inteiro, logo, podemos declarar e o seu argumento como .
![]()
Passo 2
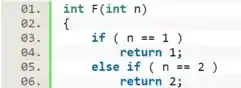
Agora, vamos colocar as condições iniciais.
Pelo enunciado nós temos os valores de para e , então vamos colocar um condicional usando um pra quando assumir esses valores, a função retornar os valores que queremos:
Passo 3
Por fim, temos que adicionar a recorrência para os casos diferentes de e .
Nesse caso, vamos usar a equação dada:
![]()
Resposta

Exercício Resolvido #3
UFU – Computação - Programação Procedimental - Aula Prática: Funções Recursivas
A função de Ackermann é definida para valores inteiros e não negativos e da seguinte forma:
- , se
- , se e
- , se e
Faça uma função recursiva para implementá-la. Qual o valor de A(3,2)?
Passo 1
Eae, tudo tranquilo?
Para a função proposta nesse enunciado, teremos como parâmetros dois valores, e , ambos inteiros não negativos, assim como o valor a ser retornado pela função, então, podemos declarar esses valores como .
![]()
Passo 2
Vamos colocar os casos iniciais para a função de Ackermann. Temos o caso em que , no qual será retornado , e em que e , no qual será retornado
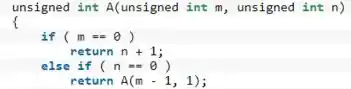
Repare que não é necessário especificar que no segundo caso, pois foi definido como , logo, temos e o caso de já foi considerado no primeiro condicional, ou seja, se a função não terminou no primeiro condicional, significa que é necessariamente maior que 0.
Passo 3
Agora, vamos acrescentar a recursividade dada por:
, se e
Similar ao caso anterior, não há necessidade de especificar as condições de e , pois são as únicas condições que sobraram para serem analisadas.
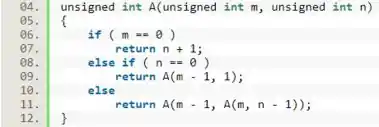
Perceba que é possível passar a própria função como um parâmetro, pois o retorno de foi declarado como do mesmo tipo dos parâmetros de .
Passo 4
Por fim, basta calcularmos o valor de . Para isso, vamos incluir a biblioteca e imprimir na tela tal valor.
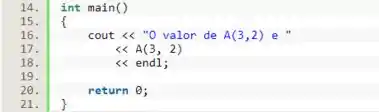
Resposta
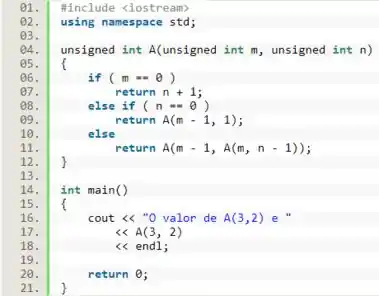
Para o valor de A(3,2), temos:
![]()
Exercício Resolvido #4
UFU – Computação - Programação Procedimental - Aula Prática: Funções Recursivas - adaptada
Escreva uma função recursiva que calcule o número de grupos distintos com pessoas que podem ser formados a partir de um conjunto de pessoas. A definição abaixo da função define as regras:
- , se
- , se
- , se
Caso sejam passados valores de e que não estejam especificados nas condições acima, faça a função retornar 0.
Passo 1
Eae, tudo tranquilo?
Nessa questão, estamos trabalhando com conceitos de combinatória e, por isso, devemos trabalhar com valores inteiros, pois a combinação de termos é melhor definida dessa forma. Nesse contexto, vamos declarar a função com os dois argumentos, e , e o retorno do tipo .
![]()
Passo 2
Agora, vamos colocar as condições iniciais que foram dadas. Caso , a função retorna e caso , ela retorna .

Passo 3
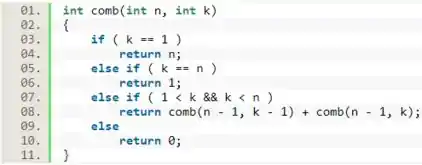
A seguir, vamos adicionar a relação de recorrência dessa função, que é dada por:
, se
![]()
Por fim, vamos acrescentar o caso de nenhuma das condições anteriores serem atendidas. Como foi definido no enunciado, caso isso aconteça, a função deve retornar .
![]()
Resposta
Exercício Resolvido #5
Universidade Federal de Uberlândia – Lista de Exercícios – Recursão
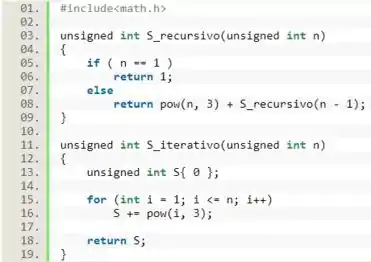
Escreva uma função recursiva que calcule a soma dos primeiros cubos:
Chame essa função de . Crie também uma função que calcule essa soma de forma iterativa (usando laços de repetição, como e ) e chame-a de .
Passo 1
Eae, tudo tranquilo?
Vamos iniciar essa questão focando na função . Pra isso vamos relembrar que a recursividade é um mecanismo que permite uma função chamar a si mesma.
Para começarmos a trabalhar com essa função, precisamos determinar a recursão que será utilizada e os casos iniciais.
Para encontrarmos a nossa relação de recursividade, vamos escrever a função em função de :
Essa é a nossa relação de recursividade. Ela vai funcionar tipo um loop. Como, ao chamar um , será chamado sempre um valor menor de até que , precisamos estabelecer nosso caso inicial, que é o caso que a função não vai chamar a si mesma (). Esse vai ser o .
Com base nisso, vamos declarar essa função com ambos, retorno e parâmetro, como , pois só serão utilizados valores positivos nessa função.
![]()
Passo 2
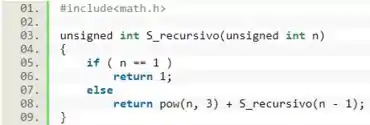
Já tendo definido o valor inicial para a nossa função de recursão, , vamos colocar isso no nosso código usando um condicional:

A seguir, vamos colocar a relação de recursão. E, para calcular o , vamos incluir a biblioteca e utilizar a função para calcular potências.
Passo 3
Agora, vamos focar na função . Como ele também irá trabalhar apenas com valores interos positivos, vamos declarar essa função e o seu parâmetro como .
![]()
A seguir, para calcularmos a soma dos cubos por meio de um laço de repetição, é necessário criar uma variável para acumular o valor dessa soma, que deverá ter valor inicial nulo. Vamos chamá-la de .
![]()
Vamos usar um laço de para que acumule o valor de cada cubo, e esse loop precisa fazer iterações. Então vamos definir a variável começando do e indo até o .
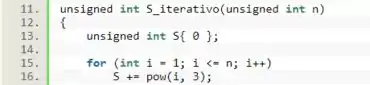
Por fim, basta retornarmos o valor de ao término do laço de .
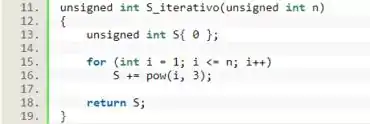
Resposta
Exercício Resolvido #6
UFU – Computação - Programação Procedimental - Aula Prática: Funções Recursivas
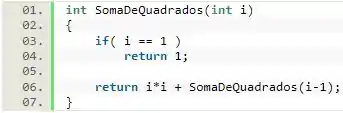
Seja a somatória abaixo. Faça uma função recursiva para realizar o cálculo.
Passo 1
Eai, tudo beleza?
Nessa questão, nós temos que calcular uma soma de termos de forma recursiva. Uma boa maneira de fazermos isso, é fazermos uma função que recebe um valor e chama ela mesma, mas enviando um valor . Para que a função pare a recursividade, podemos fazer com que ela retorne , caso o valor enviado para ela seja , já que esse é o menor termo do somatório que está no enunciado.
Para começar o nosso código, vamos declarar a nossa função :
![]()
Passo 2
Dentro dessa função, a primeira coisa que vamos fazer é colocar o condicional para verificar se é igual a . Nesse caso, nós retornamos , encerrando a função.
![]()
Passo 3
Caso a função não esteja encerrada, ou seja, não é , vamos retornar + . Dessa forma, ao final da recursão, essa função retornará o somatório que queremos.
![]()
Resposta
Exercício Resolvido #7
Universidade Federal de Uberlândia – Lista de Exercícios – Recursão
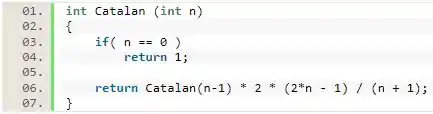
Os números de Catalan são definidos pela seguinte recursão
- , se
- , se
Alguns números desta sequência são:
Faça uma função recursiva que receba um número e retorne o N-ésimo número de Catalan.
Passo 1
Eai, tudo beleza?
Nessa questão, nós temos que calcular os números da sequência de Catalan usando recursividade. Nesse caso, vamos iniciar a nossa função checando se o valor passado como parâmetro é igual a . Caso seja, vamos retornar , assim como o enunciado nos mostra funciona a sequência de Catalan. Esse será o caso que vai determinar o fim da recursividade.

Passo 2
Agora, vamos implementar a recursividade da sequência. Para isso, vamos fazer o nosso programa retornar . Dessa forma, vamos enviar sempre um número menor para a nossa função até que ele seja igual a e a recursividade seja encerrada.
![]()
Resposta
Exercício Resolvido #8
Universidade Federal de Uberlândia – Lista de Exercícios – Recursão - adaptada
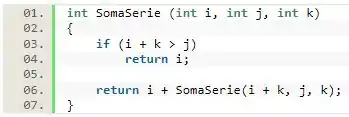
Escreva, usando a linguagem C++, uma função recursiva, que devolva a soma da série de valores do intervalo , com incremento .
Passo 1
Eai, tudo tranquilo contigo?
Nessa questão, nós temos que fazer uma função que soma uma série de valores que podem ir de até , variando de em . Para fazer isso, primeiramente vamos pensar no caso em que vamos encerrar a recursão. Essa recursão deve ser encerrada no caso de ser maior do que o final do intervalo, ou seja . Nesse caso, vamos retornar o somente o valor de :

Passo 2
A seguir, vamos implementar a nossa recursividade. Nela, vamos retornar o valor de somado ao valor de . Desse modo, a função vai retornar o menor valor do intervalo somado à função recebendo o valor do novo intervalo com o incremento, que vai retornar o menor valor desse intervalo + a função iniciando no intervalo ... e esse processo vai continuar até que o valor passado no inicia do intervalo somado ao incremento seja maior que .
![]()
Resposta