Teoria
O que são algoritmos
Mano, não sei se você lembra, mas um programa de computador é, basicamente, um conjunto de instruções que a gente passa pro seu computador executar. Esses conjuntos de instruções têm um nome: algoritmos! Mas algoritmos não são apenas para computadores. Todo conjunto de instruções é chamado de algoritmo, e a gente usa pra TUDO!

Por isso que hoje a gente vai bater um papo sobre o que são algoritmos e sua importância na programação.

Vou te mostrar: imagine a gente ensinando uma criança chamada Enzo a atravessar a rua. É uma tarefa que parece óbvia e a gente faz automaticamente, mas pra explicar pra uma criança, a gente tem que falar um passo a passo...

Mais ou menos assim:
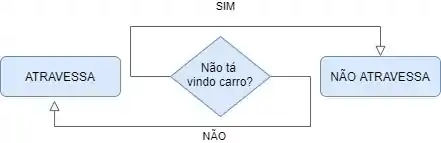
“Enzo, primeiro você tem que olhar pros dois lados da rua. Você só deve atravessar caso não esteja vindo carro de nenhum dos dois lados. Caso esteja vindo, você não atravessa, ok?”

Viu?! Mesmo parecendo muito óbvio, a gente tem um passo a passo. Tudo que a gente precisa fazer na vida pode ser descrito com um passo a passo (algoritmo). Mas como aqui a gente tá interessado em ensinar pra um computador, e não pra uma criança, fica um pouquinho mais difícil. Lembra que os computadores não entendem nosso idioma? Então... A gente tem que organizar esse algoritmo de forma mais engessada. Tipo assim:

Bem robótico, sacou? A gente precisa começar a pensar igual robô!

Existem vários algoritmos...
Ok, a gente fez o algoritmo. Mas tu tem que se ligar que nossos programas precisam usar a melhor solução possível pra que nossos computadores não se “esforcem” demais a toa, entende?! Pra isso, a gente precisa fazer um código top!

Mas cara, tenta achar alguma diferença entre o algoritmo que a gente fez antes e esse aqui:

Reparou que, apesar da gente ter mudado a pergunta e as respostas, o resultado é exatamente o mesmo?! É exatamente isso que eu queria te mostrar. No entanto, nem sempre é assim. Olha:
Aqui a gente mudou algumas coisas de novo, mas o resultado dessa vez é que o Enzo vai morrer, cara!!!

Por isso, tenho que te avisar que, nas provas de programação discursivas (quando você tem que escrever o código), existem várias respostas certas. Afinal, a forma que você pensa não precisa ser igual a de todo mundo, né?! Mas o seu professor vai descontar ponto se a sua solução for desgastante demais pro computador, então talvez você precise pensar um pouquinho sobre a sua solução antes de entregar a prova, ok?!

Eficiência dos algoritmos
Beleza! Agora você já sabe que ideal é você sempre escrever a solução que seja mais fácil pro computador realizar, mas pra isso ficar ainda mais claro pra você, vou te dar um exemplo maneiro:
Imagina que você pegou um dicionário pra saber o significado da palavra “insofismável”. Cara, a primeira coisa que você tem que fazer é achar essa palavra no dicionário pra depois ler o significado, certo?! Mas um dicionário tem muuuitas palavras, se você for lendo de uma em uma até achar “insofismável”, tu vai sofrer pra achar!

Porém, você pode, malandramente, começar a procurar a partir das palavras que começam com “i”, certo? Você vai ter eliminado muito trabalho desnecessário se você começar a procurar dentre as palavras que começam com “i”.

O seu algoritmo de ler palavra por palavra, apesar de funcionar, é um algoritmo ineficiente, pois tinha trabalho desnecessário. Na hora de fazer algoritmos pra computador, você tem que pensar sobre se o algoritmo tá fazendo trabalho desnecessário pra não perder ponto, jae?!

Fluxogramas
Além disso, antigamente era muito comum utilizarem diagramas pra expressar algoritmos. Esses diagramas eram chamados de fluxogramas, e às vezes cai em provas alguns algoritmos expressados utilizando essa notação. Pra você entender como funciona essa notação, vou te mostrar um fluxograma de um algoritmo que te ajuda a decidir entre comprar uma bicicleta ou se casar, olha:
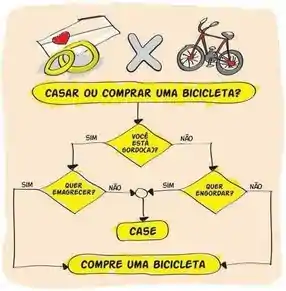
Com esse algoritmo, você consegue chegar na resposta que você espera seguindo um conjunto de instruções, viu?! Porém, nas suas provas não costuma cair coloridinho e bonitinho assim, mas os nossos exemplos anteriores foram todos expressos em fluxograma. Vou colocar de novo um aqui pra você dar uma olhada:

Existe toda uma teoria de como fazer fluxogramas, mas esse conteúdo não é mais cobrado atualmente. O máximo que pode acontecer é seu professor ser bem coroa e colocar um fluxograma desses na prova. O macete é você simplesmente seguir as setinhas que tu vai entender, jae?

A gente se vê no próximo episódio!
Existem vários algoritmos...
Eficiência dos algoritmos
Fluxogramas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
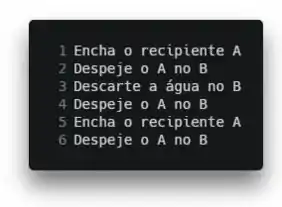
O Dexter, mascote do Responde Aí, precisa de exatamente 4L de água pra tomar banho. Mas ele só tem uma torneira e dois recipientes, A e B, com capacidades de 5L e 3L, respectivamente.
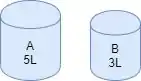
Escreva um algoritmo que consiga deixar exatamente 4L de água no recipiente A pra ajudar o Dexter.
Passo 1
E aí, seu doido! Nesse exercício a gente precisa utilizar a combinação dos dois recipientes pra conseguir os 4L de água que o Dexter precisa.

A primeira coisa que a gente tem que ter em mente é que não existe apenas uma solução. Exercícios de programação costumam ter várias respostas possíveis, mas a melhor solução é a que dá menos trabalho (menos etapas). Então, se você conseguiu de outra forma e com o mesmo número de etapas (ou menos), não tá errado, ok?!

Vamo lá! A gente pode começar enchendo o recipiente A.
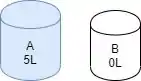
Passo 2
Aí a gente despeja tudo que der no recipiente B
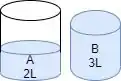
Se liga que agora a gente tem 2L no A e 3L no B.
Passo 3
O que a gente pode fazer é descartar tudo que tá no recipiente B. Agora, a gente sabe que só tem 2L de água no A.
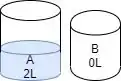
Passo 4
E a gente pode despejar os 2L que restam em A no B!
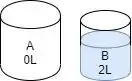
Agora, o B tem 2L, e falta 1L pra chegar ao seu limite. Enquanto isso, o A ficou vazio!
Passo 5
A gente pode encher de novo o recipiente A!
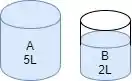
Passo 6
Agora, se liga só, a gente pode despejar o conteúdo de A até preencher o B (que faltava 1L). O resultado é que vamos ter 4L no recipiente A.
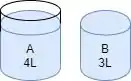
Aeee! Agora sim o Dexter pode tomar banho com a quantidade de água que ele gosta!

Te vejo no próximo exercício!
Resposta
Exercício Resolvido #2
Elaboração própria
Desenhe um fluxograma para o seguinte algoritmo:
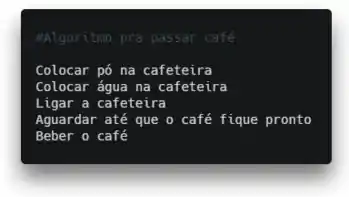
Passo 1
Fala aí, meu parceiro! Nessa questão, você precisa lembrar que fluxograma é aquele diagramazinho de balões que ligam as instruções do algoritmo, tá ligado?!

Esse tipo de diagramação serve pra que a gente possa olhar pro nosso algoritmo e seguir o seu fluxo mentalmente, de forma a encontrar possíveis bugs (bug = situação onde o algoritmo não funciona da forma que a gente espera).

A primeira coisa que a gente tem que fazer e ficar ligado nos formatos dos balões:
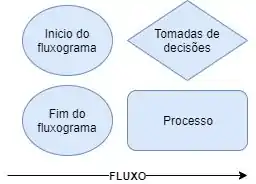
Obs: repare que o início de um fluxograma tem o mesmo símbolo do final. Vamos iniciar nosso fluxograma com um balão elíptico e nossa primeira ordem dentro, que é “colocar o pó na cafeteira”.

Eu escrevi só “colocar o pó” pra não ficar muito grande dentro do balãozinho. Mas não tem problema, ok?! O principal aqui é o fluxo do algoritmo.
Passo 2
Bom, depois de colocar o pó a gente faz o que?!

A gente coloca água na cafeteira. Como esse é um processo normal, que não começa e nem termina o fluxograma, a gente vai usar o retângulo (aqui o retângulo tá com as bordas arredondadas pra ficar mais bonitinho, mas é um retângulo, ok??!).
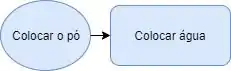
A setinha indica o fluxo do nosso algoritmo. Ou seja, a gente começa colocando a água e assim que a gente colocar a água, a gente coloca o pó!
Passo 3
O próximo passo é ligar a cafeteira. Essa instrução também é um processo normal, assim como colocar água. Sendo assim, a gente coloca dentro de um retângulo também!

As setinhas, mais uma vez, indicam o fluxo. Até aqui, esse fluxograma diz que a gente primeiro coloca o pó e vai seguindo as setinhas os próximos processos, em ordem.
Passo 4
A próxima instrução é um pouco mais difícil. Qual deve ser o símbolo desta instrução?! Bom na verdade, a gente tem que quebrar essa instrução em duas.

Relaxa que a gente vai conseguir! Vamos isolar só essa instrução pra gente falar melhor sobre ela:
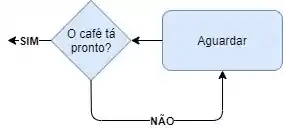
Olha, “aguardar” é um processo normal, certo?! A gente quer esperar o café ficar pronto, mas a gente não sabe quanto tempo vai demorar. Então, a gente pode aguardar um pouco e checar se o café já passou. Caso não esteja pronto ainda, aí a gente espera mais um pouco e repete o processo. Sacou?!
O símbolo losango (tomada de decisão) tem duas saídas, que dependem da resposta pra pergunta dentro dele. A gente vai seguir o fluxo (setinha) da resposta da pergunta. Então, até agora, nosso fluxograma tá assim:
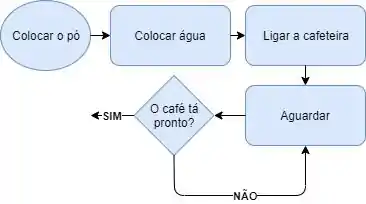
Obs: se liga também que o formato final pode ser o formato que você quiser! Eu podia ter continuado o fluxograma pro lado, também podia ter feito tudo na vertical, etc. O importante é manter a ordem na setinha, jae?!
Passo 5
Agora, pra finalizar, a gente só precisa do último processo, que é beber o nosso cafezinho gostosinho!

Como esse é o processo final do nosso algoritmo, a gente vai usar o símbolo de fim (que é o mesmo de início). Olha:
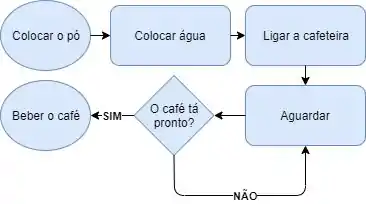
Olha que lindinho esse nosso fluxograma! Repara que na hora de escrever, os símbolos são importantes. Mas na hora de ler um fluxograma, o macete é não precisa ficar se preocupando com os símbolos, beleza?! Basta seguir as setinhas.

Valeuuu! Até a próxima!
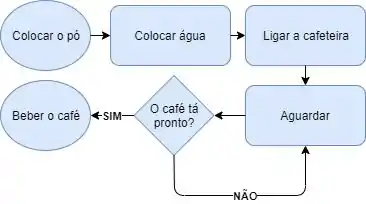
Resposta
Exercício Resolvido #3
Elaboração Própria
Selecione a alternativa incorreta sobre a natureza dos algoritmos.
- Algoritmos são passo-a-passos necessários pra resolver determinado problema
- A receita de bolo da sua avó é um algoritmo
- Um algoritmo tem que ter uma sequência finita de passos
- Algoritmos complexos são melhores
Passo 1
Fala aí, mano!! Chega aí pra gente resolver mais um exercício de algoritmos. Vamo lá!

Cara, quando é múltipla escolha, a gente pode ir analisando item por item. Então vem comigo, vamos olhar pra alternativa A. Vou colocar ela aqui pra você não ter que ficar subindo pra ler o enunciado!
- Algoritmos são passo-a-passos necessários pra resolver determinado problema
- A receita de bolo da sua avó é um algoritmo
- Um algoritmo tem que ter uma sequência finita de passos
- Algoritmos complexos são melhores
Cara, é sim. Esse é a própria definição de algoritmos, e eles estão presentes na nossa vida em tudo que fazemos. Quando entramos na faculdade e andamos até a nossa sala de aula, estamos executando vários algoritmos mentalmente, mesmo sem perceber.

A gente anda até chegar na curva, depois vira pra esquerda, depois sobe a escada, depois vira pra direita.... Pensa bem, você com certeza conseguiria escrever um manual de como chegar na sua sala de aula. Você consegue fazer seguindo um passo-a-passo, beleza??

Essa tá certa!! Mas cuidado, o enunciado pede a INCORRETA, mano! Não vacila! Vamos olhar pra b.
Passo 2
A receita da minha avó é um algoritmo??? Ih! O que minha vózinha tem a ver com isso???

Cara, na verdade, é. Lembra que a gente acabou de falar que é algoritmos são conjunto de instruções? (a gente falou agorinha mesmo, não tem nem um minuto hahaha). Então! Se nossa vózinha consegue seguir um conjunto de instruções (receita) e fazer aquele bolo maravilhoso, então sim! É um algoritmo!

Essa também tá certa, beleza?? Vamo pra próxima!
Passo 3
Vish, já pensou se sua avó fosse fazer um bolo e nunca conseguisse terminar? Se a receita fosse infinita ela nunca ia conseguir acabar o bolo! A coitada ia ficar batendo a massa pra sempre!!

E se algoritmos são instruções pra RESOLVER algum determinado problema, então sequências infinitas não são algoritmos. Pensa comigo, se for infinito, então você nunca vai resolver o problema. Se você não consegue resolver o problema, então não é algoritmo, entendeu?!

Doideira, né??? Mas é isso aí! hahaha. Essa aqui também tá certa!!
Passo 4
Rapaz, todas as outras estavam certas, então essa aqui com certeza tá errada. Acabou! Valeu!
Mentira, tô zoando. Volta aqui!

Cara, na verdade, os melhores algoritmos são justamente os que dão menos trabalho. Quanto menor o grau de complexidade de um algoritmo, melhor! Justamente o contrário do que a alternativa tá falando.

É bom você lembrar disso na hora das suas provinhas de prog, ok? Se o seu programa funcionar, mas for mais complexo do que o necessário, você pode perder ponto! Sempre tenta achar a solução mais simples, ok? SIMPLICIDADE = DELICIA
Essa aqui tá errada, brow! Marca essa! hahahah
VALEUUU!
Resposta
Alternativa D.
Exercício Resolvido #4
Elaboração Própria
Imagina que um fazendeiro precisa atravessar um rio de canoa, mas ele tem um lobo, uma ovelha e um repolho. O fazendeiro só pode levar uma coisa por vez na viagem, e pode fazer várias viagens. Se a raposa for deixada sozinha com a ovelha, ela comerá a ovelha. Se a ovelha for deixada sozinha com o repolho, ela comerá o repolho. Escreva um algoritmo pra ajudar o fazendeiro a atravessar o rio e chegar com todos os seus pertences.

Passo 1
Fala ai, maninho! Antes de tudo, queria te lembrar que exercícios de algoritmo não costumam ter somente uma solução, beleza? Então, vamo lá! Vou te mostrar uma delas.

Uma coisa importante a se notar antes da gente começar é que a gente tem 2 problemas: deixar o lobo com a ovelha e deixar a ovelha com o repolho. Mas se a gente deixar o lobo com o repolho não tem problema, né? Afinal, lobos não comem repolho! Hahah. Vamos usar esse fato pra desenvolver nosso algoritmo.

Em primeiro lugar, vamos levar a ovelha, já que deixar o lobo com o repolho não trás nenhum problema.

Passo 2
Agora, vamos voltar pra buscar mais alguma coisa, e deixar a ovelha do outro lado do rio mesmo.

Passo 3
Beleza! Agora a gente precisa levar mais alguma coisa. Vamos levar o repolho!

Repara que se a gente deixar o repolho com a ovelha, teremos problemas. Na verdade, se a gente tivesse trazido a raposa em vez do repolho, teríamos problemas também, certo?? Então, se liga na malandragem: vamos deixar o repolho e levar a ovelha de volta!

Passo 4
Se liga que se a gente deixar a ovelha com nada em nenhum dos lados. Como a gente pode resolver isso?! A gente pode deixar a ovelha no lugar da raposa e levar a raposa. Se liga só.

Olha! Se a gente deixar a raposa com o repolho, não vai ter problema! Muahahahah trolamos a raposa!
Passo 5
Agora a gente volta pra pegar a ovelha.


Pronto! Atravessamos tudo!!

Valeu, maninho! Espero que tenha entendido sobre o que são algoritmos e, talvez, se divertido durante o processo.
Até a próxima!
Resposta

Exercício Resolvido #5
Elaboração Própria.
A “Torre de Hanói” é um quebra-cabeça que a gente movimenta discos por hastes. A imagem abaixo mostra 3 hastes, A, B e C, com 4 discos iniciados na haste A.
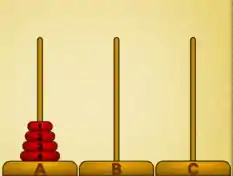
O objetivo é mover os 4 discos pra haste C.
Porém, existem algumas regras:
- Você só pode mover um disco por vez;
- Você não pode colocar um disco maior em cima de um menor.
Obs: lembre-se que o melhor algoritmo é aquele com menor custo, ou seja, menor quantidade de movimentos que você puder!
Passo 1
Cara, esse é um problema clássico no meio da computação. Você pode ver como um joguinho, que a gente pode resolver como um quebra cabeça. Um quebra cabeça difícil pacas!

Vamos a uma das possíveis resoluções. Mas antes, queria te lembrar que não tem só uma solução, beleza? Problemas de algoritmo podem ter vááárias possíveis soluções, você pode encontrar a sua. Mas sem esquecer que o ideal é usar o mínimo de movimentos possíveis, beleza?

Olha esse algoritmo:
- Disco 1 de A pra B
- Disco 2 de A pra C
- Disco 1 de B pra C
- Disco 3 de A pra B
- Disco 1 de C pra A
- Disco 2 de C pra B
- Disco 1 de A pra B
- Disco 4 de A pra C
- Disco 1 de B pra C
- Disco 2 de B pra A
- Disco 1 de C pra A
- Disco 3 de B pra C
- Disco 1 de A pra B
- Disco 2 de A pra C
- Disco 1 de B pra C
Viu? Depois desses passos, todos os discos vão estar na estaca C.

Valeu!! Até a próxima!
Resposta
- Disco 1 de A pra B
- Disco 2 de A pra C
- Disco 1 de B pra C
- Disco 3 de A pra B
- Disco 1 de C pra A
- Disco 2 de C pra B
- Disco 1 de A pra B
- Disco 4 de A pra C
- Disco 1 de B pra C
- Disco 2 de B pra A
- Disco 1 de C pra A
- Disco 3 de B pra C
- Disco 1 de A pra B
- Disco 2 de A pra C
- Disco 1 de B pra C
Exercício Resolvido #6
Elaboração própira
Cinco pessoas precisam atravessar uma ponte numa noite escura, porém, só tem uma lamparina com duração de 30 minutos. Cada uma das pessoas tem um tempo de travessia diferente, e nenhuma consegue atravessar sem iluminação. A ponte só aguenta, no máximo, duas pessoas por vez. Desenvolva um algorítmo que permita a travessia de todos, considerando os seguintes tempos de travessia:

Passo 1
Eai, doido! Olha, vamo começar lembrando que não existe somente uma solução, beleza? Vou te contar uma delas, mas você pode ter uma ideia diferente, até melhor! Fazer igual a mim não é uma regra, ok?

Show! A lâmpada ainda tem 30 minutos de duração. Quem vamos atravessar primeiro?! Eu escolhi atravessar primeiro os dois caras que têm os menores tempos de travessia (1 e 3).

Como ninguém consegue atravessar no escuro, o mais rápido teve que vir no ritmo do cara mais lento. Ou seja, a travessia durou 3 minutos. Com isso, a lâmpada ainda tem 27 minutos de duração. Agora a gente precisa que alguém volte pra buscar outra pessoa. Vamos pro próximo passo então!!
Passo 2
Agora, eu pode ser uma boa a gente voltar com o cara mais rápido, mas na verdade, não faria diferença. Você logo vai ver o porquê.

Agora, a gente pode fazer a seguinte malandragem: deixamos as duas pessoas mais lentas atravessarem juntas, assim eliminando uma viagem demorada. Deixa eu te explicar melhor.
Por exemplo, imagine que o maluco rapidão vá com a senhora de 12 minutos, depois volte, depois vá com a de 8. Essas 3 viagens vão levar 21 minutos no total. Agora, se elas forem juntas, vai levar 12 minutos. Viu? Se as pessoas mais lentas forem juntas, no fim, vai economizar tempo.

Agora, vamos ao próximo passo!
Passo 3
Agora tu já deve ter se ligado no porquê eu quis levar o maluco de 3 minutos primeiro. Olha, agora ele consegue voltar com a lâmpada em 3 minutos pra ajudar o resto da galera! E outra coisa, se eu tivesse primeiro voltado com o maluco de 3 minutos, agora teria que voltar com o de 1 minuto. Ou seja, não faria diferença, beleza?
Show! A gente volta com o doido de casaco:

Ainda nos resta 11 minutos de energia na lâmpada. Repara que os dois mais rápidos estão do mesmo lado, e a gente vai precisar voltar depois. Por isso, é uma boa ideia a gente mandar o mais lento com o mais rápido, pra que o mais rápido consiga economizar tempo na volta.

Ainda nos resta 5 minutos. Mas o maluco rapidão consegue voltar em 1. Então vamos ao próximo passo.
Passo 4
Cara, agora a gente só precisa buscar o doido de casaco que ficou sozinho do outro lado. O Usain Bolt ali vai fazer isso pra gente.

Agora temos 4 minutos restantes. Porém, a travessia desses dois malucos juntos dura só 3 minutos. Com isso, resolvemos nosso problema!!!

Ainda nos restou 1 minuto de bateria. Ufa! Salvamos todo mundo! Hahaha
Valeu, carinha! Até a próxima aventura!

Resposta
- Atravessa A e B
- Volta com A
- Atravessa D e E
- Volta com B
- Atravessa A e C
- Volta com A
- Atravessa A e B
Exercício Resolvido #7
Elaboração própira
O Dexter, mascote do Responde Aí, precisa encontrar uma palavra no dicionário, mas o dicionário tem UM MONTE de palavras. Escreva um algoritmo que ajude o dexter a encontrar a palavra sem ter que ler de uma em uma.
Passo 1
Fala aí, pequeno gafanhoto!! Bom, antes da gente começar a discutir sobre os algoritmos, vamos relembrar que não existe só um algoritmo pra realizar algum trabalho. Existem váaarias respostas pra essa questão, mas também é legal lembrar que o ideal é que a gente tenha o mínimo de trabalho possível, beleza?

Então vamo lá! Vamos supor que você pegou aí um dicionário. Se você simplesmente abrisse ele e fosse lendo palavra por palavra, você encontraria, com certeza, aquela que você procura. Mas tem dois pontos importantes nesse método: se a palavra for com A você vai achar rapidinho, mas se for com Z, aí ferrou.

Imagina que seu dicionário tem 30 mil palavras. No melhor dos casos, você checaria 1 palavra (caso fosse a primeira). No pior dos casos, você verificaria 30 mil fucking palavras (caso fosse a última).

Não é um algoritmo muito bom, né? Realmente, precisamos de uma alternativa. Considerando que o dicionário é organizado em ordem alfabética, olha o passo a passo que eu coloquei aqui embaixo:
- Abrir o dicionário na página do meio e ler a primeira palavra.
- Se a palavra for alfabeticamente maior
- Descartar a parte direita do dicionário e recomeçar o algoritmo
- Se a palavra for alfabeticamente menor
- Descartar a parte esquerda do dicionário e recomeçar o algoritmo
Viu? Quando esse algoritmo chegar no fim, significa que você encontrou a palavra. Esse algoritmo, baseado na subdivisão de um conjunto ordenado de dados é chamado de Busca Binária.

Olha como ficaria, matematicamente:
![]()
Ou seja, você vai dividir tudo por dois até sobrar só uma, que é a que você procura. O n é a quantidade de vezes que a gente precisa dividir por dois. Pra gente descobrir ele, vamos resolver a equação:
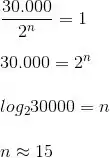
Olha que doideira! Com esse método, no pior dos casos você só precisa ler 15 (QUINZE) palavras. No melhor dos casos, continua sendo 1. Viu a trabalheira que a gente evitou, só parando pra pensar num algoritmo??

Beleza, terminamos! Hahaha valeuuuu!
Resposta
- Abrir o dicionário na página do meio e ler a primeira palavra.
- Se a palavra for alfabeticamente maior
- Descartar a parte direita do dicionário e recomeçar o algoritmo
- Se a palavra for alfabeticamente menor
- Descartar a parte esquerda do dicionário e recomeçar o algoritmo
Exercício Resolvido #8
Elaboração própria
Escreva um algoritmo para perguntar pro usuário uma temperatura em graus Fahrenheit, calcular e responder o valor correspondente em graus Celsius (baseado na fórmula abaixo):
![]()
Passo 1
Fala aí, doido! Pra começar a resolução desse exercício a gente precisa lembrar o que é um algoritmo!

que um algoritmo é uma sequência de instruções que resolvem um determinado problema. Com isso, imagine que você é um programa de computador que faz a conversão entre essas unidades. Nesse caso, o primeiro passo que nós temos que fazer é “perguntar” pro usuário quantos graus fahrenheit ele quer que a gente transforme. Com isso, nosso primeiro passo é perguntar para o usuário!
Passo 2
Beleza! Agora que a gente já sabe o valor em Fº, temos que seguir uns passos pra fazer a transformação. Agora, bora colocar esse valor na nossa fórmula.
![]()
Olha, antes de começar a escrever essa parte no nosso algoritmo, bora lembrar que a gente quer achar o C dessa fórmula, e temos o F. Com isso, o ideal é a gente isolar o C na fórmula. Ficaria +/- assim:
![]()
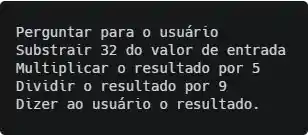
Agora que a gente já perguntou o F, vamos fazer com ele o passo a passo que retorna o valor de C, ou seja, vamos aplicar a fórmula. Os passos são:
- Subtrair 32 do valor de entrada
- Multiplicar o resultado por 5
- Dividir o resultado por 9
Beleza! Fizemos etapas numa cajadada só! Falta só o último passo. Vamo lá!

Passo 3
Se liga, o exercício diz que a gente tem que dizer pro usuário o resultado da conta depois que a gente fizer, então esse é o nosso próximo passo: dizer ao usuário o resultado.

Juntando tudo, a gente fica com:
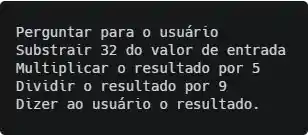
Por enquanto é isso, doido. Valeuuuu!
Resposta