Equação de Nernst
Produzido por Juliana EcheniqueTeoria
Opaa, vamos lá, direto e reto!
A equação de Nernst tem essa carinha aqui:
Opaaa, peraí!!! O que é esse monte de coisa?!
Vamos primeiro as constantes.. .O é a constante de gases ideais ( e o é a constante de Faraday ().
O é o potencial padrão, que a gente calcula usando aquela tabelinha de potencial de redução, ele não é bem uma constante porque vai variar de acordo com a reação, mas é um valor tabelado então não precisa se preocupar!
A temperatura é representada pelo e presta atenção, a unidade é !! O é o número de mols envolvidos na reação e é a constante de equilíbrio da reação.
Equação Simplificada
Se as constantes e vão sempre estar lá, porque não substituir os dados logo? E esse ai, a gente pode passar pra logarítimo na base , não podemos?
Além disso, na maior parte das vezes a gente vai supor condições ambientais, onde a temperatura é ou melhor e , sempre que estivermos nessa situação, podemos usar a equação simplificada:
Agora vamos ver como isso funciona na prática! Vamos calcular o potencial da seguinte pilha:
No lado direito temos o cobre se oxidando e do lado esquerdo o íon de prata que esta se reduzindo, podemos escrever as semi-reações e seus potenciais padrão:
Como o cobre esta se oxidando, a gente inverte a semi-reação do cobre e multiplicamos a semi-reação da prata por dois para podemos escrever a reação global:
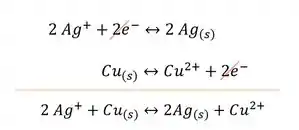
O potencial padrão a gente calcula:
Substituindo:
E a constante de equilíbrio, ?
As concentrações dos íons a gente conhece e quando a gente tem um sólido a gente substitui por , se fosse um gás a gente substituiria pela sua pressão parcial!
Ficamos com:
Substituindo os dados:
Calculando, achamos:
E é só isso!!!
O sinal positivo confirma que estamos falando de uma pilha!
Potencial do eletrodo
Tem uma outra forma de fazer esses cálculos, nela ao invés da gente calcular o da célula inteira a gente usa a equação de Nernst para calcular o de cada eletrodo e só depois calcularmos o do sistema!
O resultado tem que ser o mesmo! Pra te provar isso, a gente vai fazer o mesmo exemplo e vai chegar no mesmo resultado, beleza?!
Primeiro vamos a semi-reação do cobre:
Substituindo na equação de Nernst fica assim:
Viu a diferença?! O é o potencial padrão da semi-reação, que a gente encontra tabelado e o número de mols são os elétrons envolvidos, calculando a gente acha:
Agora vamos fazer a mesma coisa pra a outra meia célula:
Substituindo:
Reparou que o número de mols muda?! Agora calculando a gente acha:
Agora, pra acharmos o potêncial da pilha, fazemos:
Substituindo:
Viu, o mesmo resultado!
Potencial do eletrodo
Exercícios Resolvidos
Exercício Resolvido #1
Escreva a equação de Nernst para a pilha abaixo:
Passo 1
Se a gente considerar a temperatura de , a equação de Nernst tem essa carinha aqui:
Pra a gente escrever a equação de Nernst para essa equação, precisamo descobrir quem é e escrever o !
Para descobrirmos o número de elétrons envolvidos, vamos reescrever a reação colocando seus NOXs:
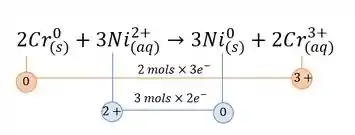
Então a gente tem !
O é nada mais nada menos do que a constante de equilíbrio, ela é a razão entre a concentração dos produtos e dos reagentes elevada ao seu índice, assim:
Só que a gente não considera a concentração dos sólidos, portanto sempre que aparecer um sólido, você multiplica por :
Podemos então escrever a equação:
É só isso!!
Resposta
Exercício Resolvido #2
Lista UFSF
Calcule o para a seguinte pilha:
Dados: ; .
Passo 1
Queremos calcular o da pilha de zinco e cobre, o problema nos da a representação da pilha. Temos a oxidação do zinco e a redução do cobre, então podemos escrever as semi reações e a reação global:
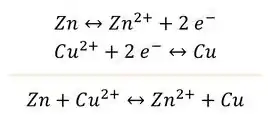
Nesse caso, como a temperatura não é , não podemos usar aquela equação simplificada.
Vamos de equação raiz mesmo!!
O é dado por:
Então ficamos com a seguinte equação:
Passo 2
Para calcular o , fazemos:
Substituindo:
Passo 3
O a gente pode ver nas semi reações acima e ele é igual a e com isso podemos substituir os dados:
Calculando:
Prontinho!!!
Resposta
Exercício Resolvido #3
Para os eletrodos abaixo, considerando e concentração de calcule os seus potenciais:
Passo 1
O problema pede pra a gente calcular os potenciais dos eletrodos e , nesse caso podemos usar a equação de Nernst simplificada!!!
Vamos começar com a reação de redução da prata:
Para a equação de Nernst:
Temos um mol de elétrons envolvido na reação, portanto , substituindo os demais dados:
Agora é só calcular:
Passo 2
Agora vamos para a próxima reação:
A equação de Nernst fica assim:
Substituindo o portencial padrão e a concentração de :
Calculando:
Passo 3
Pra acabar, temos a reação de redução do alumínio:
Substituindo na equação de Nernst:
Achamos:
Resposta
Exercício Resolvido #4
UFC-2010
(Adaptado) O é um dos parâmetros físico-químicos utilizados no monitoramento ambiental de lagos e rios. Este parâmetro pode ser medido experimentalmente montando-se uma célula galvânica com um eletrodo de hidrogênio , sendo a pressão do gás hidrogênio igual a , e com um eletrodo de calomelano , com a concentração de cloreto igual a .As semirreações e os respectivos valores de potenciais de eletrodo padrão para os dois eletrodos são dados abaixo. Se o potencial de eletrodo da célula medido experimentalmente a foi de , calcule o da solução aquosa.
Passo 1
O problema da pra a gente as semi reações da reação de oxirredução e pede pra a gente calcular o da solução aquosa.
Mas antes de qualquer coisa, vamos escrever a reação global. O problema diz que o cátodo é o eletrodo de calomelano e o ânodo é o eletrodo de hidrogênio, portanto o hidrogênio esta oxidando enquanto o mercúrio esta sofrendo redução!
Logo vamos precisar inverter a semi reação de redução do hidrogênio:
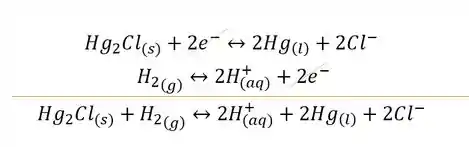
Podemos calcular o potêncial padrão da célula:
Substituindo:
Passo 2
Já sabiamos o potencial da célula e agora também sabemos o seu potêncial padrão, !
Pra achar o da solução a gente vai usar a equação de Nernst:
Para essa reação ela fica assim:
A gente sabe os seguintes dados:
Substituindo:
Usando a propriedade de potência do logarítimo:
Ok, agora presta bastante antenção!!!
A gente quer o , e ele é igual a , a gente já ta de cara pro gol, só precisamos dar uma arrumadinha:
Agora podemos substituir:
Isolando o :
Lembrando que, então é só substituir e...
O da solução vai ser igual a !!!!
Resposta
Exercício Resolvido #5
ITA-2015/2016
Considere a reação descrita pela seguinte equação química:
Sendo X o potencial padrão da reação, o da solução a quando o potencial da reação for será dado por
Passo 1
Hãaam??!!
Relaxa, vamos com calma destrinchando cada partezinha...temos uma reação de oxirredução, então vamos ver quem ta reduzindo e quem ta se oxidando!!
Para isso vamos reeescrever a equação deixando claro o NOX de cada elemento, tanto na direita quanto na esquerda:
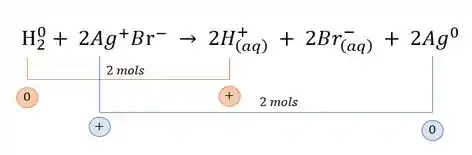
Agora vamos ver o que o problema realmente quer....
Ele ta pedindo o da solução quando e e !
Então a gente vai usar a equação de Nernst, simplificada:
Para essa reação, ela vai ficar:
Aqui é a pressão parcial do , já que ele esta em estado gasoso!
E tem uma galerinha ai que é sólida, então podemos tirar eles, ficamos com:
Passo 2
Como a gente viu lá em cima, temos dois mols de elétrons envolvidos na reação e o problema também nos da
Olhando a estequiometria da reação, temos:
Substituindo:
Usando a propriedade de potência do logaritimo:
Passo 3
Agora vem o pulo do gato!!!!
O problema quer o e ele é dado por:
Podemos dar uma arrumadinha da equação:
Aweee, agora sim! Substituimos o pelo e aproveitamos para dar uma simplificada na equação:
Passo 4
Agora podemos substituir e , ficamos com:
E é só isolar o :
Olhamos as opções que o problema dos da e...
A resposta é a letra (d)!
Resposta
Letra (d).