Análise de variâncias
Produzido por Juliana EcheniqueTeoria
Introdução
Imagine que seu professor de química analítica pediu para você e mais quatro colegas fazerem a determinação de em uma amostra, cada aluno fez suas análises em triplicata e apresentou os valores ao professor.

Após ver os resultados, o professor faz um questionamento à turma: as cinco médias amostrais encontradas por vocês são equivalentes?
Para responder essa pergunta, você e seus colegas precisarão fazer uma análise de variâncias, também conhecido com ANOVA. Os métodos de ANOVA servem para testar se as médias populacionais encontradas pelos alunos podem ser consideradas equivalentes através da comparação de suas variâncias.
Conceitos importantes
Como acabamos de ver, os métodos ANOVA servem para determinar se as médias de uma certa quantidade de séries de dados são equivalentes, ou em outras palavras, mostrar que os valores encontrados estão dentro de um mesmo intervalo de confiança dado um certo nível de confiança.
E a nossa hipótese nula é para provar exatamente isso, que a média populacional dos dados que cada aluno encontrou é a mesma.
Em ANOVA chamamos a diferença entre as séries de dados de fator. Por exemplo, no caso da determinação da acidez feita por você e seus colegas, o fator é o analista. O que difere uma série de dados da outra é apenas a pessoa que fez a análise. Se você tivesse feito cinco triplicatas com métodos diferentes, o fator seria considerado o método utilizado.
Os diferentes valores do fator são chamados de níveis. Como no exemplo temos cinco analistas diferentes, teremos cinco níveis. Cada uma das séries de dados é chamada de grupo.
Para fazer a ANOVA teremos que comparar a variância dentro dos grupos com a variância entre os grupos. Além disso, a para o nosso estudo em química analítica, será interessante aprender apenas o método de ANOVA com um fator. Os métodos para ANOVA com múltiplos fatores podem ser encontrados em livros de estatística avançada.
ANOVA com fator único
Como vimos acima, a ANOVA relaciona as variâncias de dentro dos grupos, com as variâncias entre os grupos. A partir de agora, começaremos a ver uma receitinha para fazer essa comparação e no fim poderemos afirmar se as médias são equivalente ou não.
O primeiro passo, será calcular a média de todos os dados. Isso pode ser feito simplesmente somando todos os dados disponíveis e dividindo pelo número total de amostras, ou fazendo média ponderada das médias de cada grupo:
Pro nosso exemplo, a essa média geral seria:
Em seguida, devemos calcular a soma dos quadrados dos erros devido ao fator (SQF), ou seja, o quadrado dos erros da média de cada grupo com a média geral.
Para o nosso caso dos alunos no laboratório do professor, ficaria assim:
O próximo passo é calcular a soma dos quadrados dos erros (SSE) dentro de cada grupo, ou seja, o quadrado da diferença entre um valor e a média dentro do seu próprio grupo:
Esse é mais complicadinho né, vamos calcular para o nosso exemplo com o auxílio dessa tabela:
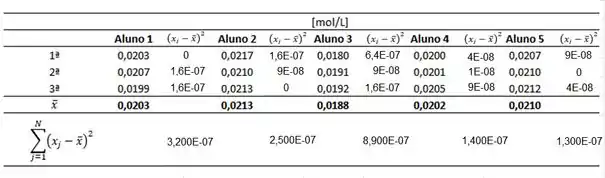
Para cada grupo, calculamos a soma dos quadrados dos erros dentro do próprio grupo, e agora podemos somar tudo:
A soma dos quadrados dos erros, também pode ser calculada usando a variância de cada grupo:
Também é possóvel calcular a soma total dos quadrados:
Uma coisa muito importante é saber o grau de liberdade de cada uma dessa somas. O grau de liberdade da soma dos quadrados devido ao fator é igual ao número de grupos menos 1.
Já o grau de liberdade da soma dos quadrados devido ao erro é igual ao número total de dados menos o número de grupos.
No caso dos estudantes analisando a acidez da amostra fornecida pelo professor, o grau de liberdade do será e do será .
Por fim, o grau de liberdade da soma dos quadrados total é igual a soma dos graus de liberdade SSF e SSE:
Uma vez que calculamos a soma dos quadrados tanto relativos a fator quanto relativos a erro, podemos calcular suas médias dividindo esses valores pelo seu grau de liberdade.
Sendo assim, a média dos quadrados relativos a fator (MQF) é:
E a média dos quadrados relativo a erro (MQE) é:
Depois de fazer tudo isso, você pode respirar aliviado que agora é só calcular F dividindo MSF por MSE:
Vamos calular o valor de para o nosso exemplo então:
Por fim, para sabermos se os valores das médias dos grupos podem ser considerados iguais, ou seja, validar nossa hipótese nula, precisamos comparar o valor de encontrado com os valores tabelados de .
Muito importante: na hora de consultar a tabela você deve lembrar que o grau de liberdade do numerador é e do denominador .
Abaixo, temos um exemplo de tabela F para nível de confiança de .
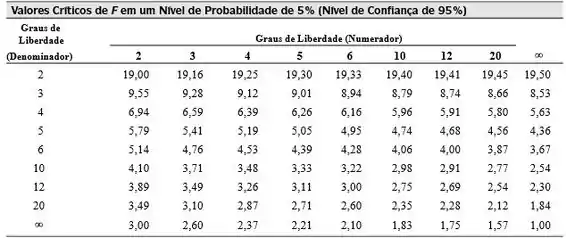
Na tabela, o valor de encontrado para os níveis de confiança e é . Como esse valor é menor que o que encontramos através da metodologia ANOVA, que foi de , a nossa hipótese nula não passou no teste, ou seja, as médias populacionais encontradas pelos alunos não são equivalentes.
O resultado diferente
Se o teste de F não passar, significa que pelo menos uma média não é equivalente às demais. Quando isso acontecer, é possível determinar qual (ou quais) grupo difere dos demais através do cálculo da diferença menos significativa:
Essa fórmula é válida quando todos os grupos têm a mesma população (). Nela, tem grau de liberdade .
Após calcular a menor diferença significativa, devemos comparar as médias dos grupos umas com as outras, aquelas que apresentarem diferença maior que a menor diferença significativa não poderão ser consideradas iguais.
Teste Q
Vamos imaginar que o terceiro aluno, não estava muito confiante com os resultados que ele encontrou e ele quer conferir se um deles pode ser desconsiderado. Para isso, ele pode usar o teste Q, para saber qual resultado descartar.
O teste Q é um teste muito usado para determinar se um certo valor suspeito obtido pode ser descartado ou não.
Para proceder com esse teste, o primeiro passo é colocar todos os valores obtidos em ordem crescente. O teste Q é aplicado sempre nas extremidades, ou seja, com o menor e com o maior valor. Sendo assim, os resultados encontrados pelo aluno 3 em ordem crescente foram: 0, , .
Nesse teste, divide-se a diferença entre o menor/maior valor com o seu vizinho mais próximo pelo tamanho da faixa.
Vamos começar fazendo para o maior valor:
Após encontrar o valor do , ele deve ser comparado com o valor de da tabela abaixo:
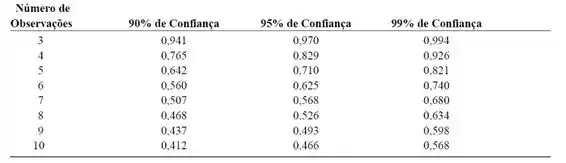
Se , deve-se descartar o valor obtido e recalcular a nova faixa. No nosso caso é menor, então o maior valor não precisa ser descartado.
Fazendo agora para o menor valor:
Para o menor valor, o encontrado é bem mais alto, entretanto, ele ainda está abaixo do valor crítico de para três observações e nível de confiança , portanto ele também não pode ser descartado e o aluno 3 nunca errou em nada que fez na vida.
No teste , quando um valor é descartado, deve-se recalcular a faixa e testar os dois valores da extremidade novamente. Quando tanto o menor valor, quanto o maior valor passarem no teste, significa que todos os valores poderão ser considerados.
ANOVA com fator único
O resultado diferente
Teste Q
Exercícios Resolvidos
Exercício Resolvido #1
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 7, Exemplo 7-11. Adaptado
A análise de uma amostra de calcita gerou porcentagens de CaO de , , , e . Determine se agum valor pode ser rejeitado em um nível de confiança de .
Passo 1
Temos que determinar se todos esses valores estão “ok” ou se tem algum muito discrepante dos outros e que precisa ser decartado. Sendo assim, o teste que precisamos fazer aqui é o teste Q, já que ele é o teste que usamos para aceitar ou rejeitar valores.
Para realizar o teste Q, a primeira coisa que precisamos azer é ordenar os valores obtidos em ordem crescente.

Passo 2
O teste Q sempre é aplicado nas extremidades. Vamos começar então pela extremidade inferior:

Sendo assim, para calcular , devemos fazer:
Ou seja:
Agora, para decidir se o valor deve ser mantido ou rejeitado, precisamos consultar a tabela de valores de Q:
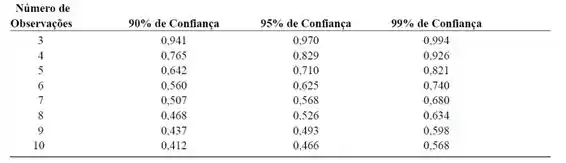
Para um nível de confiança de e cinco observações o valor de é .
Como o teste passou, ou seja, o menor valor dos dados obtidos pode ser aceito.
Passo 3
Agora vamos fazer o mesmo procedimento para a extremidade superior:
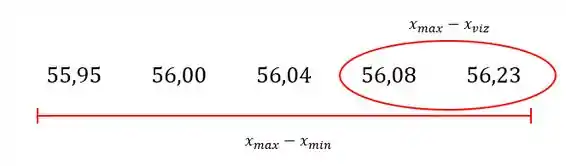
Calculando Q:
Comparando com o valor de que é , o nosso valor de ainda é menor, e portanto o valor máximo também não precisa ser descartado.
Sendo assim, como o teste passou na menor e na maoior extremidade, não existe nenhum valor discrepante e todos valores obtidos podem ser considerados.
Resposta
Devemos manter todos os valores.
Exercício Resolvido #2
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 7, Questões e Problemas 7-31. Adaptado
Aplique o teste Q ao conjunto de dado que segue para determinar se resultados anômalos devem ser mantidos ou rejeitados a um nível de confiança de .
Passo 1
Para saber se os resultados “anômalos”, ou seja, os mais discrepantes devem ser mantidos ou descartados, precisamos aplicar o teste Q.
Para realizar o teste Q, a primeira coisa que precisamos azer é ordenar os valores obtidos em ordem crescente.
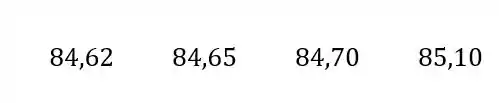
Passo 2
O teste Q sempre é aplicado nas extremidades. Vamos começar então pela extremidade inferior:
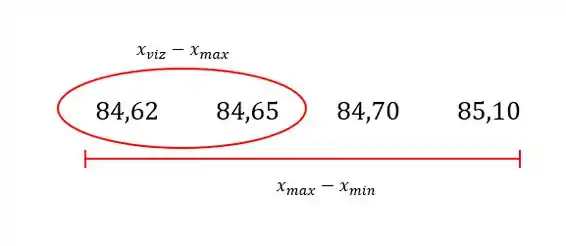
Sendo assim, para calcular , devemos fazer:
Ou seja:
Agora, para decidir se o valor deve ser mantido ou rejeitado, precisamos consultar a tabela de valores de Q:
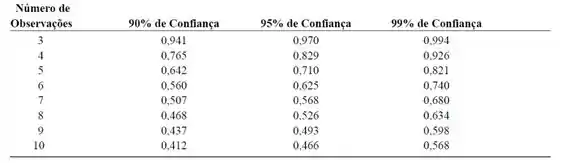
Para um nível de confiança de e quatro observações o valor de é .
Como o teste passou, ou seja, o menor valor dos dados obtidos pode ser aceito.
Passo 3
Agora vamos fazer o mesmo procedimento para a extremidade superior:

Calculando Q:
Comparando com o valor de que é , o nosso valor de ainda é maior, e portanto o valor máximo deve ser rejeitado.
Passo 4
Como o maior valor foi rejeitado, precisamos eliminá-lo e refazer o teste Q com apenas três dados agora:

Calculando o valor de Q para a extremidade inferior:
Para a extremidade superior:
O valor de para três observações e de nível de confiança é .
Ambos os valores de que encontramos é menor que o , o que significa que nenhum outro valor precisa ser descartado.
Como o teste passou tanto na maior quanto na menor extremidade, podemos finalizar o procedimento e considerar os três valores restantes.
Resposta
Apenas o maior valor deve ser descartado.
Exercício Resolvido #3
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 7, Exemplo 7-9.
Cinco analistas obtiveram os resultados (mmol de Ca), mostrados na tabela que se segue, para a determinação de cálcio por um método volumétrico. As médias diferem significativamente em um nível de confiança de ?
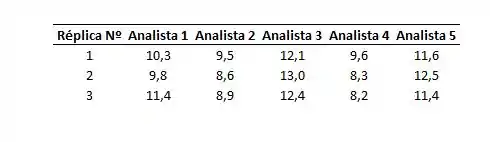
Passo 1
Nessa questão temos cinco séries de dados, e precisamos determinar se as médias populacionais entre elas são iguais, ou seja, precisamos comprovar a hipótese nula abaixo:
Para isso, vamos utilizar um método chamado ANOVA. Esse método analisa a variância de diferentes séries de dados para determinar se elas têm médias populacionais equivalentes
Passo 2
Para começar, precisamos calcular a média aamostral de cada uma das séries.
A média populacional pode ser encontrada através da fórmula abaixo:
Para o primeiro analista, essa média seria:
Para os demais grupos, essa média pode ser encontrada na tabela abaixo:
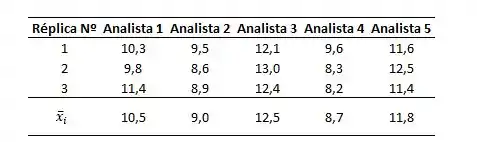
Passo 3
O próximo passo é calcular média total, ou seja, a média de todos os valores obtidos de todos analistas. Essa média pode ser calculada pela seguinte fórmula:
Passo 4
Agora vamos calular o SQF, isto é, a soma dos quadrados entre os grupos. Basicamente precisamos somar os quadrados dos erros da média de cada grupo com a média geral. Só seguir essa fórmula aqui:
A tabela abaixo mostra cada quadrado de fator:
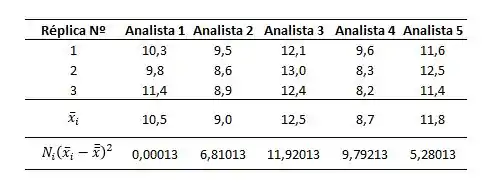
A soma dos quadrados dos fatores será portanto:
Passo 5
O próximo passo é calcilar a soma dos quadrados dos erros, ou seja, a soma dos quadrados dos erros dentro de cada grupo:
Vamos fazer isso com o auxílio da tabela também:
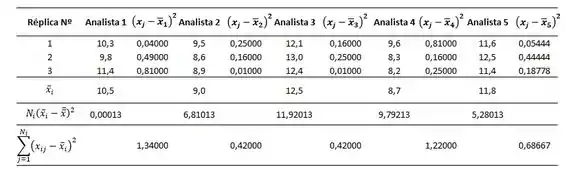
A soma dos quadrados dos erros, será portanto:
Passo 6
O próximo passo é calcular a média dos erro dividindo-os pelo seu grau de liberdade:
Onde é o número total de dados, e é o número de grupos. Portanto:
Passo 7
Estamos acabando finalmente, agora só resta calcular o valor de F e comparar com o F tabelado. Vamos usar a seguinte fórmula para achar :
Vamos então consultar a tabela abaixo para encontrar p valor de e poder comparar:
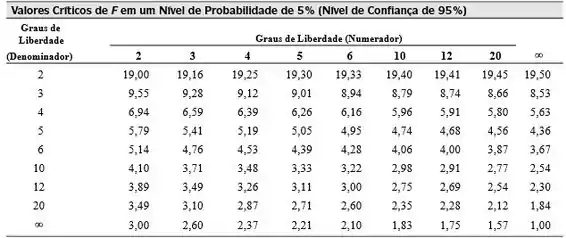
O grau de liberdade do numerador (MQF) é 4, e do denominador (SQF) é 10. Portanto, teremos:
Portanto, o que calculamos é maior que o , isso significa que precisamos rejeitar a hipótese nula, e portanto, existe diferença significativa entre as médias populacionais dos analistas.
Resposta
Existe diferença significativa entre as médias populacionais.
Exercício Resolvido #4
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 7, Questões e Problemas 7-27. Adaptado.
Cinco laboratórios diferentes participaram de um estudo interlaboratorial envolvendo determinações dos níveis de Fe em amostras de água. Os seguintes resultados são réplicas de determinações de ppm de Fe para os laboratórios A-E.
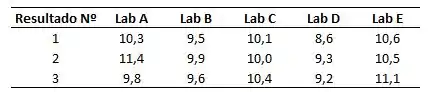
- Defina as hipóteses apropriadas.
- Os laboratórios diferem em um nível de confiança de ? E a um nível de confiança de ()? E ao nível de confiança de ()?
- Calcule a diferença menos significativa para um nível de confiança de
Passo 1
Nessa questão, a mesma análise foi feita por cinco laboratórios diferentes. Precisamos então determinar se as médias populacionais encontradas pelos diferentes laboratórios são equivalentes. Sendo assim, nossa hipótese nula será que todas as médias populacionais são iguais.
A hipótese alternativa, por sua vez, é que pelo menos duas das médias populacionais são diferentes entre si.
Passo 2
Vamos agora então testar nossa hipótese nula. Para fazer isso, devemos primeiro calcular as médias amostrais encontradas.
A média populacional pode ser encontrada através da fórmula abaixo:
Para o primeiro analista, essa média seria:
Para os demais grupos, essa média pode ser encontrada na tabela abaixo:
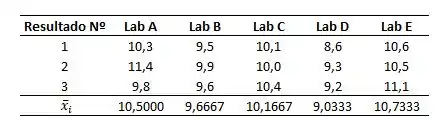
Passo 3
Agora, vamos calcular a média amostral de todos os valores obtidos:
Passo 4
Agora vamos calular o SQF, isto é, a soma dos quadrados entre os grupos. Basicamente precisamos somar os quadrados dos erros da média de cada grupo com a média geral. Só seguir essa fórmula aqui:
A tabela abaixo mostra cada quadrado de fator:
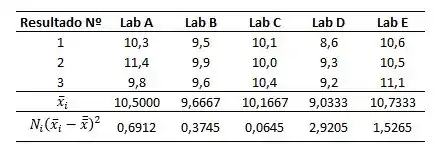
A soma dos quadrados dos fatores será portanto:
Passo 5
Além do SQF, também devemos calcular a soma dos quadrados dos erros, ou seja, a soma dos quadrados dos erros dentro de cada grupo:
Vamos fazer isso com o auxílio da tabela também:
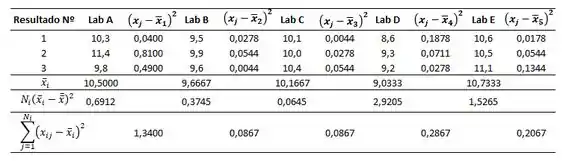
A soma dos quadrados dos erros, será portanto:
Passo 6
O próximo passo é calcular a média dos erro dividindo-os pelo seu grau de liberdade:
Onde é o número total de dados, e é o número de grupos. Portanto:
Passo 7
Estamos acabando finalmente, agora só resta calcular o valor de F e comparar com o F tabelado. Vamos usar a seguinte fórmula para achar :
Vamos então consultar a tabela abaixo para encontrar p valor de para um nível de confiança de e poder comparar:
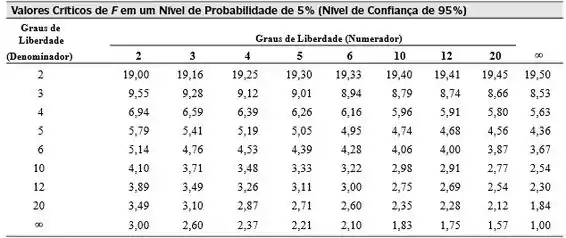
O grau de liberdade do numerador (MQF) é 4, e do denominador (SQF) é 10. Portanto, teremos:
Como , em um nível de confiança de , os resultados não são equivalentes, e a hipótese nula é falsa. Isso é, estamos confiantes de que os laboratórios diferem, vamos verificar agora para .
Para um nível de confiança de , o é de , que ainda é menor que o F encontrado, e portanto a hipótese nula também é falsa nesse nível de confiança. Ou seja, também estamos 99% confiantes de que os laboratórios diferem!
Já para um nível de confiança de , o é , que é maior que o valor de encontrado, e portanto a hipótese nula é verdadeira nesse nível de confiança. Aqui NÃO podemos afirmar com de certeza que os laboratórios diferem.
Passo 8
Para calcular a diferença menos significativa, devemos usar a fórmula abaixo:
Onde tem nível de confiança de e grau de liberdade .
Vamos consultar a tabela abaixo para encontrar esse valor:
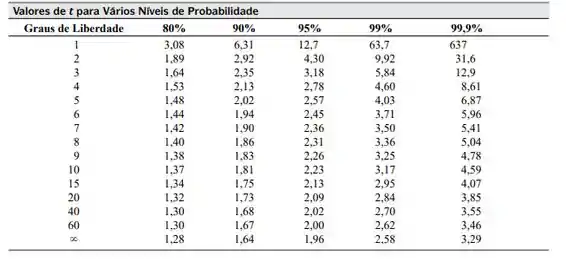
Nela, podemos ver que . Vamos então calcular a MSD:
Onde:
Resposta
- falsa em 95% de nível de confiança
falsa em 99% de nível de confiança
verdadeira em 99,9% de nível de confiança
Exercício Resolvido #5
SKOOG, WEST, HOLLER, CROUCH, Fundamentos de Química Analítica, Tradução da 8ª Edição norte-americana, Editora Thomson, São Paulo-SP, 2006. Capítulo 7, Questões e Problemas 7-30.
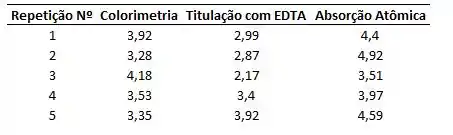
Três métodos analíticos diferentes são comparados em relação à determinação de Ca.Estamos interessados em saber se os métodos diferem entre si. Os resultados, expressos em ppm de Ca, representam determinações por colorimetria, titulação com EDTA e espectrometria de absorção atômica.
a) Defina as hipóteses apropriadas.
b) Determine se existem diferenças significativas entre os três métodos a níveis
de confiança de .
c) Se foi detectada a diferença a um nívelde confiança de 95%, determine quais métodos diferem dos outros
Passo 1
Nessa questão, a mesma análise foi feita através de três métodos quantitativos diferentes. Precisamos então determinar se as médias populacionais encontradas pelos diferentes métodos são equivalentes. Sendo assim, nossa hipótese nula será que todas as médias populacionais são iguais.
A hipótese alternativa, por sua vez, é que pelo menos duas das médias populacionais são diferentes entre si.
Passo 2
Vamos agora então testar nossa hipótese nula. Para fazer isso, devemos primeiro calcular as médias amostrais encontradas.
A média populacional pode ser encontrada através da fórmula abaixo:
Para o primeiro analista, essa média seria:
Para os demais grupos, essa média pode ser encontrada na tabela abaixo:
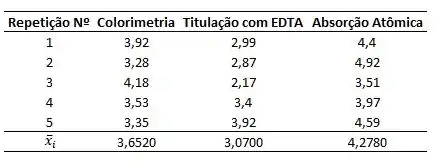
Passo 3
Agora, vamos calcular a média amostral de todos os valores obtidos:
Passo 4
Agora vamos calular o SQF, isto é, a soma dos quadrados entre os grupos. Basicamente precisamos somar os quadrados dos erros da média de cada grupo com a média geral. Só seguir essa fórmula aqui:
A tabela abaixo mostra cada quadrado de fator:
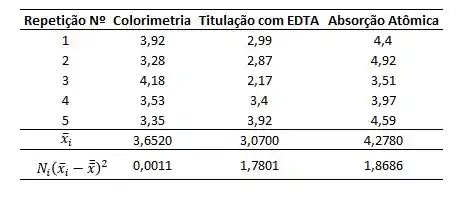
A soma dos quadrados dos fatores será portanto:
Passo 5
Além do SQF, também devemos calcular a soma dos quadrados dos erros, ou seja, a soma dos quadrados dos erros dentro de cada grupo:
Vamos fazer isso com o auxílio da tabela também:
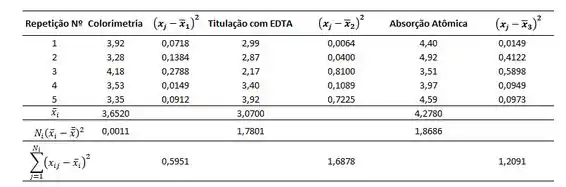
A soma dos quadrados dos erros, será portanto:
Passo 6
O próximo passo é calcular a média dos erro dividindo-os pelo seu grau de liberdade:
Onde é o número total de dados, e é o número de grupos. Portanto:
Passo 7
Estamos acabando finalmente, agora só resta calcular o valor de F e comparar com o F tabelado. Vamos usar a seguinte fórmula para achar :
Vamos então consultar a tabela abaixo para encontrar p valor de para um nível de confiança de e poder comparar:
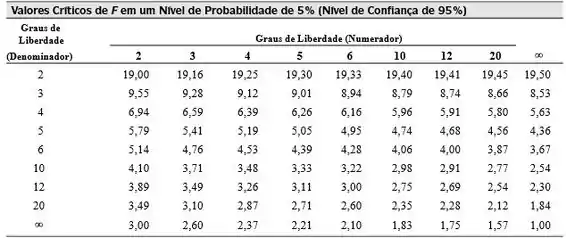
O grau de liberdade do numerador (MQF) é 2, e do denominador (SQF) é 12. Portanto, teremos:
Como , em um nível de confiança de , os resultados não são equivalentes, e a hipótese nula é falsa.
Passo 8
Para saber quais médias populacionais diferem das outras, precisamos primeiro encontrar a diferença menos significativa conforme a equação abaixo:
Onde tem nível de confiança de e grau de liberdade .
Vamos consultar a tabela abaixo para encontrar esse valor:
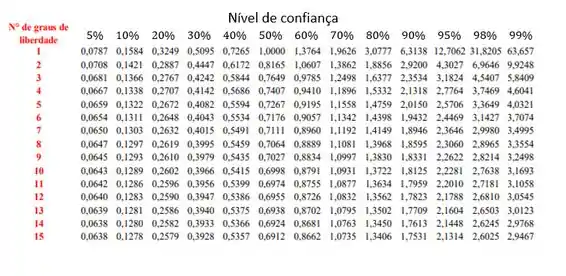
Nela, podemos ver que . Vamos então calcular a MSD:
Onde:
Passo 9
A diferença menos significativa é . Para saber quais médias diferem umas das outras, precisamos encontrar as diferenças entre elas e ver quais são maiores e quais são menores que a DMS.
Através da análise das diferenças entre as médias amostrais dos grupos, podemos ver que o grupo 1 não é significativamente diferente nem do grupo 2 nem do grupo 3. Entretanto, a diferença entre as médias amostrais dos grupos 2 e 3 é maior que a diferença menos significativa, portanto eles são significativamente diferentes.
Resposta
- falsa em 95% de nível de confiança
- Grupos 2 e 3 são diferentes