Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 2.1 - Ex. 103b
Desenhe a estrutura de Lewis mais importante das seguintes moléculas, Mostre todos os pares isoladas e as cargas formais. Desenhe todas as fórmulas de ressonância equivalentes. b)H2CSO
Passo 1
Começando a questão, temos que escrever a estrutura de Lewis da molécula H2CSO. Para isso não podemos esquecer:
-Pares Isolados;
-Cargas formais;
-Ressonância
Mãos a obra
Passo 2
Vamos começar escrevendo a melhor estrutura de H2CSO, como se ela fosse linear, apenas com ligações simples
Agora, podemos completar o octeto das moléculas, vamos começar do elemento menos eletronegativo até o elemento mais eletronegativo.
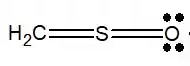
Encontramos a seguinte molécula. Nela percebemos que temos a estrutura desejada. Uau, essa foi fácil, já chegamos na resposta!
Passo 3
Bem, não tão rápido. Você viu que temos um par de elétrons livres e elétrons deslocalizados? Isso mesmo que você está pensando, ainda temos que montar as estruturas de ressonância.
Neste primeiro caso, foi o mais esperado, visto que os elétrons não compartilhados fazem com que a ligação dupla entre em ressonância e crie uma carga negativa no oxigênio. Com isso, temos apenas uma ligação simples e agora, aparece uma carga positiva no enxofre.
Uma segunda opção surge quando a carga negativa passeia pela molécula e agora aparece no Carbono, neste caso, a ligação simples é entre o carbono e o Enxofre. Temos portanto:
Se repararem, chegamos em nossa resposta.
Resposta
