Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 13.1 - Ex. 32
Identifique, na lista a seguir, as reações em que Escreva, para essas reações, as meia-reações balanceadas de oxidação e de redução e oxidação. Mostre que pelo cálculo da a energia livre padrão de Gibbs da reação. Use os menores coeficientes inteiros para balancear as equações.
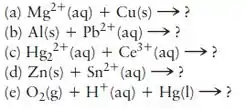
Passo 1
Bora começar mais umaaa!
Pela equação podemos assumir que ela ficará assim:
O que vemos é o se reduzindo a e o oxidando a
Então:
É bom lembrarmos que nas reações espontâneas, , as espécies com potencial mais positivo (ou menos negativo) sofrem redução, enquanto as espécies com potencial menos positivo (ou mais negativo) sofrem oxidação.
Neste caso, quem sofre redução é a espécie menos positiva e, portanto a reação não é espontânea. Ou seja, .
Vamos ver o que acontece na letra b.
Passo 2
Analisando a equação que nos foi dada, podemos deduzir que ela ficará assim:
Nesta reação, é reduzido para enquanto o é oxidado a
Neste caso temos:
O potencial mais positivo é quem reduz aqui, então a reação é espontânea !
Se já sabemos que a reação é espontânea, podemos escrever as meia reações:
Reescrevendo os potenciais padrão:
Se o potencial padrão da célula é:
Substituindo:
Com ente potencial poderemos calcula a energia livre de Gibbs padrão:
Lembrando que:
Substituindo:
Se:
Quando a reação é espontânea, ou seja,
Passo 3
A letra c nós teremos:
Nesta reação, é reduzido para enquanto o é oxidado a
Neste caso temos:
Novamente nós temos o potencial menos positivo sofrendo redução, ou seja, a reação não é espontânea!
Passo 4
Calmaaa! Estamos quase acabando!
Nesta reação, é reduzido para enquanto o é oxidado a
Neste caso temos:
Como a espécie mais positiva é aquela que reduz, então a reação é espontânea, ou seja,
Se já sabemos que a reação é espontânea, podemos escrever as meia reações:
Reescrevendo os potenciais padrão:
Se o potencial padrão da célula é:
Substituindo:
Com ente potencial poderemos calcula a energia livre de Gibbs padrão:
Lembrando que:
Substituindo:
Ou:
Quando a reação é espontânea, ou seja,
Passo 5
Força guerreiros! Estamos na última !
O que pode acontecer aqui é o seguinte:
Nesta reação, é reduzido para enquanto o é oxidado a
Neste caso temos:
Como a espécie mais positiva é aquela que reduz, então a reação é espontânea, ou seja,
Se já sabemos que a reação é espontânea, podemos escrever as meia reações:
Reescrevendo os potenciais padrão:
Se o potencial padrão da célula é:
Substituindo:
Com ente potencial poderemos calcula a energia livre de Gibbs padrão:
Lembrando que:
Substituindo:
Ou:
Quando a reação é espontânea, ou seja,
Ufaaaaa! :P
Resposta
|
|
|