Classificação de Sistemas
Produzido por Alexandre NunesTeoria
O que é controle?
E aí galera, partiu começar a lançar foguetes, criar robôs, controlar a inflação ou impedir que uma doença se propague?
O que que tudo isso tem em comum? Todos esses exemplos são situações que tudo tem que estar dentro do esperado, nada pode fugir muito do ponto onde é esperado que esteja para que não dê um problemão.
Para garantir que as coisas não fujam do controle, existe uma ciência muito bacana chamada “Sistemas de Controle de Processos” e é exatamente isso que vamos começar a aprender e estudar agora. Bora?

Sistema de controle e componentes
O controle de processos acontece através de sistemas de controles de processos. Cada um dos exemplos que eu dei ali em cima é um sistema diferente. Sendo assim um robô tem um sistema de controle para controlar seus movimentos, e um foguete tem um sistema de controle próprio para que ele viaje na inclinação adequada, por exemplo.
Os sistemas de controle são compostos pelos seguintes componentes:
- Processo (ou planta): é o fenômeno que desejamos controlar. Por exemplo: a temperatura de uma peça, o ângulo da articulação do braço de um robô, a tensão elétrica em um capacitor. Será necessário conhecer muito bem o modelo, isto é, a transcrição matemática do nosso processo para que o controle seja bastante eficaz, mas veremos isso mais para frente.
- Controlador: É o chefão, ele recebe uma informação, avalia se é o que ele esperava e manda uma resposta para informar o que fazer.
- Atuador: O braço e perna do sistema, o atuador recebe a resposta do controlador e executa o que ele mandou sobre o sistema a ser controlado. Tá ok, e como que isso ocorre? Os atuadores são os motores elétricos, as bombas, as válvulas entre outros componentes que alteram o estado do sistema a ser controlado.
- Sensor: Esse é o cara que permite perceber o que está acontecendo com o sistema e então retirarmos uma informação para ser comparada com a resposta desejada.
- Exemplo de sensores: acelerômetro, termômetro, extensômetro, entre outros ...ômetros
Sinais
Todos esses componentes precisam conversar entre si, ou seja, é necessário por exemplo que o controlador fale para o atuador o que ele tem que fazer. Essa fofoca é passada através dos sinais. Um sistema de controle tradicionalmente possui os seguintes sinais:
- Sinal de entrada: também chamado de variável de referência, é que o que queremos que aconteça no sistema. Aqui pode ser a posição, velocidade, temperatura, tensão, entre outras variáveis.
- Sinal de saída: como nem tudo são flores, apesar do sinal de entrada ser o que queremos, o sinal de saída pode ser um resultado diferente do que esperávamos. O sinal de saída é uma grandeza física.
- Sinal de realimentação: É a comparação entre o sinal de saída e o sinal de entrada
- Sinal de controle: É o sinal que sai do controlador para o atuador.
A imagem abaixo mostra um tipo de sistema de controle muito usado e que vamos ver muito daqui para frente, o sistema feedback. Essa imagem junta os componentes que vimos ali em cima com os sinais de um sistema de controle em um único diagrama, que chamamos de diagrama de blocos.
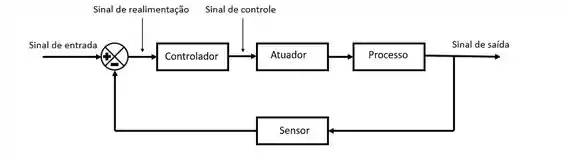
Tipos de controle
Existem dois tipos de sistema de controle, o de malha aberta e o de malha fechada.
Um sistema em malha fechada é aquele que o sinal de saída é realimentado ao sistema. Olhe o diagrama da imagem acima, o sinal da saída volta para o início do diagrama, fechando a malha. Um exemplo clássico do dia-a-dia seria quando você vai tomar banho e quer acertar a temperatura da água do chuveiro. Nesse exemplo a temperatura da água do chuveiro é o sinal de saída, e a abertura do registro é o sinal de entrada. Porém, o tanto que você irá abrir o chuveiro depende da temperatura da água, que é o sinal de saída. Portanto, essa é uma malha fechada.
No sistema em malha aberta o sinal de saída não é realimentado ao sistema, e a entrada é completamente independente da saída. Podemos representar isso num diagrama de blocos da seguinte maneira:
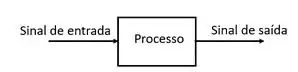
Um exemplo é quando você quer esquentar o seu leite no micro-ondas, o sinal de saída é a temperatura do leite e o sinal de entrada o tempo que você coloca no micro-ondas. Repara que a temperatura final do leite não interfere no tempo que você coloca no micro-ondas no início, você só coloca o tempo lá e torce para o seu leite estar quentinho quando o tempo acabar.
Tipos de sistema de controle
Como eu disse ali em cima, os processos dos nossos sistemas de controle precisam ser matematicamente muito bem conhecidos. Será necessário que os nossos sistemas de controle sejam descritos matematicamente. Uma vez que essas funções matemáticas sejam conhecidas, poderemos então classificar os sistemas de controle em relação a alguns pontos:
A) Sistemas contínuos, discretos no tempo
Sistemas contínuos são o nosso foco, eles são os sistemas cujos sinais de entrada e saída são capazes de mudar em qualquer instante de tempo. Ou seja, tem que existir uma saída para qualquer sinal de entrada.
Logo, um sistema com a seguinte dinâmica:
Teria o seguinte comportamento:
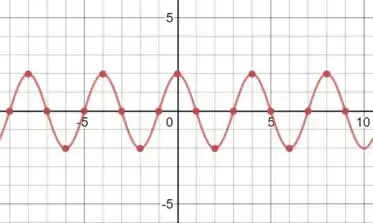
Já os sistemas discretos no tempo são sistemas onde os sinais de entrada e de saída variam pontualmente no tempo, sendo, portanto:
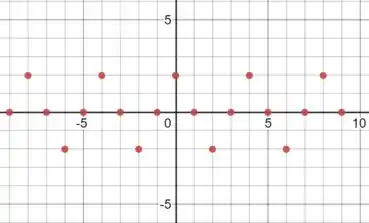
B) Sistemas invariantes e variantes no tempo
Um sistema variante no tempo é um sistema que os seus parâmetros variam no tempo, ou seja, não são constantes.
Uma forma de entender é pegarmos a segunda lei de newton:
Nesse caso, se a massa for constante, ela sai da derivada:
E nesse caso o sistema é invariante no tempo, pois seu parâmetro, no caso a massa, não varia no tempo. Já se a massa não fosse constante, o sistema seria variante com esse formato:
O foguete é um exemplo de um sistema variante no tempo, pois sua massa se altera no tempo devido a queima de combustível.
C) Sistemas lineares e não lineares
Um sistema é linear se a(s) saída(s) depende(m) linearmente da(s) entrada(s) e possíveis perturbações, caso contrário ele é não linear.
Para descobrir isso saber se um sistema é linear ou não, ele deve passar em dois testes:
Vamos aplicar esses testes em duas funções para ver se são lineares ou não.
Primeiramente a função . Aplicando o primeiro teste com e :
Passou no primeiro teste. Vamos para o segundo com e :
`Passou no segundo também, então a função é linear.
Vamos fazer o mesmo procedimento agora para a função
Aplicando o primeiro teste com e :
O primeiro teste já deu errado, ou seja, não é linear.
Além dessas três classificações para os sistemas de controle, existem ainda algumas outras, entretanto, para nós nesse momento, essas que eu apresentei são as mais importantes.
Sinais
Tipos de controle
Tipos de sistema de controle
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Identificar a variável de entrada e indicar o tipo de controle usado em:
- Micro-ondas
- Foguete
- Máquina de lavar roupa
Passo 1
Quando a questão vem assim sem muito detalhes da até um frio na barriga, mas fiquemos tranquilos que não precisaremos de mais informação.
Nessas questões, primeiro nós fazemos uma pergunta, esse sistema poderá garantir uma resposta? Se sim, é um sistema de controle de malha fechada, caso a resposta seja não, o sistema será de controle de malha aberta.
Depois, analisamos o que será usado como referência para poder controlar o sistema.
Vamos ver agora como isso se aplica.
Passo 2
a) Em um micro-ondas, quando vamos usar, nós podemos mexer na potência e no tempo. Contudo, para controle do sistema é utilizado o tempo, logo ele é nossa variável de entrada.
Aqui vai uma dica!!! Normalmente, quando a variável de entrada for o tempo, o sistema será de malha aberta, pois não será possível garantir que a resposta do sistema seja a desejada.
Passo 3
b) Um foguete é um foguete, rs, várias variáveis são utilizadas para que ele realize seu objetivo, sistemas complexos utilizam controle de malha fechada, pois eles precisam garantir a resposta.
Algumas variáveis de entrada no caso do foguete seriam: Aceleração, posição, quantidade de combustível, etc.
Passo 4
c) Caso da máquina de lavar é semelhante ao do micro-ondas, nela colocamos o sabão em pó, amaciante e escolhemos um modo de lavagem, passado algum tempo pré-determinado, vamos lá e retiramos a roupa, ou seja, o resultado do processo, que é a roupa após o processo de lavagem, não interfere nas entradas do mesmo.
Não há como garantir que a roupa estará limpa como desejado, logo é um sistema de malha aberta.
Resposta
- Malha aberta
- Malha fechada
- Malha aberta
Exercício Resolvido #2
Elaboração própria
Classificar os componentes do sistema de controle de malha fechada da velocidade de um carro. Considere os seguintes componentes: passageiro, acelerador, velocidade do veículo, velocímetro.
Passo 1
Então galera, nesse tipo de questão, realizamos uma análise do macro para o micro. E nós fazemos a seguinte pergunta nessa ordem:
O que? Quem? Como? Como?
Primeiro perguntamos o que queremos controlar, depois quem irá promover esse controle.
Encontrado esses dois componentes, partimos para o Como vamos alterar esse sistema (atuador) e em seguida para o Como vamos saber o que está acontecendo no sistema (sensor).
Com essas perguntas respondidas, conseguimos definir o nosso controlador.
Passo 2
Bora lá então, o que queremos controlar? Quando respondermos essa pergunta, teremos a variável de saída do sistema de controle.
Nesse caso, o objetivo principal é que a velocidade do carro seja mantida na faixa desejada, portanto é ela que devemos controlar e é ela que é a variável de saída do sistema.
Mas quem vai promover esse controle? Ora, quem controla a velocidade do carro é o motorista né. Ele que pisa mais ou menos no acelerador, portanto, o motorista é o controlador.
Passo 3
Mas agora como o passageiro controla a velocidade? Pisando mais ou menos no acelerador, como eu disse ali em cima, logo, o acelerador é o nosso atuador.
E como o motorista sabe se ele deve pisar mais ou menos no acelerador? Olhando para o velocímetro e vendo a velocidade atual do carro. Sendo assim, o velocímetro é o nosso sensor.
Resposta
- Controlador: Passageiro
- Atuador: Acelerador
- Sensor: Velocímetro
- Variável de saída: Velocidade do carro
Exercício Resolvido #3
Adaptada de Engenharia de Sistemas de Controle, Norman S. Nise, página 56 Prob. 2
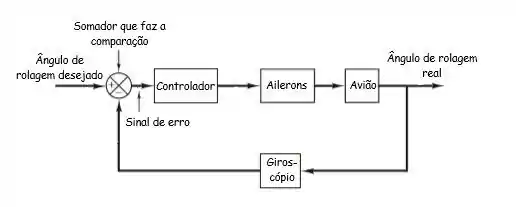
A altitude de uma aeronave varia em rolagem, arfagem e guinagem, conforme definido na figura abaixo. Desenhe um diagrama de blocos funcional para um sistema em malha fechada que estabilize a rolagem da seguinte forma: o sistema mede o ângulo de rolagem real com um giroscópio e o compara o ângulo de rolagem real com o ângulo desejado. Os ailerons respondem ao erro do ângulo de rolagem efetuando um deslocamento angular. A aeronave responde a este deslocamento angular produzindo uma velocidade angular de rolagem.
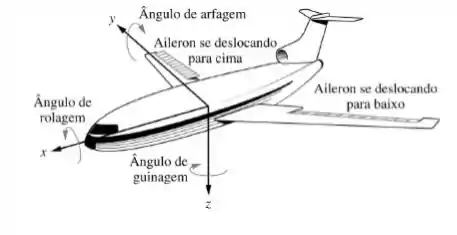
Passo 1
Textão bonito, contudo, o modo de resolver é simples, a mesma lógica desenvolvida nas questões anteriores.
O enunciado já nos diz que se trata de um sistema de controle de malha fechada, que tem uma aparência desse tipo:
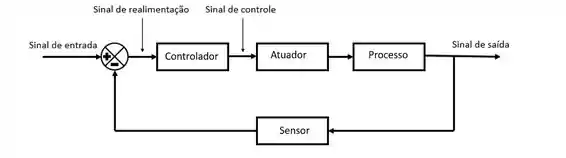
Realizamos uma análise do macro para o micro. E fazemos as seguintes perguntas nessa ordem:
Quem? O que? Como? Como?
Relembrando:
- Quem é o sistema a ser controlado?
- O que queremos controlar nele (variável de referência)?
- Como vamos alterar esse sistema (atuador)?
- Como vamos saber o que está acontecendo no sistema (sensor)?
Com as respostas, conseguimos definir o nosso diagrama de blocos.
Passo 2
Vamos então responder às perguntas!
- O enunciando me diz que o sistema a ser controlado é o avião, o que concorda com nossa lógica de ir do macro para o micro.
- Nos informa que o que se quer controlar é o ângulo de rolagem.
- O que atua para modificar esse ângulo pela descrição do enunciado são os ailerons
- O ângulo de rolagem real é medido através de um giroscópio, logo esse é o nosso sensor.
Com essas informações, conseguimos montar nosso diagrama de bloco.
Passo 3
Colocando cada informação em seu devido lugar resulta nisso:
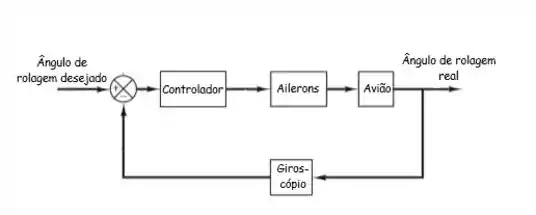
Com tudo onde deveria, ainda fica sobrando informação no enunciado relacionado ao erro do ângulo de rolagem.
Esse erro é justamente a comparação entre o ângulo de rolagem real e o desejado. É em cima desse erro que o controlador vai enviar um sinal para os Ailerons alterarem a dinâmica da aeronave.
Para ficar completo então:
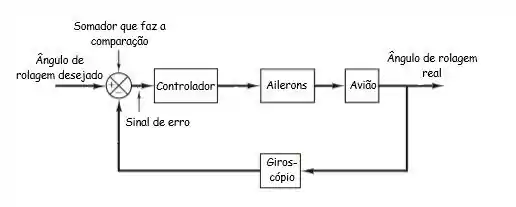
Resposta
Exercício Resolvido #4
Richard C. Dorf e Robert H. Bishop, Sistemas de Controle Modernos, 11ª ed. Rio de Janeiro: LTC., 2009, pg. 23 Prob. P1.2
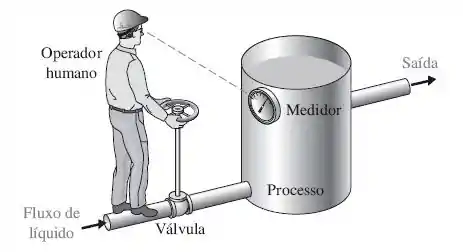
No passado, sistemas de controle usavam um operador humano como parte de um sistema de controle em malha fechada. Esboce um diagrama de blocos do sistema de controle de válvula mostrado na figura abaixo.
Passo 1
O enunciado já nos diz que se trata de um sistema de controle de malha fechada, que tem uma aparência desse tipo:
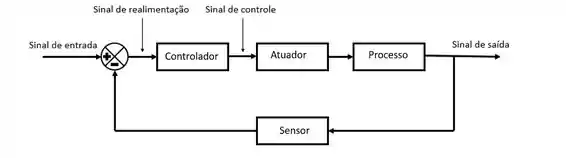
Realizamos uma análise do macro para o micro. E fazemos as seguintes perguntas nessa ordem:
Quem? O que? Como? Como?
Relembrando:
- Quem é o sistema a ser controlado?
- O que queremos controlar nele (variável de referência)?
- Como vamos alterar esse sistema (atuador)?
- Como vamos saber o que está acontecendo no sistema (sensor)?
Com as respostas, conseguimos definir o nosso diagrama de blocos.
Passo 2
Vamos então responder as perguntas!
- A figura nos mostra que o sistema a ser controlado é o processo que ocorre dentro do tanque.
- Notamos pela figura que o que entra no sistema é o fluxo de líquido.
- A forma de alterar o estado desse sistema é através da válvula de controle.
- O nível do tanque é verificado através do medidor.
Com essas informações, conseguimos montar nosso diagrama de bloco.
Passo 3
Colocando cada informação em seu devido lugar resulta:
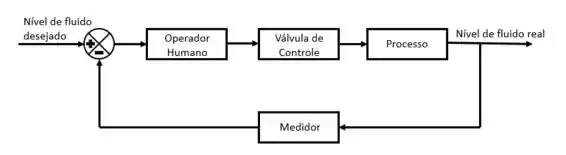
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Richard C. Dorf e Robert H. Bishop, Sistemas de Controle Modernos, 13ª ed. Rio de Janeiro: LTC., 2019, pg. 29 Prob. E1.1
Cite um exemplo dos sensores típicos que possam medir cada um dos seguintes parâmetros:
- Posição linear
- Velocidade
- Aceleração não gravitacional
- Posição rotacional (ou ângulo)
- Velocidade rotacional
- Temperatura
- Pressão
- Fluxo de líquido (ou gás)
- Torque
- Força
- O campo magnético da Terra
Passo 1
Então galera, sensores são instrumentos muito importantes em sistemas de controle. Eles conseguem perceber alterações em alguns desses parâmetros físicos e transmitir essa variação de alguma forma.
Cada um deles é utilizado para uma aplicação específica e podem ser analógicos ou digitais.
Os princípios de funcionamento deles podem ser das mais diversas formas, sendo normalmente escolhidos pela sua sensibilidade, valor e faixa de atuação.
Passo 2
Vamos então responder as perguntas!
A. Posição linear – Extensômetro, GPS.
B. Velocidade – Sensores indutivos, GPS.
C. Aceleração não gravitacional – Acelerômetro.
D. Posição rotacional (ou ângulo) – Giroscópio, GPS.
E. Velocidade rotacional - Tacômetro
F. Temperatura – Termômetros ou Termopares
G. Pressão – Manômetro
H. Fluxo de líquido (ou gás) – Tubo Venturi, rotâmetros, medidor de vazão por pressão diferencial, medidor eletromagnético de vazão, medidor tipo turbina.
I. Torque - Dinamômetro
J. Força – Dinamômetro
K. O campo magnético da Terra – Magnetômetros
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Richard C. Dorf e Robert H. Bishop, Sistemas de Controle Modernos, 11ª ed. Rio de Janeiro: LTC., 2009, pg. 24 Prob. P1.11.
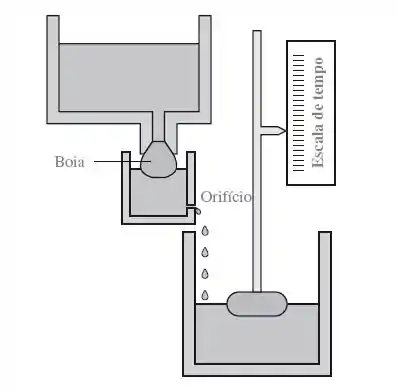
O controle automático do nível de água com boia de nível foi usado no Oriente Médio em um relógio de água. O relógio de água foi usado algum tempo antes de Cristo até o século XVII. Discuta a operação do relógio de água e determine como a boia fornece o controle de realimentação que mantém a exatidão do relógio. Esboce um diagrama do sistema com realimentação.
Passo 1
O enunciado nos diz que esse sistema é um sistema de controle automático, então é um sistema de controle de malha fechada.
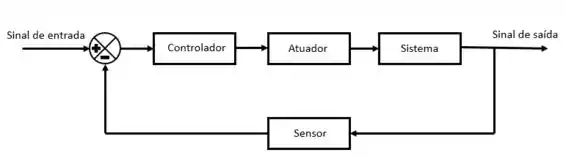
Para sabermos o que é cada caixa desse diagrama, fazemos as seguintes perguntas:
Quem? O que? Como? Como?
Relembrando:
- Quem é o sistema a ser controlado?
- O que queremos controlar nele (variável de referência)?
- Como vamos alterar esse sistema (atuador)?
- Como vamos saber o que está acontecendo no sistema (sensor)?
O interessante dessa questão é que temos menos elementos do que caixas para preencher, ou seja, algumas delas irão ser desconsideradas.
Passo 2
Vamos então a discussão da operação do relógio.
A precisão do relógio depende de um fluxo constante pelo orifício; E o fluxo é dependente do peso da água no tanque intermediário. O peso da água é controlado pela boia.
Logo, a variável controlada por esse sistema é a altura da água.
Erros na medição desse sistema podem aparecer devido ao aumento do furo do orifício e pela evaporação da água no tanque inferior. Mas eles não podem ser corrigidos pelo controlador do sistema que é a boia.
Passo 3
Como citado anteriormente no passo 1, temos menos elementos do que o comum para preencher a caixas do sistema de malha fechada. O que não representa nenhum problema.
Respondendo às perguntas do passo 1 teremos maior clareza.
- Pela discussão da operação do relógio, verificamos que o sistema a ser controlado é o tanque intermediário e dentro dele ocorre um processo que tem que permanecer constante que é o fluxo entre o tanque superior e o tanque intermediário.
- Novamente pela discussão da operação do relógio, a variável controlada é a altura da água no tanque intermediário.
- Não existe atuador mecânico ou elétrico nesse sistema, tudo ocorre através da força gravitacional.
- Não existe um sensor específico nesse sistema. Contudo, existe uma comparação entre a variável de saída, resposta do sistema, e a variável de referência, altura desejada.
Nesse caso posso tanto colocar na caixa referente ao sistema tanto o sistema em si, quanto o processo que está ocorrendo.
Esse tipo de sistema em que não existe um sensor, mas existe comparação entre a variável de entrada e a variável de saída é chamado sistema de controle de malha fechada com realimentação unitária.
Passo 4
No caso desse sistema de controle, somente as caixas referentes ao controlador e ao sistema estarão preenchidas.
O sistema de controle pode ser expresso das seguintes formas:
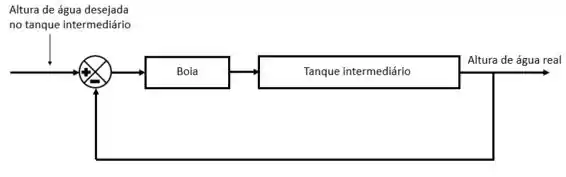
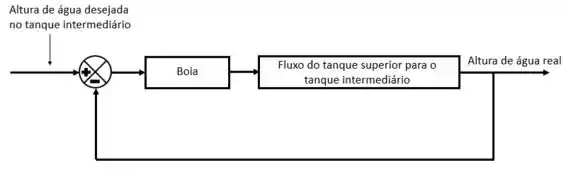
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
USP – P1.2019 – Q.4 – Prof. Hélio Mitio Morishita
A figura abaixo mostra o esquema de um moinho de vento juntamente com suas pás de cauda. O papel da pá de cauda é alinhar o eixo horizontal da turbina eólica (pás principais) com a direção do vento. Pede-se:
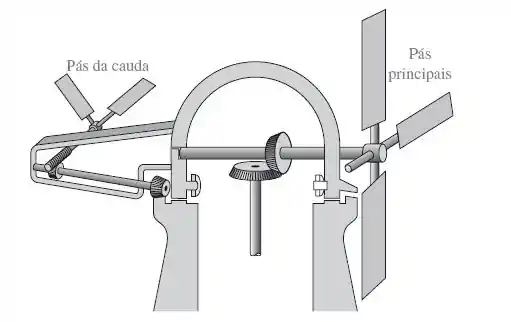
- Analisar a operação do sistema. Este sistema de controle é de malha fechada? Justifica a resposta.
- Propor um diagrama de bloco que sintetiza a dinâmica do sistema, isto é, a dinâmica em função do empuxo gerado nas pás de cauda devido à ação do vento. Justificar a resposta.
Passo 1
Para analisar corretamente a operação do sistema, utilizamos a representação genérica abaixo:
E se ele for capaz de corrigir sua resposta para diferentes variáveis de entrada, então ele é um sistema de malha fechada.
Para propor o diagrama de blocos realizamos as seguintes perguntas:
- Quem é o sistema a ser controlado?
- O que queremos controlar nele e qual a variável de referência?
- Como vamos alterar esse sistema (atuador)?
- Como vamos saber o que está acontecendo no sistema (sensor)?
Passo 2
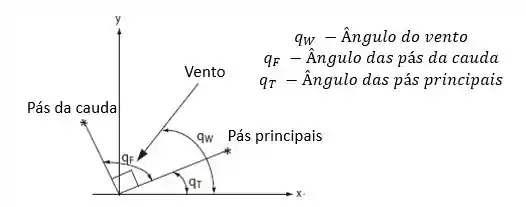
Vamos então a análise de operação deste moinho de vento personalizado 😉.
As pás da cauda, devido ao empuxo do vento, realizam um momento com relação ao moinho que faz a diferença entre o ângulo do vento e o ângulo das pás principais, diminuírem.
Essa diferença é conhecida como erro.
Ou seja, toda vez que o vento variar seu ângulo de incidência, o sistema tende a se reorientar para diminuir essa diferença.
Como o sistema tem o comportamento de corrigir sua resposta, ele é um sistema de controle de malha fechada.
Passo 3
Respondendo às perguntas do passo 1:
- Pela análise da operação do moinho, verificamos que o sistema a ser controlado são as pás principais.
- A variável a ser controlada é o ângulo das pás principais e a variável de referência é o ângulo do vento.
- O atuador mecânico vai ser o torque gerado nas pás principais que vai diminuir a diferença .
- Não existe um sensor nesse sistema como por exemplo um anemômetro. Contudo, existe uma comparação entre a variável de saída, ângulo das pás principais, e a variável de referência, ângulo do vento.
Como as pás da cauda são o controlador e ao mesmo tempo o atuador, em vez de duas caixas, uma para o controlador e outra para o atuador, no nosso diagrama de bloco vai existir uma caixa representando as duas.
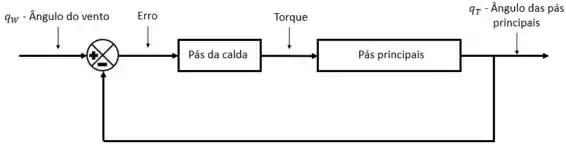
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
USP – Lista 1 – agosto/2017 – Prof. Hélio Mitio Morishita
Verificar se cada uma das funções abaixo são lineares:
a);
a);
c)
Passo 1
E aí galera, tudo tranquilo?
Quando a questão pede para verificar uma função é linear, precisamos aplicar ou o princípio da superposição e da homogeneidade.
Que nada mais é que:
Agora só aplicar em cada uma das funções.
Passo 2
a) Para verificarmos se ; é linear, verificamos se ela satisfaz a seguinte propriedade:
Ou seja,
Logo, , não é linear.
Passo 3
b) Sendo ,para verificarmos se é linear, conferimos se ela satisfaz a seguinte propriedade:
Em casos confusos como esse, uma boa saída é chutar alguns valores e testar se a propriedade não é satisfeita para algum deles.
Considerando e e .
Logo,
Portanto, , não é linear.
Passo 4
c) Verificando a propriedade de superposição e homogeneidade.
Como é uma constante que não dependente de , e os termos são lineares, pois a derivada é um operador linear.
A equação de cima pode ser aberta como:
Que é exatamente:
Logo, a propriedade da superposição e homogeneidade foi satisfeita e é linear.
Resposta
- Não linear
- Não linear
- Linear