Compensadores digitais
Teoria
Introdução
Quando estávamos estudando o controle analógico, nós estudamos um importante elemento dos sistemas de controle que são os compensadores.
Os compensadores, são usados para melhorar algum aspecto da resposta do nosso sistema. Eles podem ser usados para melhorar a resposta transitória, deixando o sistema mais estável e menos oscilatório. Outro uso muito comum dos compensadores é para reduzir o erro em regime permanente.
Lembra como era a função de transferência padrão dos compensadores? Não? Pois ela tá aqui embaixo:
Os compensadores podem ser do tipo avanço de fase ou atraso de fase.
Os compensadores de avanço de fase possuem o zero maior que o polo. Esses compensadores são usados para melhorar a resposta transitória do sistema.
Os compensadores de atraso de fase, por sua vez, possuem os zeros muito menores que o polo. Outra característica desses compensadores é que tanto os polos quanto os zeros são valores bem próximos de . Os compensadores de atraso de fase são usados principalmente para reduzir o erro em regime permanente do sistema.
Os compensadores digitais, por sua vez, vão manter as principais características dos compensadores analógicos. A função de transferência geral dos compensadores digitais será análoga à dos compensadores analógicos, apenas mudando o por .
Como os polos e zeros dos compensadores digitais podem ser positivos, nós vamos usar a expressão geral com “menos” e não com “mais”.
Além disso, os compensadores digitais têm a mesma função no sistema que os compensadores analógicos: melhorar a resposta transitória (avanço), reduzir o erro em regime permanente (atraso). E os métodos para projetar os compensadores digitais são análogos aos métodos para o projeto analógico. Vamos ver melhor como fazer esse projeto?
Compensadores de avanço
Para projetar compensadores de avanço analógicos, nós precisamos de especificações da resposta transitória. Essas especificações geralmente são dadas na forma do overshoot máximo permitido (ou fator de amortecimento, ) e do tempo de decaimento, .
Com e nós devemos calcular o polo dominante, e todo o projeto se dá em torno desse polo dominante. O polo dominante tem a seguinte fórmula:
Para projetar um compensador digital, nós também devemos seguir todos esses passos, e após achar o polo dominante no domínio , devemos transformar esse polo para o domínio .
A demonstração para essa transformação é um pouco chata, então vou pular direto para o que interessa. Para achar o polo dominante no domínio , devemos encontrar o módulo e o ângulo de fase do polo no domínio . Isso pode ser calculado da seguinte fórmula:
Onde é o período de amostragem do sistema.
Sendo assim, após isso teremos o polo dominante no domínio em coordenadas polares:
Por exemplo, se tivermos os polos dominantes no plano :
Sendo assim, teremos:
Podemos calcular então onde esse polo vai se encontrar no plano utilizando as fórmulas ali de cima. Vamos considerar o período de amostragem :
Ou seja:
Mas isso está em coordenadas polares, significo que o polo tem módulo e faz um ângulo de . Graficamente, podemos representar isso da seguinte forma:
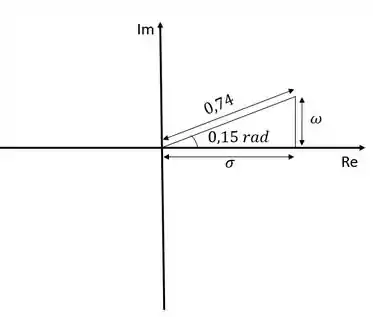
Precisamos passar isso para coordenadas retangulares, ou seja, precisamos encontrar e para conseguir escrever o polo da seguinte maneira:
Podemos fazer isso usando trigonometria:
Para o nosso exemplo teremos:
Portanto:
Dica: essa conversão também pode ser feita usando a função “Rec(“ da sua calculadora.
Em seguida, o projeto do compensador de avanço de fase deve seguir normalmente.
Para nossa felicidade, as regras que usamos no projeto analógico ainda funcionam aqui. Portanto:
Sendo assim, podemos arbitrar um zero e encontrar um zero que garanta que o lugar das raízes passe pelo polo dominante através da regra do ângulo de fase.
Após encontrar o polo e o zero, podemos encontrar o ganho do compensador através da regra do módulo.
Se você não lembra muito bem como utilizar essas regras, seria legal você dar uma olhada na aula de compensadores de avanço. Lá tem tudo explicadinho.
Compensadores de atraso
Para projetar os compensadores de atraso, nós devemos pensar principalmente no erro em regime permanente.
Quando a gente fazia o projeto para o caso analógico, a gente supunha o ganho do compensador como e usava o teorema do valor final para encontrar uma relação entre o zero e o polo:
Onde é o erro em regime permanente desejado e é a constante de erro.
Ao aplicar esse teorema encontramos uma relação entre o polo e o zero, por exemplo:
O próximo passo seria supor um valor bem pequeno para o zero, e calcular o valor do polo usando a relação encontrada acima.
Vamos pensar como podemos adaptar isso tudo para o mundo digital agora.
Primeiramente vamos lembrar da definição da variável :
Sendo assim:
Portanto, para usar o teorema do valor final no domínio , ao invés de fazermos a variável tendendo a , ela deverá tender a .
Portanto, para uma entrada rampa usaremos:
E, para uma entrada rampa:
Onde é a função de transferência do compensador e do processo:
Sendo assim, após aplicar esse teorema teremos algo do tipo:
Onde é uma constante qualquer.
Por exemplo, se temos um processo cuja função de transferência é:
E queremos um compensador que faça com que o erro em estado permanente seja , deveremos primeiramenrte encontrar o que gera esse erro:
Com poderemos encontrar a relação que queremos:
Isso vai nos dar:
E com isso conseguimos continuar o projeto do compensador de atraso normalmente.
Agora só precisamos arbitrar um valor qualquer para o zero e calcular o polo usando a relação que conseguimos através do teorema do valor final acima.
Quando estávamos fazendo o projeto analógico, nós usávamos um valor para o polo bem próximo de . Aqui, como fizemos a mudança para o sinal digital, nós vamos querer que o zero seja o mais próximo de possível. Geralmente é um bom palpite para o zero.
Após isso, basta calcular o ganho do compensador através da regra do módulo:
Compensadores de avanço
Compensadores de atraso
Exercícios Resolvidos
Exercício Resolvido #1
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 13.9. Adaptado
Para entradas em degrau e rampa obtenha o erro em regime permanente para a função de transferência em malha aberta dada abaixo:
Passo 1
Vamos fazer primeira para a entrada degrau.
As fórmulas para o erro da entrada degrau são:
Vamos calcular a constante do erro então:
Calculando o erro:
Passo 2
Vamos agora calcular o erroa para a entrada rampa.
As fórmulas de erro para a entrada rampa são:
Calculando primeiramente o :
O erro será portanto
Resposta
Entrada rampa:
Entrada degrau:
Exercício Resolvido #2
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 13.7. Adaptado
Para entradas em degrau e rampa obtenha o erro em regime permanente para o sistema mostrado abaixo:
Passo 1
O primeiro passo será encontrar a função de transferência do sistema no plano .
No plano temos que:
Precisamos aplicar a transformada na função de transferência, sendo assim:
Manipulando um pouco:
Como pela definição temos que:
Podemos fazer:
Portanto:
Passo 2
Vamos agora expandir em frações parciais para encontrar a transformada desse termo:
Consultando uma tabela de transformada , teremos:
Logo:
Passo 3
Vamos fazer primeira para a entrada degrau.
As fórmulas para o erro da entrada degrau são:
Vamos calcular a constante do erro então:
Calculando o erro:
Passo 4
Vamos agora calcular o erroa para a entrada rampa.
As fórmulas de erro para a entrada rampa são:
Calculando primeiramente o :
O erro será portanto
Resposta
Entrada rampa:
Entrada degrau:
Exercício Resolvido #3
Elaboração própria
Dado a função de transferência em malha aberta abaixo:
É desejado implementar um compensador de avanço de fase que reduza o erro em regime permanente para uma entrada degrau desse sistema em vezes. Para que isso aconteça, qual deve ser a relação entre o polo e o zero do compensador.
Passo 1
Esse exercício quer que a gente determine uma boa relação entre o zero e o polo do compensador de avanço que será implementado para que ocorra a redução de erro em regime permanente desejada para uma entrada degrau.
Para fazer isso, vamos com calma. Primeiramente, vamos calcular o erro em regime permanente para uma entrada degrau desse sistema sem o compensador.
As fórmulas para o erro da entrada degrau são:
Ou seja:
Passo 2
O objetivo é que a compensação reduza o erro em vezes, portanto, o novo erro deverá ser:
E o novo :
Passo 3
A função de transferência do sistema com compensação será:
Portanto, podemos achar a relação entre os polos, calculando o novo :
Portanto:
Resposta
Exercício Resolvido #4
Elaboração própria
Dados os polos dominantes no plano :
Encontre o polo dominante equivalente no plano . Assuma
Passo 1
Bora lá.
Nesse exercício nós temo um par de polos no plano e precisamos definir quais serão os polos equivalentes no plano . Para isso, encontraremos primeiramente o polo em coordenadas polares e em seguida converteremos esse polo para coordenadas polares. Sendo assim, primeiramente o polo dominante em terá a cara:
Sendo que:
Passo 2
A fórmula geral de um polo dominante no plano é:
E o nosso polo é:
Comparando os dois teremos:
Portanto, podemos calcular o módulo e o ângulo do polo no plano :
Portanto, o polo no plano em coordenadas angulares será:
Passo 3
Para encontrar esse polo em coordenadas retangulares, vamos usar a calculadora. Não precisa ser nenhuma calculadora superpoderosa para fazer essa conversão, aquela basiquinha que todo aluno de engenharia tem consegue fazer isso perfeitamente.
Para fazer a conversão você deve apertar o botão “shift” e em seguida o botão “Pol(” ativando assim, a função “Rec(“ da calculadora. Em seguida, digite o valor do módulo que calculamos, aperte o botão da vírgula, digite o valor do ângulo, e feche o parênteses. Certifique-se também de que sua calculadora está no modo “radianos” e não no modo “graus”.
Após fazer isso, aperte igual e aparecerá o valor da parte real no visor, para o nosso caos:
Para encontrar a parte imaginária, pressione a tecla “ALPHA” e em seguida a tecla “tan”. Aparecerá um “F” no visor da calculadora, aí basta apertar igual e aparecerá o valor da parte imaginária no visor. Para o nosso exemplo, esse valor é:
Portanto, os nossos polos dominantes no planos serão:
Resposta
Exercício Resolvido #5
Elaboração própria
Projete um compensador de atraso que faça com que o erro em regime permanente do sistema abaixo seja de para uma entrada degrau.
Passo 1
Vamos primeiro descobrir qual o que faz com que o sistema produza o erro desejado. Para isso, vamos usar a fórmula que relaciona o erro com o :
Para o erro ser :
Passo 2
Agora, com o precisamos encontrar a relação entre o polo e zero do compensador usando a fórmula do próprio :
Onde representa a função de transferência em malha aberta que é o produto da função de transferência do processo com a função de transferência do compensador que estamos projetando. Ou seja:
Obs: Nessa etapa, podemos considerar o ganho do compensador como sendo .
Como o deve ser , teremos:
Fazendo o limite:
Passo 3
Agora que já temos a relação entre o polo e o zero do compensador, podemos arbitrar um dos dois e encontrar o outro.
Para isso, geralmente arbitramos o polo e encontramos o zero. O melhor a se fazer é arbitrar um valor para o polo bem próximo de para que o zero não fique muito longe do polo.
Quanto mais próximos o zero e o polo estão, menor é o impacto do compensador na resposta trtansitória do sistema. Dessa forma diminui-se o erro em regime permanente sem alterar e o tempo de acomodação.
Vamos então arbitrar . Assim teremos:
Dessa forma, a expressão para o compensador será:
Como o polo e o zero estão bem próximos, não há necessidade de se calcular um ganho para o compensador uma vez que este será bem próximo de .
Caso esses valores não fossem tão próximos, ou o rigor do projeto fosse maior, seria necessário encontrar os polos dominantes do sistema sem compensação e depois usar a lei dos módulos para encontrar o ganho do compensador.
Resposta
Exercício Resolvido #6
Elaboração própria
Projete um compensador de atraso que faça com que o erro em regime permanente do sistema abaixo seja de para uma entrada rampa.
Passo 1
Vamos primeiro descobrir qual o que faz com que o sistema produza o erro desejado. Para isso, vamos usar a fórmula que relaciona o erro com o :
Para o erro ser :
Passo 2
Agora, com o precisamos encontrar a relação entre o polo e zero do compensador usando a fórmula do próprio :
Onde representa a função de transferência em malha aberta que é o produto da função de transferência do processo com a função de transferência do compensador que estamos projetando. Ou seja:
Obs: Nessa etapa, podemos considerar o ganho do compensador como sendo .
Como o deve ser , teremos:
Fazendo o limite:
Passo 3
Agora que já temos a relação entre o polo e o zero do compensador, podemos arbitrar um dos dois e encontrar o outro.
Para isso, geralmente arbitramos o polo e encontramos o zero. O melhor a se fazer é arbitrar um valor para o polo bem próximo de para que o zero não fique muito longe do polo.
Quanto mais próximos o zero e o polo estão, menor é o impacto do compensador na resposta trtansitória do sistema. Dessa forma diminui-se o erro em regime permanente sem alterar e o tempo de acomodação.
Vamos então arbitrar . Assim teremos:
Dessa forma, a expressão para o compensador será:
Como o polo e o zero estão bem próximos, não há necessidade de se calcular um ganho para o compensador uma vez que este será bem próximo de .
Caso esses valores não fossem tão próximos, ou o rigor do projeto fosse maior, seria necessário encontrar os polos dominantes do sistema sem compensação e depois usar a lei dos módulos para encontrar o ganho do compensador.
Resposta
Exercício Resolvido #7
Centro Federal de Educação Tecnológica do Paraná – Departamento Acadêmico de Eletrônica – Controle Digital – Professor Brero - Apostila Projeto no Plano z – Exemplo. Adaptado
Dado o sistema realimentado com , projete um compensador digital que atenda às especificações:
Passo 1
O primeiro passo para fazer o projeto no plano é encontrar os polos dominantes no plano e depois convertê-lo ao plano .
O polo dominante no plano terá forma:
O valor de nós já temos que foi dado como especificação de projeto, . Para achar vamos usar a especificação do tempo de assentamento. Para uma faixa de a fórmula para o tempo de decaimento é a seguinte:
Substituindo os valores:
Os polos dominantes no plano serão portanto:
Passo 2
Agora precisamos determinar onde estarão esses polos no plano atravé das seguintes fórmulas:
Portanto, podemos calcular o módulo e o ângulo do polo no plano :
Portanto, o polo no plano em coordenadas angulares será:
Fazendo a conversão de coordenadas polares para retangulares teremos:
Passo 3
Vamos representar os polos dominantes e o polo da função de transferência do processo no diagrama abaixo:
O ponto preto indica o polo dominante em e o “xis” vermelho representa o polo da função de transferência do processo. Agora precisamos encontrar o polo e o zero do compensador. Para isso, podemos simplesmente arbitrar um polo qualquer e então encontrar onde vai estar o zero correspondente.
Como o nosso compensador será de avanço sabemos que o polo tem que estar mais à direita que o zero. Sendo assim, vamos tentar arbitrar o nosso polo um pouco mais à direita do nosso diagrama.
Eu vou escolher simplesmente porque eu quero, mas você poderia ter escolhido qualquer valor para o polo. Sendo assim, vamos representar nosso diagrama agora:
O “xis” azul representa o polo do compensador e o círculo azul o zero. O zero do compensador foi colocado em um lugar arbitrário, sendo assim, precisamos determiner qual é o ponto exato do zero considerando que o polo foi colocado em .
Passo 4
Para determinar o ponto exato do zero, usaremos a regra dos ângulos que diz que a soma dos ângulos dos polos menos a soma dos ângulos dos zeros deve ser igual a um múltiplo ímpar de .
Sendo assim, teremos:
Vamos calcular os ângulos e :
Sendo assim, podemos determinar :
Podemos agora determinar o ponto exato do zero do compensar, já que encontramos o ângulo que ele faz com o polo dominante:
Isso vais nos dar:
Portanto, nosso compensador por enquanto está assim:
Falta apenas calcular o ganho.
Passo 5
Para calcular o ganho, usaremos o critério do módulo. Para isso, precisaremos calcular as distâncias entre os polos dominantes e os polos e zeros do sistema:
Precisamos calcular , e :
A regra do módulo diz que:
Sendo o ganho do compensador e o ganho do processo. Sendo assim:
Sendo assim, calculamos finalmente a função de transferência do nosso compensador de avanço:
Resposta
Exercício Resolvido #8
Exercício 1 – Projeto de compensadores no plano z – Eng Luis Cezar Emanuelli
Considere o sistema de controle mostrado abaixo. No plano , projete um compensador digital que apresente polos dominantes em malha fechada com uma constante de amortecimento e tempo de acomodação para uma faixa de de . O período de amostragem utilizado será .
Passo 1
O primeiro passo para fazer o projeto no plano é encontrar os polos dominantes no plano e depois convertê-lo ao plano .
O polo dominante no plano terá forma:
O valor de nós já temos que foi dado como especificação de projeto, . Para achar vamos usar a especificação do tempo de assentamento. Para uma faixa de a fórmula para o tempo de decaimento é a seguinte:
Substituindo os valores:
Os polos dominantes no plano serão portanto:
Passo 2
Agora precisamos determinar onde estarão esses polos no plano atravé das seguintes fórmulas:
Portanto, podemos calcular o módulo e o ângulo do polo no plano :
Portanto, o polo no plano em coordenadas angulares será:
Fazendo a conversão de coordenadas polares para retangulares teremos:
Passo 3
Vamos representar os polos dominantes e o polo da função de transferência do processo no diagrama abaixo:
O ponto preto indica o polo dominante em , os “xis” vermelho representam os polos e os círculos vermelhos representam os zeros da função de transferência do processo. Agora precisamos encontrar o polo e o zero do compensador. Para isso, podemos simplesmente arbitrar ou o polo ou o zero e depois encontrar o outro usando a regra dos ângulos.
Uma estratégia muito usada nessas situações é arbitrar um polo/zero de forma que ele cancele um polo/zero já existente, facilitando assim o projeto do compensador. Aqui por exemplo, podemos arbitrar o zero do compensador em de forma que cancele com o polo do processo que já existe.
Sendo assim, nosso diagrama ficará:
Repare que o polo em sumiu porque ele foi cancelado com o zero do compensador. O “xis” azul representa o polo do compensador que precisamos determiner em que ponto ficará.
Passo 4
Para determinar o ponto exato do polo, usaremos a regra dos ângulos que diz que a soma dos ângulos dos polos menos a soma dos ângulos dos zeros deve ser igual a um múltiplo ímpar de .
Sendo assim, teremos:
Vamos calcular os ângulos e :
Sendo assim, podemos determinar :
Podemos agora determinar o ponto exato do polo do compensar, já que encontramos o ângulo que ele faz com o polo dominante:
Isso vais nos dar:
Portanto, nosso compensador por enquanto está assim:
Falta apenas calcular o ganho.
Passo 5
Para calcular o ganho, usaremos o critério do módulo. Para isso, precisaremos calcular as distâncias entre os polos dominantes e os polos e zeros do sistema:
Precisamos calcular , e :
A regra do módulo diz que:
Sendo o ganho do compensador e o ganho do processo. Sendo assim:
Sendo assim, calculamos finalmente a função de transferência do nosso compensador de avanço: