Controlador proporcional-derivativo e proporcional-integrativo-derivativo
Teoria
Controlador proporcional-derivativo (PD)
No último tópico vimos como as vezes a introdução de uma parcela integrativa na função de transferência pode ser muito bem-vinda quando queremos cancelar o erro em regime permanente.
Em alguns casos porém, o erro em regime permanente não vai ser o nosso maior problema. Em várias aplicações de controle de processos na vida real, a existência desse erro é tolerável, entretanto, existe um outro problema bastante comum que encontraremos que é a velocidade de resposta do processo.
Por vezes, precisaremos que o sistema responda de maneira bem rápida à ação do controlador. Nesses casos, nós iremos utilizar uma parcela derivativa na função de transferência do controlador.
Ou ainda, no domínio frequência:
Como disse ali em cima, o principal efeito dessa ação derivativa no nosso controlador é acelerar a resposta do sistema a uma perturbação qualquer. Mas como será que isso acontece na prática?
A função principal da ação derivativa é antecipar como o sistema vai reagir e já corrigir essa antecipação, por isso que ele acelera o tempo de resposta. Por exemplo, se a variável controlada estiver se afastando para cima do setpoint a ação diferencial perceberá isso pois a derivada do erro será muito alta, então será tomada uma ação mais rigorosa.
Agora, caso a variável de processo esteja se aproximando do valor de referência lentamente, a derivada do erro será muito baixa, aí nesse caso a ação da parcela diferencial do controlador será praticamente nula.
Podemos então perceber que a ação derivativa é muito importante para corrigir desvios em variáveis que variam muito rapidamente, fazendo uma previsão do que acontecerá com o sistema e tomando as devidas medidas para evitar que essas variações continuem acontecendo
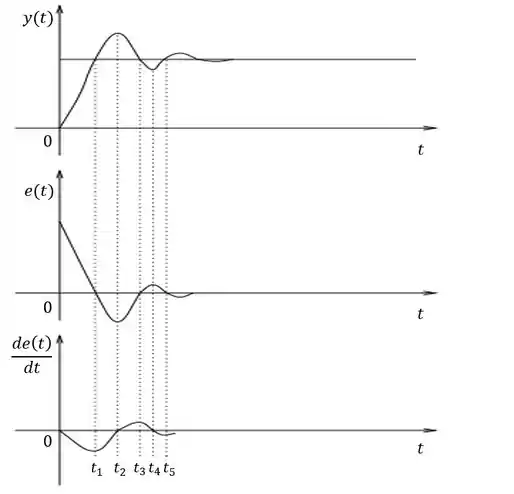
A figura acima mostra graficamente como a ação diferencial do controlador. Repare por exemplo que para a variável do processo, estava abaixo do valor final, entretanto o que mostra que a ação diferencial estava reduzindo o sinal de saída do controlador pois antecipou que em pouco tempo a variável de processo ultrapassaria o valor desejado.
Controlador proporcional-derivativo modificado
Na vida real, entretanto, o controlador PD muito raramente é introduzido com a equação que vimos ali em cima. Na verdade, ele sofre uma pequena alteração:
O que acontece é que a parte derivativa da equação de transferência é multiplicada pelo termo .
Esse termo é chamado de filtro, e ele tem a forma de um processo de primeira ordem com constante de tempo . Geralmente utiliza-se valores muito baixos de (valores variam entre e dependendo do fabricante) de modo a deixar o processo mais lento e o polo criado bem afastado da origem.
O filtro é necessário pois a ação derivativa pura é extremamente sensível em altas frequências ( muito grande) fazendo o ganho do sistema tender ao infinito. O termo do filtro, por ter um polo em alta frequência faz com que o sistema fique controlado nessa região.
Então combinaremos assim, quando estiver falando de controladores com ação derivativa, teremos duas funções de transferência característica. A do controlador PD ideal:
E a do controlador PD real:
Controlador proporcional-integrativo-derivativo (PID)
Nós já vimos anteriormente que o controlador proporcional é o mais simples, barato e usado de todos os tipos de controladores. Vimos que quando precisamos remover o erro em regime permanente a nossa melhor opção é adicionar um termo integrativo ao nosso controlador. E que, quando precisarmos de um sistema mais rápido e mais estável, a adição de um controlador com um termo derivativo será a melhor pedida.
Os controladores PID, portanto, são os mais complexos, e robustos controladores encontrados no mercado. Eles reúnem a parte proporcional, integrativa e derivativa no mesmo controlador. Ou seja, ele será eficaz para praticamente todos os processos que podemos encontrar. Entretanto, alguns processos são muito simples e o uso de um PID não é justificado. Seria como usar um canhão para matar uma formiga hahaha.
A equação para o sinal de saída do controlador PID pode ser escrita como:
Se fizermos a transformada de Laplace para obter a função de transferência:
O termo integrativo será então o responsável por cancelar o erro em regime permanente e é muito importante para garantir a precisão do sistema.
O termo derivativo está ligado à estabilidade e rapidez da resposta devido ao seu efeito antecipatório. Ele é muito importante visto que o efeito integrativo causa uma certa instabilidade no sistema e por isso, o efeito derivativo acaba se tornando mais importante ainda.
Mas fica de olho. Às vezes, a função de transferência pode vir escrita de uma forma diferente:
Alguns livros e apostila de controle de processos adotam essa fórmula para descrever um PID. Ela é a mesma coisa da que eu escrevi anteriormente, porém as constantes estão representadas de forma diferente. Nessa nova convenção:
Além disso, como vimos na seção anterior, sempre que tivermos o efeito derivativo no nosso controlador, faremos uso do filtro para reduzir a instabilidade do sistema em altas frequências. Então, assim como o controlador PD tinha sua versão real e a ideal, o controlador PID também terá.
Controlador PID ideal:
Controlador PID real:
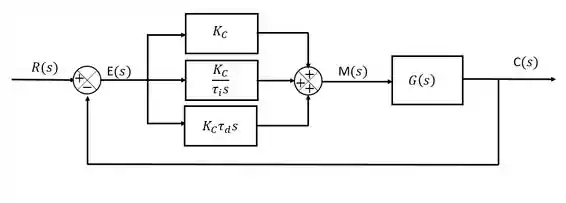
Representando o controlador PID no diagrama de blocos com cada ação representada separadamente, teremos algo do tipo:
Controlador proporcional-derivativo modificado
Controlador proporcional-integrativo-derivativo (PID)
Exercícios Resolvidos
Exercício Resolvido #1
IF-RS - 2015 - IF-RS - Professor - Controle, Automação e Instrumentação Industrial.
Considerando as afirmações abaixo sobre ações de controle de processos (on-off, Proporcional, Integral, Derivativa) e suas combinações:
I. Este tipo de controle combina características de estabilidade com eliminação do erro em um único controlador. Faz com que o sinal de erro seja minimizado pela ação proporcional, zerado pela ação integral e obtido em uma velocidade antecipada pela ação derivativa. É indicado para processos nos quais a dinâmica dominante é de segunda ordem.
II. Este controle normalmente é empregado em processos que podem admitir certa oscilação contínua da variável de controle em torno do valor desejado. São exemplos de instrumentos utilizados neste tipo de controle os pressostatos, termostatos e chaves de nível.
III. Este controle elimina o erro de forma automática gerando uma resposta transitória adequada pela ação proporcional.
IV. Este tipo de controle fornece uma saída proporcional ao erro permitindo o ajuste do ganho ou da banda proporcional pelo operador, de modo que o erro possa ser compensado.
V. Este tipo de controle, na prática, não pode ser utilizado isoladamente, porém, ao ser utilizado com outro tipo de controle, melhora a estabilidade do sistema.
Assumindo que “P” representa ação proporcional, “I” a ação integral e “D” a ação derivativa. Assinale a alternativa que relaciona as afirmações, na ordem em que foram apresentadas, com sua respectiva ação de controle.
- PID, On/Off, PI, P, PD.
- PD, On/Off, P, PI, PID.
- PID, PD, PI, P, On/Off.
- PI, On/Off, P, PID, PD.
- PID, On/Off, PD, P, PI.
Passo 1
Vamos analisar cada um dos itens e tentar adivinhar de qual controlador ele tá falando.
I. Este tipo de controle combina características de estabilidade com eliminação do erro em um único controlador. Faz com que o sinal de erro seja minimizado pela ação proporcional, zerado pela ação integral e obtido em uma velocidade antecipada pela ação derivativa. É indicado para processos nos quais a dinâmica dominante é de segunda ordem.
Esse controlador aí aparentemente tem tudo né. O erro é minimizado por uma parcela proporcional, zerado pela ação integral, e acelarado pela ação derivativa.
Assim fica fácil né, só pode ser o mais brabo de todos, o PID.
Passo 2
II. Este controle normalmente é empregado em processos que podem admitir certa oscilação contínua da variável de controle em torno do valor desejado. São exemplos de instrumentos utilizados neste tipo de controle os pressostatos, termostatos e chaves de nível.
No item II temos um contralador que não estabiliza a variável controlada, mas que faz com que ela aoscile em torno do valor de referência.
O controlador que tem esse tipo de ação é o On/Off.
Passo 3
III. Este controle elimina o erro de forma automática gerando uma resposta transitória adequada pela ação proporcional.
A ação responsável por eliminar o erro é a ação integral e nesse caso também temos uma parcela proporcional.
Sendo assim, o controlador do item III é o PI.
Passo 4
IV. Este tipo de controle fornece uma saída proporcional ao erro permitindo o ajuste do ganho ou da banda proporcional pelo operador, de modo que o erro possa ser compensado.
Neste caso não temos nenhuma ação integrativa para anular o erro ou derivativa para acelerar a resposta, entretanto a ação proporcional que minimiza o erro ainda existe.
Logo, este é o controlador P.
Passo 5
V. Este tipo de controle, na prática, não pode ser utilizado isoladamente, porém, ao ser utilizado com outro tipo de controle, melhora a estabilidade do sistema.
O controlador que não pode ser usao sozinho mas que melhora a estabilidade do sistema é o PD. Na prática essa controlador não é estável, entretando quando se adiciona a parcela derivativa em outros controladores, ela minimiza as oscilações e torna o sistema mais rápido.
Resposta
- PID, On/Off, PI, P, PD.
Exercício Resolvido #2
Elaboração própria
Marque a alternativa correta:
a) A resposta da ação de controle P diminui o overshoot.
b) A resposta da ação de controle D elimina o erro no regime estacionário.
c) Em um controle PID, a ação de controle D acelera a resposta.
d) Em um controle PID, a ação de controle D aumenta as oscilações, bem como o tempo de resposta.
Passo 1
A primeira afirmativa diz que a ação proporcional diminui o overshoot.
Essa afirmativa está errada, uma vez que o aumento do ganho proporcional causa o aumento do overshoot pois deixa o sistema mais instável e mais oscilatório.
Passo 2
A segunda afirmativa diz que a ação deirvativa diminui o erro no regime estacionário.
Essa afirmativa também está errada, a ação derivativa não causa nenhum impacto sobre o erro em regime estacionário. Quem elimina esse erro é a ação integral.
Passo 3
Já a terceira afirmativa diz que a ação de controle derivativa é responsável por acelerar a resposta.
Essa afirmativa é portanto verdadeira uma vez que a principal função da ação derivativa é justamente aumentar a estabilidade do sistema e fazer com que sua resposta seja mais rápida.
Passo 4
A última afirmativa contradiz a terceira. Ela diz que a ação derivativa aumenta as oscilações e o tempo de resposta.
Isso está errado, como já foi explicado no passo anterior.
Resposta
c) Em um controle PID, a ação de controle D acelera a resposta.
Exercício Resolvido #3
Transpetro - 2011
Um processo submetido a controle proporcional apresenta offset para degraus no setpoint e na carga. Sabendo-se que a variável controlada não apresenta ruído de medida, adiciona-se a esse controlador o modo derivativo. Em consequência da ação derivativa, o offset:
- Não sofrerá qualquer efeito.
- Será reduzido, mas não eliminado.
- Será eliminado.
- Aumentará na forma de um degrau.
- Aumentará na forma de uma rampa.
Passo 1
Nessa questão temos um processo que está sendo controlado por um controlador proporcional.
O enunciado nos diz que para variações degrau tanto no setpoint quanto no distúrbio, o processo apresenta offset, isto é, apresenta erro no estado estacionário. Isso faz bastante sentido já que o controlador proporcional por si só não é capaz de eliminar o offset.
Sendo assim, adiciona-se ao controlado proporcional, uma parcela derivativa. E o que devemos responder é o qual o efeito dessa parcela derivativa sobre o offset.
Mas, a parcela derivativa é responsável por prever a resposta do sistema e dessa forma adiantar o controle. Ela é responsável então por acelerar a resposta e diminuir a instabilidade do sistema. Sendo assim, a ação derivativa não influencia em nada no erro em estado estacionário, portanto o item correto é o item a).
Resposta
- Não sofrerá qualquer efeito.
Exercício Resolvido #4
Fernando Mariano Bayer, Olinto César Bassi de Araújo - Controle Automático de processos – e-Tec Brasil – Santa Maria, RS, 2011 – Exercício 1 – Pág. 56.
Qual o efeito de cada modo do controlador PID sobre o offset em regime permanente para a entrada degrau?
Passo 1
A ação proporcional interfere sim no erro em estado estacionário.
Quanto maior o , menor será o offset, entratanto, mais instável será o sistema.
Apesar de o aumento do ganho do controlador proporcional diminuir o offset, esse erro nunca será nulo, portanto:
Passo 2
A ação integral, por sua vez, está diretamente relacionada ao offset. Isso porque a principal função dessa ação é justamente anular completamente o erro de estado estacionário.
Isso acontece devido ao polo na origem da função de transferência do controlador. Esse polo na origem eleva o tipo do sistema em uma unidade. Portanto se um sistema era do tipo 0, quando adiciona-se uma ação integral ele passa a ser do tipo 1, e um sistema do tipo 1 sempre apresenta erro em regime permanente igual a 0 para uma entrada degrau.
Passo 3
A ação derivativa por sua vez não impacta em nada no offset.
Sua função é antecipar a resposta do sistema tornando-o mais ágil e mais estável. Sendo assim, essa ação não tem nenhum efeito sobre o erro em regime permanente.
Resposta
Exercício Resolvido #5
2019 – Aeronáutica – FAB – CIAAR – Primeiro Tenente – Engenahria Eletrônica – Prova: 62361
Os sistemas de controle em malha fechada possuem três formas básicas de atuação que podem e são empregadas de forma combinada em função das carcaterísticas do controle desejado em cada caso particular.
Associe as colunas relacionando a forma de atuação básica de controle com suas respectivas características.
Formas de atuação básica de controle
(P) Proporcional
(I) Integrativo
(D) Derivativo
Características
( ) Produz correção significativa antes do valor do erro tornar-se grande.
( ) Atua na proporção da diferença entre o ponto de ajuste e a variável de processo.
( ) Leva o erro de estado estacionário para zero após tempo suficientemente longo.
( ) Produz um erro de estado estacionário de alguma intensidade.
( ) Responde em função do comportamento histórico recém passado do erro.
( ) Antecipa o erro atuante colaborando para aumentar a estabilidade do sistema.
A sequência correta dessa associação é:
- (P); (P); (I); (D); (I); (D).
- (D); (P); (I); (P); (I); (D).
- (D); (I); (D); (P); (P); (I).
- (P); (I); (P); (D); (I); (P).
Passo 1
Vamo lá desvendar esse enigma? Vamos indo afirmativa por afirmativa então.
( ) Produz correção significativa antes do valor do erro tornar-se grande.
A palavra chave nessa afirmativa é “antes”. A ação de controle que tem o poder de prever o erro e corrigí-lo antes mesmo de acontecer é a ação derivativa.
Então:
(D) Produz correção significativa antes do valor do erro tornar-se grande.
Passo 2
( ) Atua na proporção da diferença entre o ponto de ajuste e a variável de processo.
Essa é mole né? A ação de controle que atua na proporção do erro é a ação proporcional.
(D) Produz correção significativa antes do valor do erro tornar-se grande.
(P) Atua na proporção da diferença entre o ponto de ajuste e a variável de processo.
Passo 3
( ) Leva o erro de estado estacionário para zero após tempo suficientemente longo.
É importante que você se lembre que a única ação de controle que consegue anular o erro de estado estacionário é a ação integral.
(D) Produz correção significativa antes do valor do erro tornar-se grande.
(P) Atua na proporção da diferença entre o ponto de ajuste e a variável de processo.
(I) Leva o erro de estado estacionário para zero após tempo suficientemente longo.
Passo 4
( ) Produz um erro de estado estacionário de alguma intensidade.
Acabamos de falar que a ação integral levo o erro de estado estacionário a zero. A ação derivativa não influencia em nada no erro de estado estacionário. Portanto a ação que sempre deixa um offset é ação proporcional. Lembrando que esse erro de estado estacionário pode ser diminuído, porém nunca eliminado completamente.
(D) Produz correção significativa antes do valor do erro tornar-se grande.
(P) Atua na proporção da diferença entre o ponto de ajuste e a variável de processo.
(I) Leva o erro de estado estacionário para zero após tempo suficientemente longo.
(P) Produz um erro de estado estacionário de alguma intensidade.
Passo 5
( )Responde em função do comportamento histórico recém passado do erro.
A ação que responde em função do histórico é a ação integral. Lembre sempre: a ação derivativa antecipa o erro e a ação integral corrige os erros passados.
(D) Produz correção significativa antes do valor do erro tornar-se grande.
(P) Atua na proporção da diferença entre o ponto de ajuste e a variável de processo.
(I) Leva o erro de estado estacionário para zero após tempo suficientemente longo.
(P) Produz um erro de estado estacionário de alguma intensidade.
(I)Responde em função do comportamento histórico recém passado do erro.
Passo 6
( ) Antecipa o erro atuante colaborando para aumentar a estabilidade do sistema.
Novamente uma afirmativa falando em correção antecipatória, logo, sabemos se tratar da ação derivativa
(D) Produz correção significativa antes do valor do erro tornar-se grande.
(P) Atua na proporção da diferença entre o ponto de ajuste e a variável de processo.
(I) Leva o erro de estado estacionário para zero após tempo suficientemente longo.
(P) Produz um erro de estado estacionário de alguma intensidade.
(I)Responde em função do comportamento histórico recém passado do erro.
(D) Antecipa o erro atuante colaborando para aumentar a estabilidade do sistema.
Resposta
- (D); (P); (I); (P); (I); (D).
Exercício Resolvido #6
2015 - CIAAR - Engenahria Eletrônica – Prova: 52825
Controladores PID são muito comuns em processos produtivos na indústria. Sobre sistemas de controle PID, assinale a alternativa incorreta.
- Um aumento excessivo da ação integral em um controlador tornará o sistema mais estável.
- A ação derivativa possui como função melhorar o comportamento transitório do sistema em malha fechada.
- O aumento do ganho proporcional de um controlador atua diretamente na velocidade de resposta do sistema.
- O limiar de estabilidade de um controlador proporcional ocorre quando o sistema apresenta oscilação sustentada.
Passo 1
a) Um aumento excessivo da ação integral em um controlador tornará o sistema mais estável.
Essa afirmativa está incorreta uma vez que a ação integral apesar de levar a zero o erro de regime permanente, também causa instabilidade no sistema. Dessa forma, um aumento na ação integral causa o aumento da instabilidade do sistema.
Passo 2
b) A ação derivativa possui como função melhorar o comportamento transitório do sistema em malha fechada.
Essa afirmativa é correta. Como a ação derivtiva tem a capacidade de antecipar a resposta do sistema, ela torna a resposta mais rápida e mais instável, diminuindo as oscilçaõe e o overshoot.
Passo 3
c) O aumento do ganho proporcional de um controlador atua diretamente na velocidade da resposta do sistema.
Essa afirmativa é correta. Quando se aumenta o ganho proporcional de um sistema, o erro em regime permanente é reduzido, entretanto, o sistema torna-se mais instável e consequentemente mais lento.
Passo 4
d) O limiar de estabilidade de um controlador proporcional ocorre quando o sistema apresenta oscilações sustentadas.
Essa afirmativa também está correta. Quando o sistema apresenta oscilações sustentadas ele está no limite de sua estabilidade, qualquer mínima mudança como um pequeno acréscimo no ganho proporcional pode troná-lo instável com oscilações crescentes.
Resposta
a) Um aumento excessivo da ação integral em um controlador tornará o sistema mais estável.
Exercício Resolvido #7
2015 - CESGRANRIO – Petrobrás – Técnico de Manuntenção Junior – Instrumentação – 2012 – Prova: 10453
Um sistema de controle realimentado por um controlador PID apresenta um percentual de ultrapassagem (overshoot) de para uma entrada degrau.
Qual mudança deve ser na sintonia desse controlador para reduzir esse percentual?
- Reduzir os ganhos proporcional e integral e aumentar o ganho derivativo.
- Reduzir o ganho derivativo, mantendo os valores dos ganhos proporcional e integral.
- Aumentar o ganho integral e manter os valores dos ganhos proporcional e derivativo.
- Aumentar os ganhos proporcional e integral e manter o valor do ganho derivativo.
- Aumentar o ganho proporcional, mantendo os valores dos ganhos derivativo e integral.
Passo 1
O overshoot é causado pela oscilação da resposta. Quanto mais instável for um sistema mais ele oscilará.
Portanto, para reduzir o overshoot precisamos procurar por soluções que atuem na estabilidade do sistema.
A ação proporcional e integral são ações que quanto maior seus efeitos, maior é a instabilidade do sistema, então precisamos diminuir seus ganhos.
Já a ação derivativa é o oposto, sua função é justamente tornar o sistema mais estáel e menos oscilatório, sendo assim, precisamo aumentar seu ganho.
Portanto, a alternativa correta é a alternativa a).
Resposta
a) Reduzir os ganhos proporcional e integral e aumentar o ganho derivativo.
Exercício Resolvido #8
PETROBRAS (2012)
O gráfico acima mostra comparativamente alguns modos de controle aplicados em ajuste de controladores de processo. Os modos de controle descritos em X, Y e Z são respectivamente:
- Proporcional; Proporcional + integral; proporcional + integral + derivativo.
- Proporcional + derivativo; proporcional + integral + derivativo; proporcional.
- Proporcional + derivativo; Proporcional + integral; proporcional.
- Proporcional + integral + derivativo; proporcional + derivativo; proporcional.
- Proporcional + integral + derivativo; proporcional + integral; proporcional.
Passo 1
Vamos analisar os gráficos apresentadas e ver quais conclusões podemos tirar de cada um deles.
Começando pela curva Z que é a mais diferente das três.
Podemos perceber que a curva Z não estabiliza no ponto de referência, o que nos mostra que ela deixa erro no estado permanente e portanto não possui ação integral.
Como controladores PD são muito instáveis e na prática não são usados, a curva Z só pode representar um controlador proporcional.
Passo 2
Vamos ver agora as curvas X e Y.
As duas são bem parecidas, ambas não apresentam offset o que nos diz que possuem ação integral.
Entretanto a curva X oscila menos e é mais rápida que a curva Y o que indica que a curva X possui uma ação derivativa enquanto a Y não possui.
Sendo assim, X representa um controlador PID, enquanto Y é um controlador PI.
Resposta
e) Proporcional + integral + derivativo; proporcional + integral; proporcional.