Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Lugar geométrico das raízes

Ver Todos os Exercícios

Teoria

Introdução

Agora que já aprendemos um pouco sobre estabilidade e quais critérios usar para determinar se um sistema é estável ou não, vamos aprender uma técnica muito importante em controle de processos que nos permite analisar o efeito do ganho da malha sobre a sua resposta e estabilidade.

Imagina que a gente esteja projetando uma malha de controle para um circuito elétrico conforme o diagrama de blocos abaixo. Nós queremos variar o ganho dessa malha, mas não sabemos o quanto poderemos mexer nesse ganho sem que a malha fique instável.

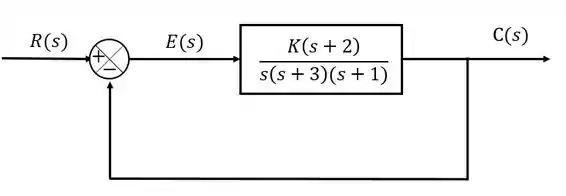
Nesse caso, a nossa função de transferência será:

C s R s = K s + 2 s s + 3 ( s + 1 ) 1 + K s + 2 s s + 3 ( s + 1 )

Rearranjando:

C s R s = K ( s + 2 ) s s + 3 s + 1 + K ( s + 2 )

Então, a nossa equação característica vai ser:

s s + 3 s + 1 + K s + 2 = 0

Perceba que ela está em função de K , e que dependendo do valor de K , os valores das raízes serão alterados. Como a estabilidade do sistema depende que as raízes da equação característica sejam negativas, a estabilidade do sistema será completamente dependente do valor de K .

O lugar das raízes é uma técnica que nos permite determinar o lugar das raízes no plano quando variamos o valor do K . Nessa técnica nós pegaremos a função de transferência em malha aberta e seguindo algumas regrinhas, poderemos determinar como se comportam as raízes do sistema em malha fechada para diferentes valores de K .

Os primeiros passos

Vamos então estabelecer algumas regras para conseguirmos esboçar nosso diagrama de lugar das raízes.

Vamos continuar trabalhando com a função de transferência que estávamos vendo ali em cima. A função de transferência em malha aberta do sistema é:

G s = K s + 2 s s + 3 ( s + 1 )

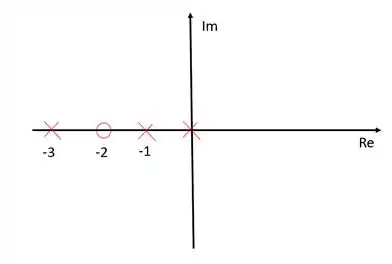
Precisamos definir algumas coisas. As raízes do polinômio do numerador são chamadas de zeros, enquanto as raízes do polinômio do denominador são chamadas de polos. Portanto esse sistema tem um zero em malha aberta, - 2 , e três polos em malha aberta, 0 , - 3 e - 1 .

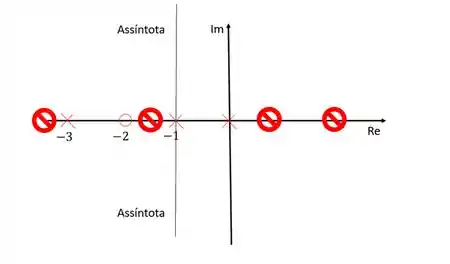
Para fazer o esboço o lugar das raízes em malha fechada do sistema, nós usaremos os polos e zero em malha aberta. Para esboçar o diagrama de lugar das raízes, a primeira coisa sempre será marcar os zeros e polos da função de transferência em malha aberta. Vamos representar os zeros com um círculo e os polos com um xis.

As assíntotas

O próximo passo será desenhar nossas assíntotas. As assíntotas são importantes porque na maioria dos casos, o nosso lugar das raízes terá pelo menos um ramo tendendo ao infinito. As assíntotas serão a bússola que vai nos mostrar para onde os nossos ramos deverão convergir no infinito. O número de polos a mais que zeros sempre nos indicará o número de assíntotas que precisaremos calcular.

Para traçar essas assíntotas, nós usaremos uma fórmula para saber onde elas interceptam o eixo dos reais:

σ a = ∑ p o l o   f i n i t o s - ∑ z e r o s   f i n i t o s n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s

E também temos uma fórmula para determinar o ângulo que essa interceptação acontece:

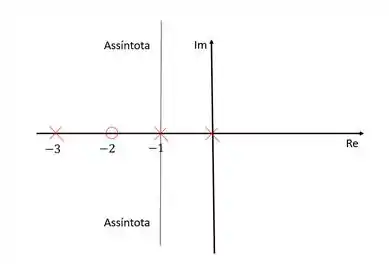
θ a = ± 180 2 r + 1 n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s

Vamos calcular para o nosso exemplo:

σ a = - 3 + 0 + ( - 1 ) - - 2 3 - 1 = - 1

θ a = ± 180 2 r - 1 3 - 1 = ± 90 ( 2 r - 1 )

r = 0,1 ,   2 ,   3 … .

Se r for igual a 0 , o ângulo será 90 º , se r for igual a 1 , o ângulo será 270 º (ou - 90 º ). A partir daí os resultados se repetem. Como precisamos de dois zeros no infinito, duas assíntotas são suficientes. E pela primeira fórmula, calculamos que essas assíntotas interceptam o eixo dos reais em - 1 .

Desenhando as assíntotas no diagrama:

As regrinhas

Com as assíntotas traçadas, só nos resta traçar o lugar das raízes de fato. Os ramos do lugar das raízes mostra para nós onde as raízes do sistema em malha fechada estarão caso o ganho varie. No começo de cada ramo teremos as raízes caso K = 0 , enquanto no final de cada ramos teremos as raízes caso K → ∞ . Ou seja, cada ramo representa o comportamento de uma raiz conforme K vai de 0 a ∞ .

Para desenhar os ramos, devemos sempre seguir as regrinhas abaixo:

  • O número de ramos é igual ao número de polos, isso acontece porque o número de raízes de um sistema em malha fechada sempre será igual ao número de polos em malha aberta do sistema;
  • O diagrama sempre será simétrico com relação ao eixo real;
  • Os ramos sempre estarão à esquerda de um número ímpar de polos e zeros sobre o eixo dos reais; Ou seja, para o nosso sistema, não podem existir ramos nos lugares marcados:

  • Os ramos sempre começam nos polos e terminam nos zeros;
  • As funções podem ter zero no infinito, eles são sempre indicados pelas assíntotas que já calculamos. Para o nosso exemplo nós temos um zero finito e dois zeros no infinito, totalizando três zero, o que faz sentido, já que teremos três ramos que deverão sair dos polos e morrer nos zeros

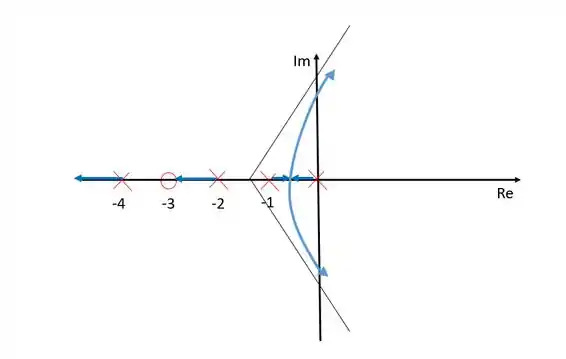
Vamos esboçar isso então:

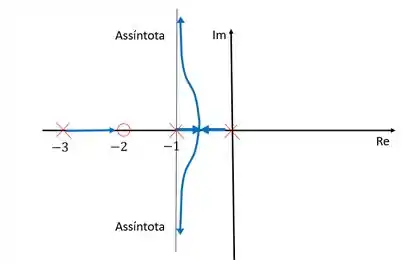
Vamos analisar o que a gente fez.

Primeiramente devemos ter em mente que os únicos trechos sobre o eixo dos reais que pode existir ramos é entre - 3 e - 2 , e entre - 1 e 0 , pois esses trechos estão à esquerda de uma quantidade ímpar de polos e zeros. É por isso que o ramo que nasce em - 3 morre em - 2 e não o que nasce - 1 .

Entre - 1 e 0 existe um trecho onde pode existir ramos. Como esse intervalo está delimitado por dois polos, os ramos nascem nesses polos e se encontram no meio do intervalo. Quando eles se encontram eles precisam morrer em um zero, e por isso tendem assintoticamente aos zeros no infinito determinados pelas assíntotas.

Por fim, podemos ver pelo diagrama que a regra de simetria com relação ao eixo dos reais foi obedecida. Ou seja, tudo certinho.

Um detalhe importante: as assíntotas não fazem parte do diagrama do lugar das raízes, elas simplesmente indicam em que lugar estarão os zeros no infinito. As raízes estão sempre localizadas sobre os ramos que estão representados por setas azuis.

A principal análise que podemos fazer com esse exemplo é que o sistema é estável não importa qual seja o valor de K , uma vez que os ramos que representam as raízes do sistema em malha fechada nunca atravessam o eixo dos números imaginários e ficam sempre no semiplano esquerdo do diagrama. Como as raízes são sempre negativas para qualquer valor de K , a estabilidade desse sistema não depende do ganho.

Propriedade do lugar das raízes

O lugar das raízes tem duas propriedades muito importantes. Vamos considerar a função de transferência em malha fechada genérica abaixo.

C s R s = K G s 1 + K G s

Essa é a função de transferência de um sistema feedback normal, porém ela está em função de K . A equação característica é o denominador dessa função:

1 + K G s = 0

K G s = - 1

Agora iremos aplicar uma propriedade que será muito importante para nós em lugar das raízes e mais futuramente em resposta em frequência que se chama ângulo de fase. O ângulo de fase é o ângulo que o número complexo forma no plano com o eixo dos reias.

∠ K G s = ∠ - 1

Como - 1 é um número real puro negativo, seu ângulo de fase é 180 º .

Entretanto, como os ângulos se repetem a cada 360 º , o ângulo de fase de - 1 acaba sendo todos os múltiplos ímpares de 180 º .

∠ K G s = 180 ° ( 2 r + 1 )

r = 0,1 , 2,3 …

Essa propriedade nos diz que dado um certo ponto qualquer no lugar das raízes a soma dos ângulos de todos os zeros e polos da função de transferência em malha aberta tem que ser igual a um múltiplo ímpar de 180 ° . Sendo que os zeros contribuem positivamente para a soma enquanto os polos contribuem negativamente.

Sendo assim, para o nosso exemplo, se a gente pegar qualquer ponto aleatório como eu fiz abaixo, teremos:

θ 3 - θ 1 - θ 2 - θ 4 = 180 ° ( 2 r + 1 )

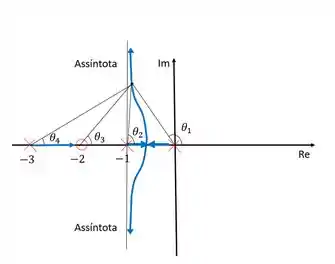
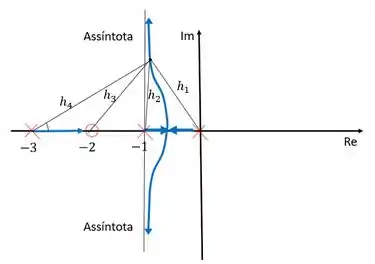
Além disso, outra propriedade do lugar das raízes é que o ganho do sistema em qualquer ponto é igual ao módulo do inverso das funções de transferência:

K = 1 G s H s

Esse módulo pode ser calculado como a razão das distâncias dos zeros e dos polos a qualquer ponto do lugar das raízes.

K = ∏ d i s t â n c i a   d o s   p o l o s ∏ d i s t â n c i a   d o s   z e r o s  

Para o nosso exemplo:

K = h 1 h 2 h 4 h 3

Os primeiros passos

As assíntotas

As regrinhas

Propriedade do lugar das raízes

Exercícios Resolvidos

Exercício Resolvido #1

Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 254, Problema 8-1b

Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:

G s = K ( 3 s + 1 ) ( 2 s + 1 )

Passo 1

Essa função de transferência apresenta um zero, - 1 3 , e um polo, - 1 2 . Vamos começar representando eles em nosso diagrama:

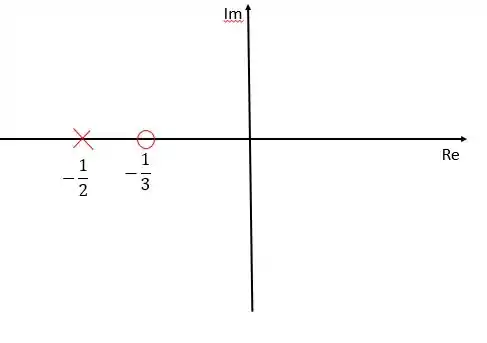
Passo 2

Essa função de transferência tem o mesmo número de polo e de zeros, ou seja, não existe nenhum zero no infinito, e portanto, não precisamos calulcar as assíntotas para determinar esse zero.

Sendo assim, já podemos representar nossos ramos. Lembrando sempre de observar todas as regrinhas.

O número de ramos é igual ao número de polos, nesse caso então, só teremos um ramo.

Só pode existir um ramo se à esquerda dele existir um número ímpar de polos e zeros. Ou seja, à direita de - 1 3 não existe ramo pois nesse intervalo não existe nenhum zero ou polo à esquerda e à esquerda de - 1 2 também não pode ter ramo porque nesse intervalo existe um zero e um polo à esquerda, dando um total de dois que é um núemero par.

Outra regra importante é que todo ramos nasce em um polo e morre em um zero. Como só temos um polo e um zero, nosso diagrama ficará da seguinte forma:

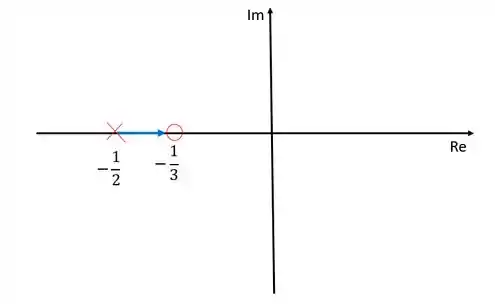
Repare que dessa forma, todas as regras foram obedecidas.

Resposta

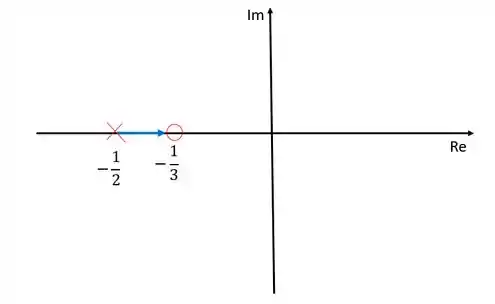
Exercício Resolvido #2

Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 254, Exemplo 8-2.1. Adaptado

Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:

G s = K C ( 3 s + 1 ) ( s + 1 )

Passo 1

Como sempre, a primeira coisa que devemos começar fazendo é identificar quantos e quais são os polos e zeros da função de transferência.

Para este caso, nós não temos nenhum zero na função de transferência, porém temos dois polos, - 1 3 e - 1 . Vamos marcar eles no diagrama então:

Passo 2

Como temos dois polos a mais que zeros, isso indica que teremos dois zeros no infinito no nosso diagrama. Para saber a localização desses zeros desenharemos assíntotas no diagarama de lugar das raízes que vão nos indicar onde eles se encontram.

θ a = ± 180 2 r + 1 n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s =   ± 180 2 r + 1 2 - 0 = 9 0 ( 2 r + 1 )

Podemos perceber que se   r for igual a 0 o ângulo será 9 0 º , se for 1 , será 27 0 º . Após isso, os valores 90 º e 180 º começam a se repetir.

Agora vamos calcular onde a assíntota intercepta o eixo real:

σ a = ∑ p o l o   f i n i t o s - ∑ z e r o s   f i n i t o s n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s = - 1 - 1 / 3 - 0 2 - 0 =   - 2 3

Coocando no diagrama de lugar das raízes:

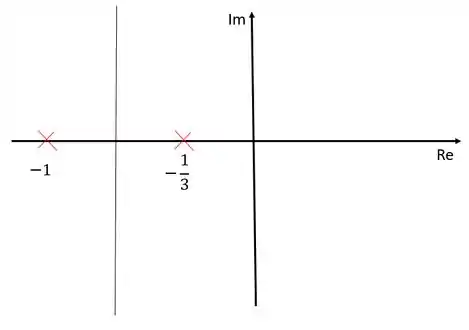
Repare que temos duas assíntotas, uma com inclinação 90 º e outra com inclinação 270 º .

Passo 3

Por fim devemos representar os ramos, eu são as linhas eu indicam o lugar das raízes conforme varíamos algum coeficiente (nesse caso, o ganho). Lembre-se sempre que o número de ramos é sempre igual ao númeor de polos e que cada ramos “nasce” em um polo e “morre” em um zero. Então nesse caso nós teremos um ramo saindo de cada um dos polos e indo até um zero no infinito pois não temos nenhum zero finito.

Outro detalhe importante é que os ramos só existem no eixo dos reais se estiverem à esquerda de um número ímpar de polos, ou seja, não pode existir nenhum ramo à direita de - 1 3 pois nesse caso não teríamos nenhum polo à esquerda, nem à esquerda de - 1 pois aí teríamos dois polos à esquerda.

Sendo assim, o nosso diagram de lugar das raízes fica da seguinte forma:

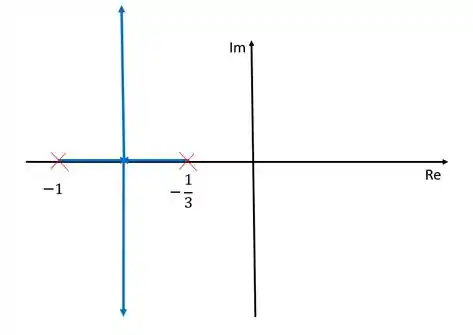
Nesse caso, coincidentemente, o ramo do lugar das raízes ficou sobre as assíntotas, mas tenha em mente que nem sempre será assim.

Resposta

Exercício Resolvido #3

Elaboração própria

Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:

G s = K ( s + 1 ) ( 0,5 s + 1 ) ( 2 s + 1 )

Passo 1

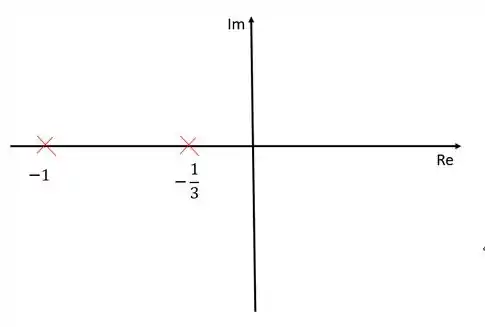
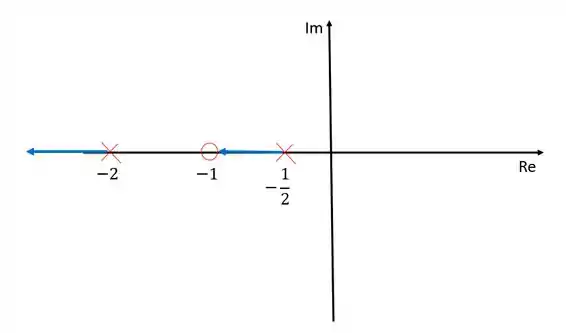
O primeiro passo sempre será identificar os polos e zeros da função de transferência. Nesse exercício temos um zero, - 1 , e dois polos, - 2 e - 1 2 .

Representando esses polos e zeros no diagrama de lugar das raízes:

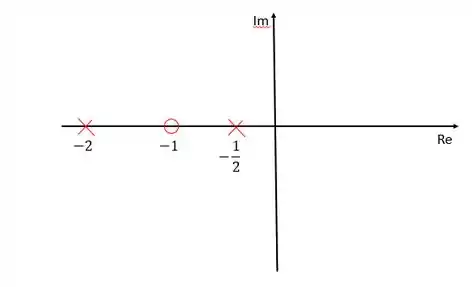
Passo 2

Como temos um polo a mais que zero, teremos um zero no infinito. Então precisamos calular nossas assíntotas para saber onde esse zero no infinito se encontra.

θ a = ± 180 2 r + 1 n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s =   ± 180 2 r + 1 2 - 1 = 180 ( 2 r + 1 )

A assíntota terá inclinação 180 º não importa qual seja o valor de r .

Como a inclinação da assíntota é de 180 º , ela está sobre todo o eixo dos reais, então não é preciso calcular onde essa asspintota intercepta o eixo.

Passo 3

Só precisamos agora representar os ramos do lugar das raízes seguindo todas aquelas regrinhas. Os ramos nascem nos polos e morrem nos zeros. O número de ramos é igual ao número de polos, e os ramos só existem se à esquerda deles existir um número ímpar de polos e zeros.

Portanto:

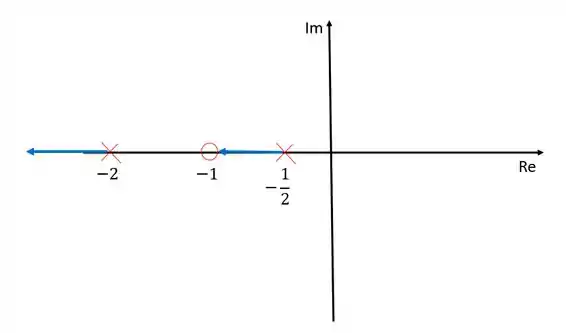
O ramo que sai do polo - 2 é o ramo que morre no zero no infinito que se encontra sobre o eixo dos reais, já que a assíntota tem inclinação 180 º .

Entre - 1 e - 1 2 não pode existir ramos pois existe um número par de ramos e zeros à esquerda desse intervalo.

Resposta

Exercício Resolvido #4

Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 8.3

Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:

G s = K ( s + 2 ) ( s + 4 ) ( s + 6 )

Passo 1

O primeiro passo para montar o nosso esboço do lugar das raízes sempre será identidicar os polos e zeros da nossa função de transferência e representa-los no diagrama.

A função de transferência do exercício não apresenta zeros porém possui três polos, - 2 , - 4 e - 6 .

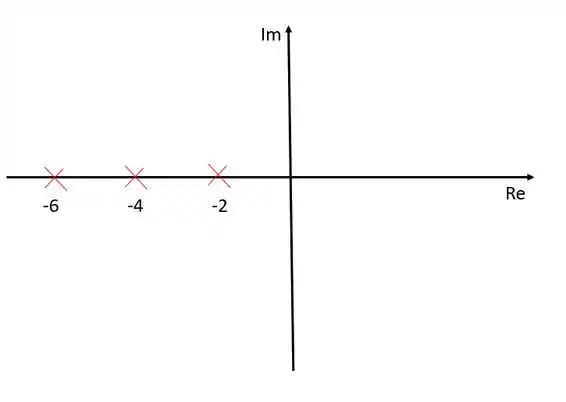
Passo 2

Agora, vamos aplicar as nossas fórmulas para encontrar o ângulo das assíntotas com o eixo dos reais e em que ponta elas vão interceptar esse eixo:

θ a = ± 180 2 r + 1 n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s =   ± 180 2 r + 1 3 - 0 = 60 ( 2 r + 1 )

Podemos perceber que se   r for igual a 0 o ângulo será 60 º , se for 1 , será 180 º , e se for 2 será 300 º . Repare que se continuarmos aumentando o valor de r esses valores vão se repetir.

Agora vamos calcular onde a assíntota intercepta o eixo real:

σ a = ∑ p o l o   f i n i t o s - ∑ z e r o s   f i n i t o s n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s = - 2 - 4 - 6 - 0 3 - 0 =   - 4

Coocando no diagrama de lugar das raízes:

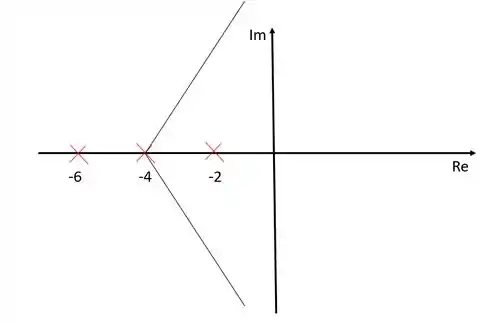
Estão representadas as assíntotas com inclinação 60 º e 300 º . A assíntota com inclinação 180 º está localizada sobre o eixo dos reais.

Passo 3

Agora devemos começar a representar os ramos. Os ramos sempre começam nos polos e terminam nos zeros. Como nesse caso não temos zeros finitos, nós precisaremos que os polos terminem nos zeros no infinitos, ou seja, precisaremos de três zeros no infinito.

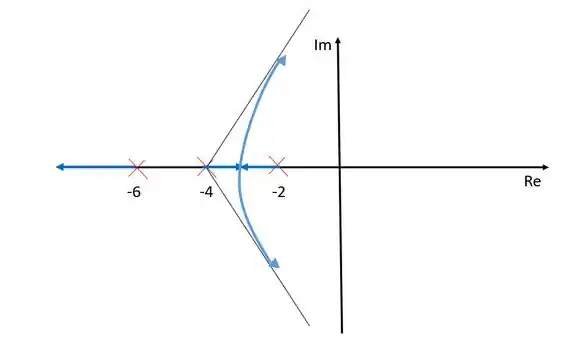
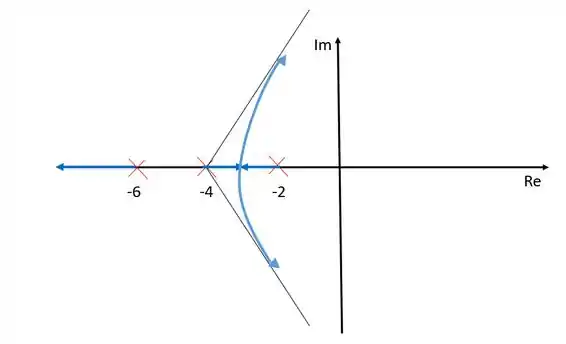
Entre 0 e - 2 e entre - 4 e - 6 não podem existir ramos sobre o eixo real pois nesses lugares estão à esquerda de um número par de zeros e polos. Dessa forma ficamos com um ramo saindo do polo - 6 e vai para o infinito negativo real, e outros dois ramos saindo de - 2 e - 4 que se encontram deixam o eixo dos reais tendendo aos zeros no infinito indicados pelas assíntotas.

Resposta

Exercício Resolvido #5

Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 254, Exemplo 8-2.2. Adaptado

Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:

G s = K C ( 3 s + 1 ) ( s + 1 ) ( 0,5 s + 1 )

Passo 1

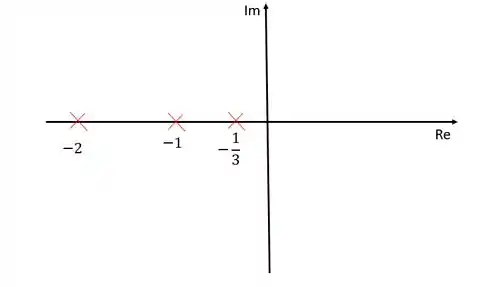
Primeiramente vamos identificar nosso polos e zeros. Nesse caso, temos três polos, - 1 3 , - 1 e - 2 , e nenhum zero.

Representando esses polos no diagrama de lugar das raízes:

Passo 2

Nesse caso, temos três polos a mais que zeros, isso indica que teremos três zeros no infinito, e portanto, precisamos das nossas assíntotas para saber a localização desses polos.

θ a = ± 180 2 r + 1 n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s =   ± 180 2 r + 1 3 - 0 = 60 ( 2 r + 1 )

Podemos perceber que se   r for igual a 0 o ângulo será 60 º , se for 1 , será 180 º , e será 300 º se r for 3 . Após isso, os valores começam a se repetir.

Agora vamos calcular onde a assíntota intercepta o eixo real:

σ a = ∑ p o l o   f i n i t o s - ∑ z e r o s   f i n i t o s n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s = - 1 - 1 3 - 2 - 0 3 - 0 =   - 10 9

Colocando no diagrama de lugar das raízes:

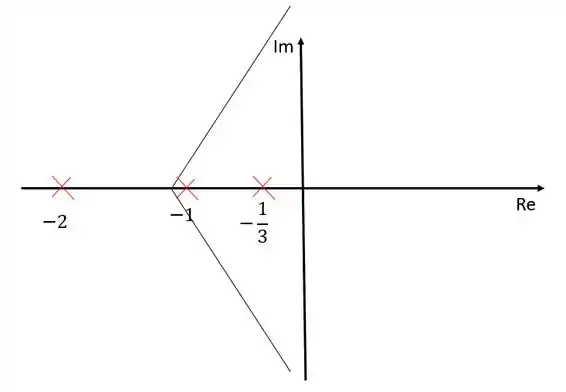
Temos uma assíntota com inclinação 60 º , uma assíntota com inclinação 300 º e uma terceira assíntota com inclinação 180 º que se encontra sobre o eixo dos reais.

Passo 3

Agora só nos resta representar os ramos, lembrando sempre das nossas regrinhas: os ramos nascem nos polos e morrem nos zeros, o número de ramos é igual ao número de polos, e os ramos só existem se à esquerda deles existir um número ímpar de polos e zeros.

Se observarmos todas essas regras, nosso diagram ficará dessa forma:

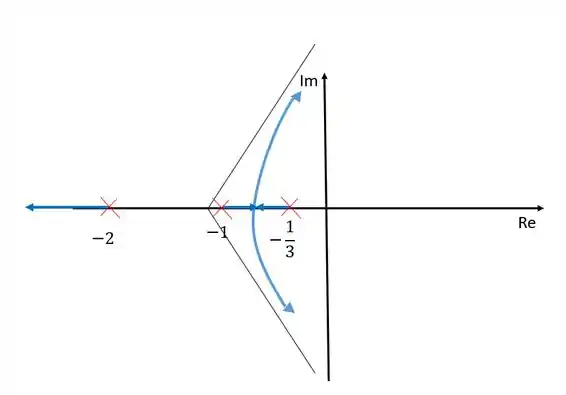
Cada ramo nasce em um polo e morre em um zero no infinito, já que não temos nenhum zero finito nesse caso. Os zeros no infinito são determinados pelas assíntotas e portanto os ramos tendem à eles.

Entre - 1 e - 2 não existem ramos porque nesse intervalo existem dois polos à esquerda.

Resposta

Exercício Resolvido #6

Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 254, Exemplo 8-2.2. Adaptado

Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:

G s = K C ( 3 s + 1 ) ( s + 1 ) ( 0,5 s + 1 )

Passo 1

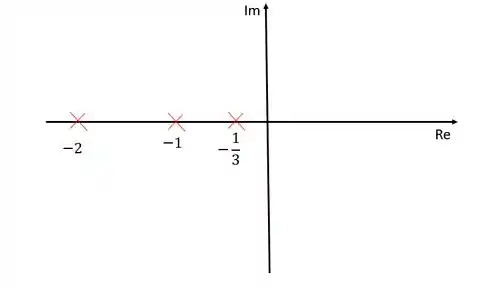
Primeiramente vamos identificar nosso polos e zeros. Nesse caso, temos três polos, - 1 3 , - 1 e - 2 , e nenhum zero.

Representando esses polos no diagrama de lugar das raízes:

Passo 2

Nesse caso, temos três polos a mias que zero, isso indica que termos três zeros no infinito, e poranto, precisamos das nossas assíntotas para saber a localização desses polos.

θ a = ± 180 2 r + 1 n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s =   ± 180 2 r + 1 3 - 0 = 60 ( 2 r + 1 )

Podemos perceber que se   r for igual a 0 o ângulo será 60 º , se for 1 , será 180 º , e será 300 º se r for 3 . Após isso, os valores começam a se repetir.

Agora vamos calcular onde a assíntota intercepta o eixo real:

σ a = ∑ p o l o   f i n i t o s - ∑ z e r o s   f i n i t o s n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s = - 1 - 1 3 - 2 - 0 3 - 0 =   - 10 9

Coocando no diagrama de lugar das raízes:

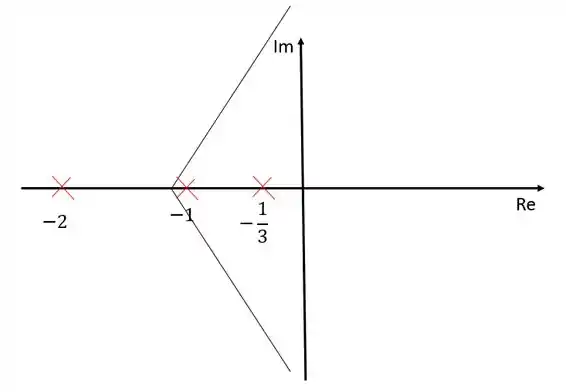
Temos uma assíntota com inclinação 60 º , uma assíntoa com inclinação 300 º e uma terceira assíntota com inclinação 180 º que se encontra sobre o eixo dos reais.

Passo 3

Agora só nos resta representar os ramos, lembrando sempre das nossas regrinhas: os ramos nascem nos polos e morrem nos zeros, o número de ramos é igual ao número de polos, e os ramos só existem se à esquerda deles existir um número ímpar de polos e zeros.

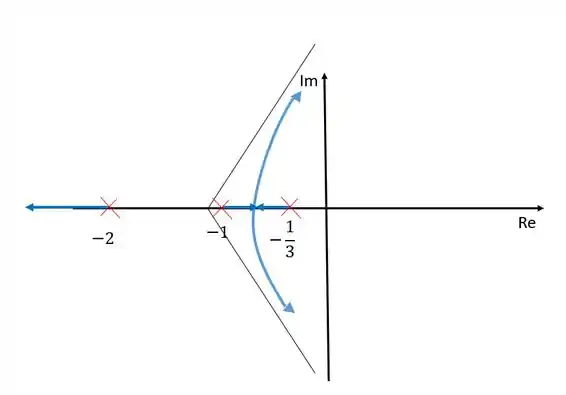
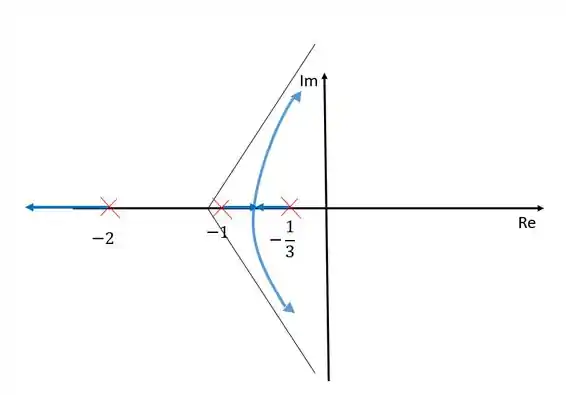
Se observarmos todas essas regras, nosso diagram ficará dessa forma:

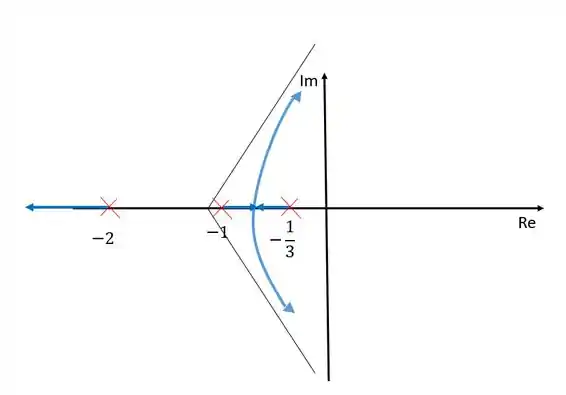
Cada ramo nasce em um polo e morre em um zero no infinito, já que não temos nenhum zero finito nesse caso. Os zeros no infinito são determinados pelas assíntotas e portanto os remaos tendem à eles.

Entre - 1 e - 2 não existem ramos porque nesse intervalo existem dois polos à esquerda.

Resposta

Exercício Resolvido #7

Elaboração própria

Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:

G s = K s ( s + 1 ) ( s + 2 ) ( s + 3 )

Passo 1

Essa função de transferência apresenta um zero em 0 e três polos em - 1 , - 2 e - 3 .

Representando esses polos e zeros no diagrama de lugar das raízes:

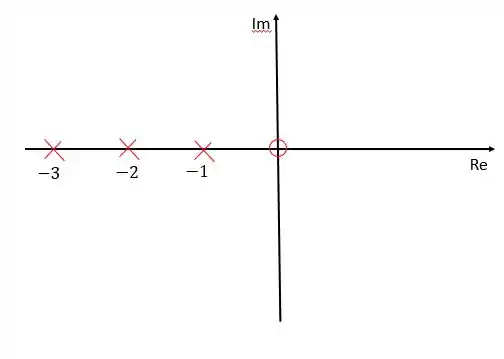
Passo 2

Nesse caso temos dois polos a mais que zeros, então teremos dois zeros no infinito. Precisamos então calcular nossas assíntotas:

θ a = ± 180 2 r + 1 n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s =   ± 180 2 r + 1 3 - 1 = 90 ( 2 r + 1 )

A assíntota terá inclinação 90 º se r for igual 0 , e 270 º se r for igual a 1. Após isso, os valores começam a se repetir.

Agora vamos calcular onde a assíntota intercepta o eixo real:

σ a = ∑ p o l o   f i n i t o s - ∑ z e r o s   f i n i t o s n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s = - 1 - 2 - 3 - 0 3 - 1 =   - 3

Coocando no diagrama de lugar das raízes:

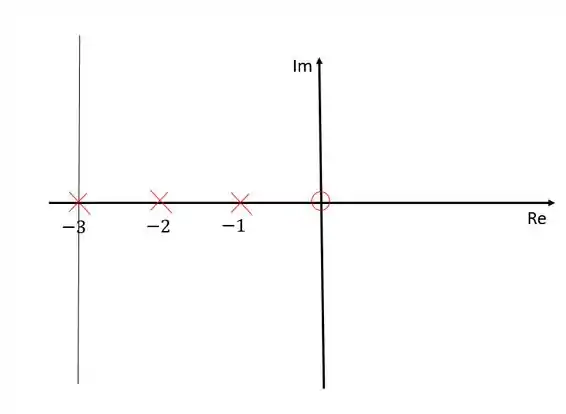
Passo 3

Só precisamos agora representar os ramos do lugar das raízes seguindo todas aquelas regrinhas. Os ramos nascem nos polos e morrem nos zeros. O número de ramos é igual ao número de polos, e os ramos só existem se à esquerda deles existir um número ímpar de polos e zeros.

Portanto:

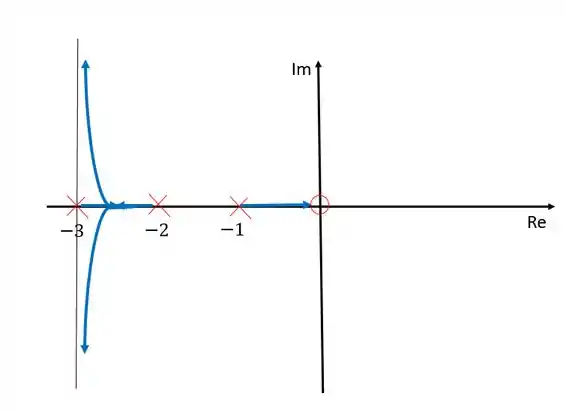
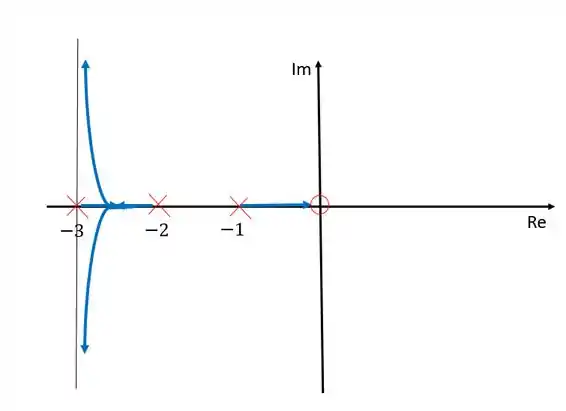
Nesse caso nós temos três ramos pois temos três polos. Entre - 2 e - 1 não pode haver nenhum ramo pois existe uma uantidade par de polos e zeros à esquerda desse trecho. Como temos dois polos a mais que zeros, dois ramos morrerão no infinito. Esses ramos saem de - 2 e - 3 , se encontram no meio desse trecho e depois tendem assintoticamente aos zeros determinados pelas assíntotas calculadas.

Resposta

Exercício Resolvido #8

Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 8.2

Esboce o lugar geométrico das raízes para o sistema mostrado abaixo:

G s = K s + 3 s s + 1 s + 2 s + 4

Passo 1

O primeiro passo para montar o nosso esboço do lugar das raízes sempre será identidicar os polos e zeros da nossa função de transferência e representa-los no diagrama.

A função de transferência do exercício apresente um zero, - 3 , e quatro polos, 0 , - 1 , - 2 e - 4 :

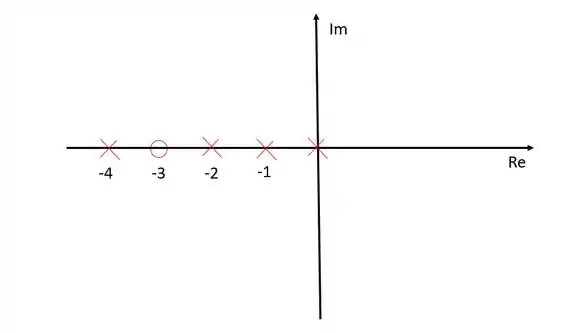
Passo 2

Agora, vamos aplicar as nossas fórmulas para encontrar o ângulo das assíntotas com o eixo dos reais e em que ponta elas vão interceptar esse eixo:

θ a = ± 180 2 r + 1 n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s =   ± 180 2 r + 1 4 - 1 = 60 ( 2 r + 1 )

Podemos perceber que se   r for igual a 0 o ângulo será 60 º , se for 1 , será 1 80 º , e se for 2 será 300 º . Repare que se continuarmos aumentando o valor de r esses valores vão se repetir.

Agora vamos calcular onde a assíntota intercepta o eixo real:

σ a = ∑ p o l o   f i n i t o s - ∑ z e r o s   f i n i t o s n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s = - 4 - 2 - 1 - 0 - - 3 4 - 1 =   - 4 3

Coocando no diagrama de lugar das raízes:

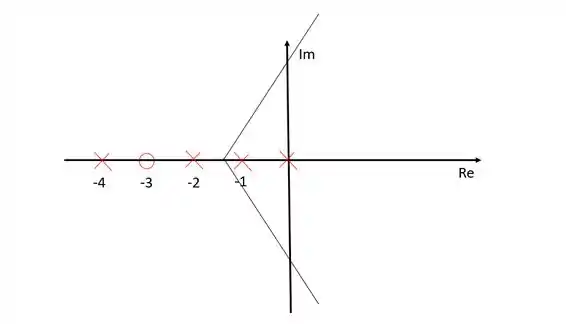
Estão representadas as assíntotas com inclinação 60 º e 300 º . A assíntota com inclinação 180 º está localizada sobre o eixo dos reais.

É importante ressaltar que as assíntotas não fazem parte do diagrama de lugar das raízes, elas apenas indicam onde estão localizados os zeros no infinito do sistema. Como nesse caso temos três polos a mais que zeros, precisaremos de três zeros no infinito.

Passo 3

Agora devemos representar de fato as linhas do lugar das raízes (os ramos). Primeiramente devemos lembrar que a quantidade de ramos é igual à quantitade do número de polos do sistema. Os ramos sempre começam em um polo e terminam em um zero e sempre estão localizados à esquerda de um número ímpar de par ou polos no eixo real. Sendo assim:

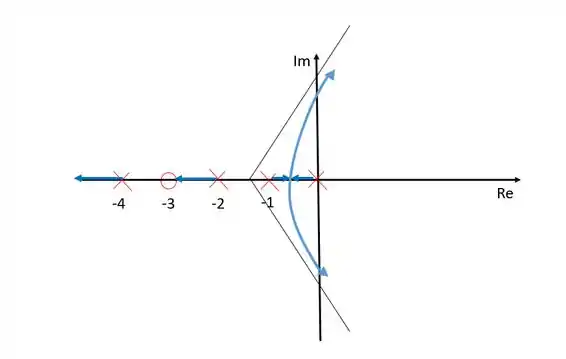
Repare que entre - - 1 e - 2 e entre - 3 e - 4 não existe nenhum ramo pois eles estão a esquerda de um número par de polos e zeros. Todos os ramos começam em polos e terminam em zeros e que existem três zeros no infinito.

Resposta