Teorema de Laplace
Teoria
Fala aí!
Vamos estudar aqui um teorema que vai nos ajudar a calcular determinantes de matrizes grandes. É bem comum usarmos esse teorema para calcularmos determinantes de matrizes ou maiores, mas ele serve até para as matrizes pequenas. Nesse caso, o teorema faz com que a gente diminua nosso trabalho. Através dele vamos precisar calcular determinantes de matrizes menores do que a nossa matriz original! Essa é a vantagem desse teorema!!
Ficou animado? Aguenta um pouquinho que eu vou te ensinar a calcular um carinha que vai ser muito importante para o teorema de Laplace. Esse cara é o chamado cofator.
Cofator
Vamos começar considerando uma matriz qualquer. Eu vou escolher uma só para simplificar a ideia. A matriz é essa daqui:
O cofator vai estar sempre associado a algum elemento da nossa matriz (um daqueles números que estão na matriz). Então vamos lá, vamos calcular o cofator de algum elemento ali, qualquer um vai... hum... vou escolher aquele 3 ali. O primeiro passo para calcular o cofator associado a este elemento é marcar a linha do elemento escolhido e a sua coluna. Dica: Se marcar sua linha e coluna dessa maneira aqui, vai te ajudar mais para frente:
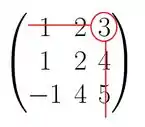
A linha do elemento 3 é a linha 1,onte temos os números 1 e 2 que a gente marcou ali, e a coluna que marcamos é a coluna 3, onde temos os números 4 e 5 que também estão marcados.
Beleza, agora podemos calular o cofator associado a este elemento.
O símbolo que representa o cofator é onde o índice representa a linha do elemento que a gente escolheu (que aqui vai ser 1) e o representa a coluna do elemento escolhido (nesse exemplo vai ser 3). No nosso exemplo, então, a gente quer calcular o cofator !
Como que a gente calcula esses carinhas? Através dessa fórmula estranha que eu já vou te explicar:
Esquista, não? Mas calma que a gente vai entender.
Começamos por aquele ali. Nele, a gente só vai ter que substituir o valor de e o valor de e calular o que restar. Como no nosso caso e , esse carinha fica
Aqui vale a gente lembrar que
Como nesse caso temos que é par, podemos escrever
Tudo bem até aí. Calculamos o primeiro carinha do nosso cofator.
Agora vamos para o cara mais estranho ainda, o . Este termo é o determinante da matriz que sobrar quando eliminarmos a linha e a coluna da nossa matriz inicial.
Vamos fazer isso para o nosso exemplo que vai ficar mais claro. Olhando a nossa matriz inicial e olhando a matriz que eu marquei a primeira linha e a terceira coluna:

Vemos que se elimarmos a linha que está marcada e a coluna que também está marcada, nos sobra 4 números (1,2,-1,4) que podemos escrever na seguinte matriz:
Essa matriz que sobrou é a nossa matriz . Shooow!
Agora, o que temos que calcular é o determinante dessa matriz nova que encontramos:
E aqui chegamos em um determinante de uma matriz onde podemos usar a regra de Sarrus: Marcamos as diagonais principal e secundária:

Fazemos o produto entre os elementos da diagonal principal (flecha azul):
Realizamos o produto entre os elementos da diagonal secundária (flecha vermelha) sem esquecer que temos que trocar o sinal desse produto:
Onde usamos que menos vezes menos dá mais!
Bom, agora temos os valores para calcular o determinante dessa matriz . Pela regra de Sarrus, vamos ter que somar esses produtos que calculamos agora:
Beleza!! Agora vamos juntar todos nossos resultados para calcular o cofator. Pela fórmula do cofator, podemos escrever:
Usando todos os resultados que obtemos:
E é assim que calculamos os cofatores!!
Show de bola! Agora podemos usar esses carinhas para conhecer esse tal teorema de Laplace.
Teorema de Laplace
Temos tudo em mãos para podermos falar sobre esse teorema que vai nos ajudar muito. Vamos calcular o determinante dessa matriz aqui:
Ficou assustudado? Confia no tio Laplace que vai dar tudo certo!
Vamos lá!!
O primeiro passo que devemos tomar é escolher alguma das colunas. Você pode escolher qualquer uma à seu gosto mas a melhor opção é escolher a coluna que contenha mais zeros! Vocês já vão entender o porquê.
A coluna que tem mais zero é a quarta coluna. Ela tem dois zeros ali: um na primeira linha e um na última. Beleza, então já escolhemos a nossa coluna!
Agora eu vou te mostrar a fórmula do teorema de Laplace, vai parecer um pouco estranha mas vamos conhecer cada um dos seus elementos. Se escolhemos a coluna 4, o teorema de Laplace nos fala que:
Nessa fórmula, aqueles termos são os elementos da nossa matriz. Por exemplo, o é o elemento que está na linha 1 e na coluna 4 que é o número 0. O é o elemento que está na linha 2 e na coluna 4 que é o número 1. O é o elemento que está na linha 3 e na coluna 4 e é o número 3. Por fim, o é o elemento que está na linha 4 e na coluna 4 e é o número 0.
Percebeu que todos os elementos na fórmula do determinante estão na coluna 4? A razão disso é que a gente escolheu essa coluna lá no começo. A fórmula sempre vai estar relacionada com a coluna que escolhermos, ok? A fórmula geral para qualquer coluna que a gente escolher é essa daqui:
Muito bem, voltando para nossa fórmula para a coluna que escolhemos (coluna 4), já que conhecemos todos os elementos que aparecem nela, podemos substituir na fórmula
Mesmo sem eu ter te falado quem são esses triangulinhos que estão aparecendo aí, já podemos realizar esses produtos por estes números que eu adicionei aíE aqui vemos a razão de escolhermos a coluna que possui mais zeros. Os zeros que aparecem na coluna reduzem o número de termos que vamos ter que calcular no determinantes. Entendeu a malandragem?
Muito bem, esses que aparecem aí são os cofatores que a gente conheceu agora há pouco!! Vamos para cima deles agora.
Calculando os cofatores
Por conta daqueles zeros que apareceram, nossa tarefa se reduziu a calcular só dois cofatores: o e o . Usando a fórmula do cálculo dos cofatores, podemos escreverUsando o resultado de para ímpar ou par, obtemos
Calculando determinantes de matrizes menores menores
Beleza!! Agora precisamos calcular esses determinantes das matrizes que sobrarem quando fizermos as eliminações das linhas e colunas. Vamos começar com o .
Para calcular o , primeiro marcamos a segunda linha e quarta coluna da nossa matriz A:

Dessa maneira, os números que não foram marcados, na ordem em que estão aparecendo, formam a nossa matriz
Agora precisamos calcular seu determinante! Por se tratar de uma matriz , devemos repetir as suas duas primeiras colunas e escrever:
Agora traçamos as diagonais para baixo e para cima:

Somando todos os produtos de todas as diagonais azuis (flechas para baixo):
Agora, somamos os produtos de todas as diagonais laranjas (flechas para cima):
Não podemos esquecer que para as flechas para cima, temos que trocar o sinal deste último resultado, então ficamos com:
Por fim, para calcular o determinante da matriz , devemos somar os resultados para as flechas para baixo com o resultado para as flechas para cima:
Opa! Já calculamos o primeiro determinante. Guarda esse resultado aí no bolso pois vamos precisar dele no final.
Vamos calcular o determinante da matriz . Para isso, precisamos escrever nossa matriz eliminando a terceira linha e quarta coluna da nossa matriz inicial :

Dessa maneira, os números que não foram marcados, na ordem em que estão aparecendo, formam a nossa matriz
Agora precisamos calcular seu determinante! Por se tratar de uma matriz , devemos repetir as suas duas primeiras colunas e escrever:
Agora traçamos as diagonais para baixo e para cima:
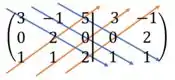
Somando todos os produtos de todas as diagonais azuis (flechas para baixo):
Agora, somamos os produtos de todas as diagonais laranjas (flechas para cima):
Não podemos esquecer que para as flechas para cima, temos que trocar o sinal deste último resultado, então ficamos com:
Por fim, pela regra de Sarrus, para calcular o determinante da matriz , devemos somar os resultados para as flechas para baixo com o resultado para as flechas para cima:
Opaa!! Conseguimos os dois determinantes que queríamos! Com isso, nossos cofatores ficam:
Agora é só devolver esses cofatores na nossa fórmula do teorema de Laplace:
Shoooow!!!
Viu como conseguimos calcular esse determinante usando o teorema de Laplace? Eu vou escrever o passo a passo aqui para você levar para a vida pois o processo vai ser sempre esse quando formos calcular determinantes de matrizes maiores que :
- Escolher a coluna que contenha o maior número de zeros;
- Escrever a fórmula do teorema de Laplace para a coluna escolhida:
- Substituir os elementos da coluna escolhida na fórmula do teorema de Laplace;
- Calcular os cofatores que restaram (aqui você vai se deparar com outros determinantes para você calcular, mas as matrizes vão ser menores e você vai conseguir usar a Regra de Sarrus na maioria das vezes😊);
- Substituir os valores na fórmula do teorema de Laplace.
Se você seguir esse passo é só sucesso!!!
Bom, agora, para você ficar craque no teorema de Laplace, é hora de praticar!!
Estarei de esperando lá 😊
Teorema de Laplace
Calculando os cofatores
Calculando determinantes de matrizes menores menores
Exercícios Resolvidos
Exercício Resolvido #1
Apostila Álgebra Linear - UNICAMP
Considerando a matriz
Ache o cofator do elemento
Passo 1
Faaaala galerinhaa !! Prontos para começar mais uma seção?!
Bom pessoal, o teorema de Laplace vai nos ajudar a achar o determinante quando as matrizes são muito grandes e sua determinação pelo jeito normal seria bem complicado, certo?
Agora galerinha, vamos aprender outro conceito muito importante?
O cofator do elemento é calculado usando uma fórmula bem Tranquilinha:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
O termo elevado ao número ímpar, resulta , ok?
Esse carinha é o que a gente chama de menor complementar. Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul (aqui eu já multipliquei todo mundo por pois vamos precisar desse carinha com um menos na frente logo logo):

E o determinante é o valor da direita (vermelho) menos o da esquerda (azul).:
Então, como a gente encontrou lá em cima que :
E assim achamos o cofator !!
Resposta
Exercício Resolvido #2
Apostila Álgebra Linear - UNICAMP
Considerando a matriz
Ache o menor complementar do elemento
Passo 1
Para este exercício, vamos precisar ter bem fresco na cabeça o conceito de menor complementar !!
O menor complementar pode ser representado por , onde representa a linha em que ele se encontra e a sua coluna
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Quer saber de uma coisa? O determinante dessa matriz aí de cima é o que a gente chama de menor complementar! Vamos calcular ele. Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:
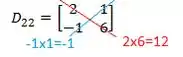
E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
E assim achamos o menor complementar !!
Resposta
Exercício Resolvido #3
Apostila Álgebra Linear - UFF
Considerando a matriz
Ache o cofator do elemento
Passo 1
Vamos seguir?
Já sabemos que o cofator do elemento é calculado usando uma fórmula bem tranquilinha:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
O termo elevado ao número par, resulta , ok?
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna
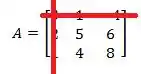
E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:
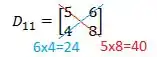
E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então, como a gente viu lá em cima que , temos:
E assim achamos o cofator !!
Resposta
Exercício Resolvido #4
Apostila Álgebra Linear - UFF
Considerando a matriz
Ache o cofator do elemento
Passo 1
Vamos seguir?
Já sabemos que o cofator do elemento é calculado usando uma fórmula bem tranquilinha:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
O termo elevado ao número ímpar, resulta , ok?
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna
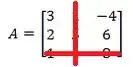
E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul (aqui eu já multipliquei todo mundo por pois vamos precisar desse carinha com um menos na frente logo logo):
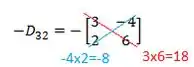
E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então, como :
E assim achamos o cofator !!
Resposta
Exercício Resolvido #5
Apostila Álgebra Linear - UFF
Encontre o determinante da matriz expandindo em cofatores ao longo da primeira linha:
Passo 1
Bora dificultar esse negócio? Hahahah ...
Brincadeira galerinha, vamos é facilitar!!
Para calcular um determinante usando o Teorema de Laplace vamos escolher uma linha ou coluna qualquer, de preferência a que tenha mais zeros, e usar a seguinte relação:
Usei aqui os elemento da primeira linha, porque o problema pediu isso, certo?
Agora vamos substituir?
Então, só precisamos achar os cofatores e , ok?
Já sabemos que o cofator do elemento é calculado usando essa formulinha aqui:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
Passo 2
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna
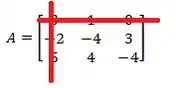
E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:

E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então:
E assim achamos um dos cofatores !!
Passo 3
Para o elemento nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:

E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então, como :
E agora vamos colocar no determinante?
Legal, não foi ?!
Resposta
Exercício Resolvido #6
Apostila Álgebra Linear - UFF
Encontre o determinante da matriz expandindo em cofatores ao longo da primeira coluna:
Passo 1
Na questão anterior achamos o determinante desta mesma matriz, mas usando a primeira linha, certo?
Agora nós vamos usar a coluna para vocês observarem como obtemos o mesmo valor, ok?! ver que vocês
Vamos dar uma olhada como ficaria este determinante?
Usei aqui os elemento da primeira coluna, porque o problema pediu isso, certo?
Agora vamos substituir?
Então, precisamos achar os cofatores , e , ok?
Já sabemos que o cofator do elemento é calculado usando uma fórmula bem tranquilinha:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
Passo 2
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna
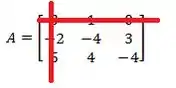
E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:

E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então:
E assim achamos um dos cofatores !!
Passo 3
Para o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
Para resolver o determinante multiplicamos os números presentes sobre a diagonal vermelha e azul (aqui eu já multipliquei todo mundo por pois vamos precisar desse carinha com um menos na frente logo logo):

E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então, como :
Passo 4
Para o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
Para resolver o determinante multiplicamos os números presentes sobre a diagonal vermelha e azul:

E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então:
E agora vamos colocar no determinante?
E chegamos à resposta final! Ebaaa!!
Deu um trabalhinho essa, né? Isso foi por que o exercício já mandava a gente escolher uma coluna ruim. Sempre é mais fácil escolher a coluna que tenha mais zeros!
Vamos para a próxima
Resposta
Exercício Resolvido #7
Apostila Álgebra Linear - UFABC
Seja
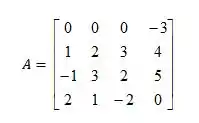
Encontre o determinante da matriz expandindo em cofatores.
Passo 1
Já sabemos como calcular os determinantes, certo?
Então o primeiro passo será escolher qual linha ou coluna vamos utilizar !! Vamos escolher aquela que possui mais zeros, para facilitar nossa vida, ok?
Olhando a cara dessa matriz aquela sequência de zeros na primeira linha é tentadora não é? Então vai ser essa linha mesma que a gente vai escolher!!
Vamos dar uma olhada como ficaria este determinante?

Agora vamos substituir?
Então, precisamos achar o cofator , ok? Viu que escolher aquela primeira linha reduziu muuuuito o nosso trabalho?
Já sabemos que o cofator do elemento é calculado usando uma fórmula bem tranquilinha:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
Passo 2
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna
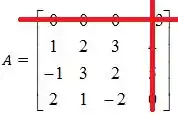
E com o que sobrou vamos montar um novo determinante (eu já estou colocando o sinal de menos ali na frente pois vai adiantar um pouco o nosso trabalho):
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso vamos adicionar ao lado dessa matriz a primeira e a segunda coluna:
Agora multiplicamos os números presentes sobre a diagonal vermelha e azul:
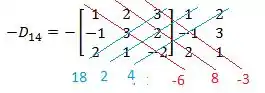
E para achar o determinante somamos os valores da direita (vermelho) e substraímos pela soma dos elementos da esquerda (azul):
Então:
Achando o determinante:
E assim achamos o determinante !!
Resposta
Exercício Resolvido #8
Apostila Álgebra Linear - UNICAMP
Seja
Encontre o determinante da matriz expandindo em cofatores.
Passo 1
Já sabemos como calcular os determinantes, certo?
Então o primeiro passo será escolher qual linha ou coluna vamos utilizar !! Vamos escolher aquela que possui mais zeros, para facilitar nossa vida, ok?
Vamos optar pela terceira linha? É um bom plano... tem dois zeros ali, acho que serve!
Vamos dar uma olhada como ficaria este determinante?

Agora vamos substituir?
Então, precisamos achar os cofatores e , ok?
Já sabemos que o cofator do elemento é calculado usando uma fórmula bem tranquilinha:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
Passo 2
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna
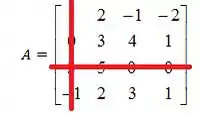
E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso vamos adicionar ao lado dessa matriz a primeira e a segunda coluna:
Agora multiplicamos os números presentes sobre a diagonal vermelha e azul:
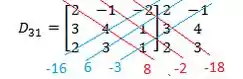
E para achar o determinante somamos os valores da direita (vermelho) e substraímos pela soma dos elementos da esquerda (azul):
Passo 3
Como o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante (aqui eu já multipliquei tudo por menos pois vai ajudar a gente mais para frente):
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso vamos adicionar ao lado dessa matriz a primeira e a segunda coluna:
Agora multiplicamos os números presentes sobre a diagonal vermelha e azul:

E para achar o determinante somamos os valores da direita (vermelho) e substraímos pela soma dos elementos da esquerda (azul):
Então, como :
Achando o determinante:
E assim achamos o determinante !!
Resposta
Exercício Resolvido #9
Apostila Álgebra Linear - UFF
Seja

Encontre o determinante da matriz expandindo em cofatores.
Passo 1
Já sabemos como calcular os determinantes, certo?
Então o primeiro passo será escolher qual linha ou coluna vamos utilizar !! Vamos escolher aquela que possui mais zeros, para facilitar nossa vida, ok?
Então, escolhemos a coluna , afinal, ela tem 3 zeros!!
Vamos dar uma olhada em como ficaria este determinante?

Agora vamos substituir?
Então, precisamos achar o cofator , ok?
Já sabemos que o cofator do elemento é calculado usando uma fórmula bem tranquilinha:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
Passo 2
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso vamos adicionar ao lado dessa matriz a primeira e a segunda coluna:
Agora multiplicamos os números presentes sobre a diagonal vermelha e azul:

E para achar o determinante somamos os valores da direita (vermelho) e substraímos pela soma dos elementos da esquerda (azul):
Então:
Achando o determinante:
E assim achamos a nossa resposta !!
Resposta
Exercício Resolvido #10
Apostila Álgebra Linear - UFF
Calcule o com uma expansão em cofatores ao longo de uma linha ou coluna de sua escolha.
Passo 1
Bom galerinha, podemos escolher qual linha ou coluna usar, então optamos pela menos trabalhosa !!
Que tal a coluna?
Vamos dar uma olhada como ficaria este determinante?
Agora vamos substituir?
Então, precisamos achar os cofatores , e , ok?
Já sabemos que o cofator do elemento é calculado usando uma fórmula meio chatinha, mas vamos fazer devagar:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
Agora precisamos lembrar de duas regrinha muito importante
- Número negativo elevado a expoente par fica positivo
- Número negativo elevado a expoente ímpar continua negativo
Então nossos cofatores ficarão
Passo 2
Para achar aqueles alí, que são chamados de menor complementar, vamos excluir a linha e a coluna do elemento, ok?
Para o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:
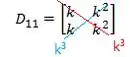
E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então:
E assim achamos um dos cofatores !!
Passo 3
Para achar nós cortamos a linha e a coluna
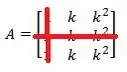
E com o que sobrou vamos montar um novo determinante (aqui eu já multipliquei todo mundo por pois vamos precisar desse valor negativo para calcular o ):
Já vimos que o determinante dessa mesma matriz ali em cima!
Então:
Passo 4
Para o elemento é nós cortamos a linha e a coluna
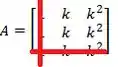
E com o que sobrou vamos montar um novo determinante:
Então:
E agora vamos colocar no determinante?
E assim a gente fecha mais uma!!