Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Combinação Linear

Ver Todos os Exercícios

Teoria

Faaala, Aí! Vamos aprender agora sobre um assunto que vai nos ajudar muito em alguns assuntos de espaços vetoriais. Vamos aprender sobre as combinações lineares!!

Introdução

A ideia da combinação linear é a seguinte. Se tivermos alguns vetores de um espaço vetorial, a gente consegue montar um outro vetor desse espaço a partir de uma combinação daqueles vetores que a gente já tinha. A gente faz uma combinação específica aqui que é a chamada combinação linear.

Então, vamos pegar um espaço vetorial qualquer V e escolhemos alguns vetores desse espaço. Por exemplo, escolhemos os vetores v 1 ,   v 2 e v 3 . Podemos montar um quarto vetor, w , com a ajuda de 3 números reais quaisquer a ,   b e c (a quantidade de números que vamos precisar tem a ver com o número de vetores que escolhemos) através da combinação linear a seguir:

w   = a . v 1 + b .   v 2 + c . v 3

É só isso mesmo. Vai ficar melhor de entender na prática!

Construindo vetores através da combinação linear

Vamos gerar um terceiro vetor que seja uma combinação linear dos vetores v 1 = ( 1,2 ) e v 2 = 2,2 !

Para isso, vamos precisar de dois números reais quaisquer (já que temos dois vetores para fazermos a combinação linear). Podemos escolher quaisquer valores, então eu vou escolher a = 1 e b = 2 . Usando a fórmula da combinação linear, teremos:

w   = a . v 1 + b .   v 2

Como só temos dois vetores, a gente elimina aquele terceiro vetor que aparecia na primeira fórmula que eu mostrei para vocês. Se tivéssemos quatro vetores, íamos precisar de mais um número real, d , e acrescentar um vetor v 4 no fim de tudo.

Substituindo os vetores que o problema nos passou e as constantes que a gente escolheu, temos:

w = 1 . 1,2 + 2 .   ( 2,2 )

Para calcularmos essa quantidade, precisamos primeiro multiplicar os vetores por aqueles números de fora ali. Fazemos isso multiplicando cada componente pelo número em questão:

w = 1 × 1 , 1 × 2 + 2 × 2 , 2 × 2 = 1,2 + 4,4

Agora somamos os números que estão na mesma posição naqueles parêntesis ali:

w = 1 + 4 ,   2 + 4 = ( 5,6 )

Viu só? A partir dos vetores v 1 = ( 1,2 ) e v 2 = 2,2 conseguimos construir um terceiro w = 5,6 através da combinação linear!

Combinação linear de Matrizes

Vamos ver como essa ideia funciona para o espaço vetorial das matrizes 2 × 2 , ou M 2 ( R ) .

Construa um terceiro vetor pela combinação linear dos vetores v 1 = 1 0 0 1 e v 2 = 0 1 0 0 .

Para fazermos isso, mais uma vez vamos precisar escolher dois números reais quaisquer à nossa escolha. Vamos usar os mesmo do exemplo anterior, a = 1 e b = 2 . Escrevendo a combinação linear:

w   = a . v 1 + b .   v 2

Agora, colocando nossos valores escolhidos nesta fórmula, temos

w = 1   . 1 0 0 1 + 2 . 0 1 0 0

Realizamos estes produtos multiplicando cada elemento das matrizes pelo número correspondente:

w = 1 × 1 1 × 0 1 × 0 1 × 1 + 2 × 0 2 × 1 2 × 0 2 × 0 w =   1 0 0 1 + 0 2 0 0

A soma de matrizes é dada somando cada elemento de uma matriz com o elemento na mesma posição da outra matriz. Então, ficamos com

w =   1 + 0 0 + 2 0 + 0 1 + 0 =   1 2 0 1

Show? Viu como a partir dos vetores v 1 = 1 0 0 1 e v 2 = 0 1 0 0 conseguimos escrever um terceiro vetor w =   1 2 0 1 que é uma combinação linear daqueles dois primeiros!

Um conceito que vai ser muuuito importante é sobre a dependência ou independência linear. É isso que vamos aprender agora 😊

Linearmente Independentes ou Linearmente Dependentes

Se tivermos um conjunto com um número qualquer de vetores { v 1 ,   v 2 ,   v 3 ,   … ,   v n } , esses vetores podem ser classificados em dois tipos:

  • Linearmente Dependentes ou L.D.
  • Linearmente Independentes ou L.I.

Essa classificação é importante pois pode facilitar muito alguns problemas que vamos ter de resolver, ok?

Muito bem, mas o que eu quero dizer com LD ou LI? Bom, o conjunto vai ser dito linearmente dependentes quando pelo menos um daqueles vetores do conjunto for combinação linear de outros vetores do conjunto. Se nenhum dos vetores for combinação linear de outros vetores do conjunto, dizemos que o conjunto é linearmente independentes.

A gente vai entender melhor isso na prática!

Olha só esse conjunto de vetores aqui:

1,1 ,   2,2 ,   0,1

Quando nos deparamos com um conjunto de vetores e queremos ver se é LD ou LI, a pergunta que devemos sempre nos fazer é a seguinte: Será que algum desses vetores eu consigo escrever em termos de algum outro vetor?

Se a resposta desta pergunta for positiva, de cara o conjunto é LD. Caso contrário, é LI.

Para respondermos isso, temos algumas técnicas. Eu vou ensinar as principais e uma delas vai valer sempre!

A primeira tentativa é no olho mesmo. A gente tem que olhar os vetores e vamos ver se a gente consegue ver alguma relação entre eles. Hummm. Olha o segundo vetor e o primeiro: 1,1 ; 2,2

Concorda comigo que o segundo é o dobro do primeiro?

2,2 = 2 × 1,1

Opa!! Se isso acontece, o segundo vetor é uma combinação linear do primeiro vetor... Então, nosso conjunto é linearmente dependente!!

Essa maneira de olharmos o conjunto funciona bem quando temos um vetor sendo múltiplo do outro ou dois vetores somados que dão o terceiro. Fora disso, fica um pouco mais difícil fazer assim. Então, se você tentou só olhar e identificar o conjunto e não conseguiu, não tem problema, você vai pular para a próxima técnica que eu vou ensinar agora 😊

Vamos classificar o seguinte conjunto em L.D ou L.I.

2,1 , 1 ; 1,2 , 1 ; 1,1 , 2

Aqui, olhar e procurar quais vetores são combinações dos outros vai ser uma tarefa um pouco demorada. Então, o jeito que a gente usa é escrever esses vetores em uma matriz. Sim, é isso mesmo que você ouviu, esses parêntesis a gente consegue representar em uma matriz que cada uma das linhas da matriz é um desses vetores. Assim, ó:

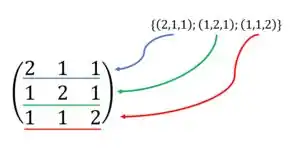
Então, a matriz para verificar se esse conjunto é LD ou LI é:

2 1 1 1 2 1 1 1 2

Feito isso, a gente vai ter que escalonar essa matriz. Se não lembra, não tem problema, vamos fazer isso juntos aqui. Bom, a gente tem que ter uma matriz que tenha elementos diferente de zero apenas na diagonal principal e acima dela. Para simplificar (isso vai diminuir um pouco a nossa tarefa), nossa primeira operação elementar vai ser a troca de linhas:

L 1 ↔ L 3

Dessa maneira, ficamos com:

1 1 2 1 2 1 2 1 1

Agora precisamos zerar todos os elementos abaixo daquele númeor 1 na primeira linha e primeira coluna. Fazemos isso zerando o 1 da segunda linha e o 2 da terceira linha com as seguintes operações:

L 2 ← L 2 - L 1

L 3 ← L 3 - 2 L 1 Ficamos então com:

1 1 2 1 - 1 2 - 1 1 - 2 2 - 2.1 1 - 2.1 1 - 2.2

Realizando os produtos primeiro:

1 1 2 1 - 1 2 - 1 1 - 2 2 - 2 1 - 2 1 - 4

Calculando as subtrações, ficamos com

1 1 2 0 1 - 1 0 - 1 - 3

Bom, agora vamos para a segunda linha. Nosso primeiro elemento diferente de zero, que é o 1, deve ter somente zeros abaixo dele e aquele - 1 está ali para nos atrapalhar ☹

Vamos sumir com aquele - 1 fazendo a seguinte operação:

L 3 ← L 3 + L 2

Dessa forma

1 1 2 0 1 - 1 0 + 0 - 1 + 1 - 3 + ( - 1 ) =   1 1 2 0 1 - 1 0 + 0 - 1 + 1 - 3 - 1

Realizando as somas da terceira linha temos:

1 1 2 0 1 - 1 0 0 - 4

Opa!! Chegamos à forma escalonada da nossa matriz!!!

Tá, e o que a gente faz com isso? Bom, aqui está a resposta do nosso problema:

  • Se a forma escalonada da matriz que carrega os vetores do conjunto não possuir nenhuma linha nula (com todos os números iguais a zero), o conjunto é dito linearmente independente;
  • Se a forma escalonada da matriz dos vetores do conjunto possuir pelo menos uma linha nula, o conjunto é dito linearmente dependente.

Como a nossa matriz escalonada não possui nenhuma linha nula, o conjunto dado é linearmente independente, ou seja, nenhum daqueles vetores pode ser escrito como combinação linear dos outros vetores do conjunto!

Showw? Então é isso, galera. A gente agora fica com a tarefa de praticar bastante esse tópico para ficarmos fera, combinado?

Estarei esperando vocês lá nos exercícios 😊

Combinação linear de Matrizes

Linearmente Independentes ou Linearmente Dependentes

Exercícios Resolvidos

Exercício Resolvido #1

Teste de conhecimento – álgebra linear - UNIT

Qual dos vetores abaixo é uma combinação linear do vetor v = 3,3 , 6 ?

  1. 1,2 , 3
  2. 3,2 , 4
  3. 4,4 , 3
  4. 1,1 , 2
  5. ( 2,4 , 6 )

Passo 1

Faaaala aí!! Vamos começar com os exercícios sobre combinação linear 😊

Bom o enunciado pede pra gente um vetor que seja combinação linear de

v = 3,3 , 6

Bom pra gente ter uma combinação linear a gente precisa que o vetor que queremos achar seja uma operação entre um ou mais vetores.

No caso dessa questão, como só temos um vetor, só podemos trabalhar com multiplicação, então quando multiplicamos por um escalar todos os números tem que estar certinhos!

Vamos analisar um pouquinho esse vetor v , a gente tem 3 ,   3   e depois 6 . E a gente consegue ver um padrãozinho desse vetor que é repetir o primeiro

Passo 2

Então temos que achar um vetor que repete o primeiro valor!

Com isso, já ficamos só com duas opções possíveis

c) 4,4 , 3

d) ( 1,1 , 2 )

Passo 3

Show, agora temos que analisar um pouco mais nosso vetorzinho. Já vimos nosso padrão, agora vamos mexer um pouco com ele!

Além da repetição, a gente consegue ver que temos um padrão que depois de repetir, temos um múltiplo, se liga:

Vamos colocar 3 em evidência:

v = 3 ⋅ 1,1 , 2

Olha só quem apareceu!!

d) 1,1 , 2

Assim a gente vê que

1,1 , 2 = 1 3 . v

O que caracteriza uma combinação linear do vetor que o exercício nos deu!!

Resposta

d) 1,1 , 2

Exercício Resolvido #2

Álgebra Linear 4 – teste de conhecimento combinação linear – Estácio

Qual dos vetores abaixo é uma combinação linear do vetor v = 1,2 , - 3 ?

  1. U = ( 3,10 , - 15 )
  2. U = - 3,8 , 9
  3. U = ( - 2 , - 4,6 )
  4. U = ( 4,8 , - 9 )
  5. U = ( - 1,2 , 3 )

Passo 1

Faaaala aí! Bora para mais uma questão sobre combinação linear? Simbora então!

Bom pra gente ter uma combinação linear a gente precisa que o vetor que queremos achar seja uma operação entre um ou mais vetores.

No caso dessa questão, como só temos um vetor, só podemos trabalhar com multiplicação, então quando multiplicamos por um escalar todos os números tem que estar certinhos!

Então vamos começar com a primeira opção:

v = 1,2 , - 3

E

U = 3,10 , - 15

Vendo pela primeira coordenada de cada vetor, vemos que temos que multiplicar v por 3

3 v = 3 ⋅ 1,2 , - 3

3 v = 3,6 , - 9

Opa, bateu no primeiro, mas os outros números não são iguais, logo 3 v ≠ U . Então não é essa ☹

Passo 2

Vamos para segunda!

v = 1,2 , - 3

E

U = - 3,8 , 9

Para chegarmos na primeira coordenada, temos que multiplicar v por - 3

- 3 v = - 3 ⋅ 1,2 , - 3

- 3 v = - 3 , - 6,9

Bateu só no primeiro também né? Então também não é essa

Passo 3

Simbora para terceira!

v = 1,2 , - 3

E

U = - 2 , - 4,6

Comparando as primeiras coordenadas, precisamos multiplicar por - 2

- 2 v = - 2 ⋅ 1,2 , - 3

- 2 v = - 2 , - 4,6

Epa epa epa, deu - 2 v = U então U é múltiplo de v , logo o vetor é uma combinação linear de v

Resposta

c) ( - 2 , - 4,6 )

Exercício Resolvido #3

Lista 7 – Lista de exercícios Preceptoria – Álgebra – UEM

Verifique se no espaço vetorial R 2 o vetor v = ( 2 , - 4 ) é combinação linear de v 1 = ( 1,1 ) e v 2 = ( 1 , - 1 )

Passo 1

Faaaaaala aí! Simbora para uma questãozinha de combinação linear!

Combinação linear é a representação de um vetor (na nossa questão v ) a partir de operações com outros vetores ( na nossa questão   v 1 e v 2 )

Então vamos lá, temos que fazer operação com v 1 e v 2 para chegarmos em v , fazendo multiplicações e somas, vamos escrever desse jeitinho aqui

a 1 ⋅ v 1 + a 2 ⋅ v 2 = v

E vamos ver se isso é possível ou não

Passo 2

Substituindo o vetor u , v e w   na expressão do passo 1, temos

a 1 1,1 + a 2 1 , - 1 = ( 2 , - 4 )

Fazendo a distributiva, ficamos com

a 1 , a 1 + a 2 , - a 2 = 2 , - 4

Somando os vetores, ficamos com

a 1 + a 2 , a 1 - a 2 = ( 2 , - 4 )

O que vamos fazer é igualar os valores que estão “na mesma virgula” desse jeitinho aqui

a 1 + a 2 = 2 a 1 - a 2 = - 4

Passo 3

Belezinha, bora botar a mão na massa nesse sisteminha então!

a 1 + a 2 = 2 a 1 - a 2 = - 4

Vamos somar essas duas linhas

a 1 + a 2 + a 1 - a 2 = 2 - 4

2 a 1 = - 2

a 1 = - 2 2

a 1 = - 1

Passo 4

Show de bola, achamos a 1 , para acharmos a 2 vamos substituir em uma das linhas, a primeira linha parece ser mais tranquilinho, então vamos nela mesmo

a 1 + a 2 = 2

Substituindo, temos que

- 1 + a 2 = 2

a 2 = 2 + 1

a 2 = 3

Show de bolinhas , achamos dois valores de a 1 e a 2   então v é C.L de v 1 e v 2 ! Sendo que a 1 = - 1 e a 2 = 3

Resposta

v é C.L de v 1 e v 2 ! Sendo que a 1 = - 1 e a 2 = 3

Exercício Resolvido #4

Lista de exercícios de álgebra linear – PUC CAMPINAS

Sejam u = 2 , - 3,2 e v = - 1,2 , 4 . Escrever, se possível w = ( 7 , - 11,2 ) como combinação linear de u e v

Passo 1

Opa, e aí! Vamos para uma questãozinha de combinação linear!

Combinação linear é a representação de um vetor (na nossa questão w ) a partir de operações com outros vetores ( na nossa questão   u e v )

Então vamos lá, temos que fazer operação com u e v para chegarmos em w , fazendo multiplicações e somas, vamos escrever desse jeitinho aqui

a 1 ⋅ u + a 2 ⋅ v = w

E vamos ver se isso é possível ou não. Se não for possível, a gente vai ter a 1 = a 2 = 0 , beleza? Vamos lá!!

Passo 2

Substituindo o vetor u , v e w   na expressão do passo 1, temos

a 1 2 , - 3,2 + a 2 - 1,2 , 4 = 7 , - 11,2

Fazendo a distributiva, ficamos com

2 a 1 , - 3 a 1 , 2 a 1 + - a 2 + 2 a 2 + 4 a 2 = 7 , - 11,2

Somando os vetores, ficamos com

2 a 1 - a 2 , - 3 a 1 + 2 a 2 , 2 a 1 + 4 a 2 = ( 7 , - 11,2 )

O que vamos fazer é igualar os valores que estão “na mesma virgula” desse jeitinho aqui

2 a 1 - a 2 = 7 - 3 a 1 + 2 a 2 = - 11 2 a 1 + 4 a 2 = 2

Passo 3

Show, vamos partir pra cima desse sisteminha então!

2 a 1 - a 2 = 7 - 3 a 1 + 2 a 2 = - 11 2 a 1 + 4 a 2 = 2

Vamos dar uma olhada só nas duas primeiras linhas, e vamos começar multiplicando a primeira linha por dois!

4 a 1 - 2 a 2 = 14 - 3 a 1 + 2 a 2 = - 11

Agora vamos somar essas duas linhas!

( 4 a 1 - 2 a 2 ) + - 3 a 1 + 2 a 2 = 14 - 11

Fazendo essas somas, temos que

a 1 = 3

Passo 4

Uhul, achamos a 1 agora para acharmos a 2 , vamos escolher uma linha e substituir o valor de a 1 , vamos usar a última linha que a gente deixou de lado pra ela não se sentir inútil ahah

2 a 1 + 4 a 2 = 2

2 3 + 4 a 2 = 2

6 + 4 a 2 = 2

4 a 2 = 2 - 6

4 a 2 = - 4

Dividindo os dois lados por 4 , temos que:

a 2 = - 1

Uhul, achamos os valores de a 1 e a 2   e os dois são diferentes de zero! Então w é C.L de u e v ! Sendo que a 1 = 3 e a 2 = - 1

Resposta

w é C.L de u e v ! Sendo que a 1 = 3 e a 2 = - 1

Exercício Resolvido #5

Lista de exercícios de álgebra linear – PUC CAMPINAS

Verificar para cada caso, se o vetor w é combinação linear dos vetores u e v

u = 1 , - 2,1 ,   v = 2,1 , - 1 ,   w = ( 7,1 , - 2 )

Passo 1

Faaaaaaaaaaala aí, tudo certinho? Vamos para uma questãozinha de combinação linear!

Combinação linear é a representação de um vetor (na nossa questão w ) a partir de operações com outros vetores ( na nossa questão   u e v )

Então vamos lá, temos que fazer operação com u e v para chegarmos em w , fazendo multiplicações e somas, vamos escrever desse jeitinho aqui

a 1 ⋅ u + a 2 ⋅ v = w

E vamos ver se isso é possível ou não

Passo 2

Substituindo o vetor u , v e w   na expressão do passo 1, temos

a 1 1 , - 2,1 + a 2 2,1 , - 1 = 7,1 , - 2

Fazendo a distributiva, ficamos com

a 1 , - 2 a 1 , a 1 + 2 a 2 , a 2 , - a 2 = 7,1 , - 2

Somando os vetores, ficamos com

a 1 + 2 a 2 , - 2 a 1 + a 2 , a 1 - a 2 = 7,1 , - 2

O que vamos fazer é igualar os valores que estão “na mesma virgula” desse jeitinho aqui

a 1 + 2 a 2 = 7 - 2 a 1 + a 2 = 1 a 1 - a 2 = - 2

Passo 3

Show, vamos partir pra cima desse sisteminha então!

a 1 + 2 a 2 = 7 - 2 a 1 + a 2 = 1 a 1 - a 2 = - 2

Vamos dar uma olhada só nas duas últimas linhas, e vamos começar somando essas duas linhas

- 2 a 1 + a 2 + a 1 - a 2 = 1 - 2

- a 1 = - 1

a 1 = 1

Passo 4

Uhul, achamos a 1 agora para acharmos a 2 , vamos escolher uma linha e substituir o valor de a 1 , vamos usar a última linha também porque ela é mais bonitinha heeh

a 1 - a 2 = - 2

Substituindo o valor de a 1 , temos que:

1 - a 2 = - 2

- a 2 = - 2 - 1

- a 2 = - 3

a 2 = 3

Uhul, achamos dois valores de a 1 e a 2   então w é C.L de u e v ! Sendo que a 1 = 1 e a 2 = 3

Resposta

w é C.L de u e v ! Sendo que a 1 = 1 e a 2 = 3

Exercício Resolvido #6

Álgebra linear 3 – teste de conhecimento Combinação Linear - Estácio

Determine o valor de a para que o vetor u = ( - 1 , a , - 7 ) seja combinação linear dos vetores de S = { 1 , - 3,2 , 2,4 , - 1 }

  1. a = 15
  2. a = 17
  3. a = 16
  4. a = 13
  5. a = 14

Passo 1

Faaala galerinha, vamo que vamo para mais uma questão sobre combinação linear!

A gente quer que o vetor u seja combinação linear de dois vetores, vamos dar nome aos bois para ficar mais bonitinho

w = 1 , - 3,2

v = 2,4 , - 1

Então vamos lá, temos que fazer operação com w e v para chegarmos em u , fazendo multiplicações e somas, vamos escrever desse jeitinho aqui

a 1 ⋅ w + a 2 ⋅ v = u

E queremos o valor de a dentro do vetor u

Passo 2

Vamos ver aqui como fica substituindo os vetores pelos seus valores!

a 1 1 , - 3,2 + a 2 2,4 , - 1 = - 1 , a , - 7

Fazendo a distributiva, ficamos com

a 1 , - 3 a 1 , 2 a 1 + 2 a 2 , 4 a 2 , - a 2 = - 1 , a , - 7

Somando os vetores, ficamos com

a 1 + 2 a 2 , - 3 a 1 + 4 a 2 , 2 a 1 - a 2 = - 1 , a , - 7

O que vamos fazer é igualar os valores que estão “na mesma virgula” desse jeitinho aqui

a 1 + 2 a 2 = - 1 - 3 a 1 + 4 a 2 = a 2 a 1 - a 2 = - 7

Passo 3

Vamos por enquanto esquecer essa segunda linha, depois a gente se preocupa com esse a , agora vamos focar em a 1   e a 2

a 1 + 2 a 2 = - 1 2 a 1 - a 2 = - 7

Simbora multiplicar a linha de baixo por 2

a 1 + 2 a 2 = - 1 4 a 1 - 2 a 2 = - 14

Somando as duas linhas, temos

5 a 1 = - 15

a 1 = - 3

Passo 4

Show agora bora achar a 2 , vamos escolher uma dessas duas linhas para substituir o valor que achamos de a 1 , vamos com a primeira linha que parece mais fácil

a 1 + 2 a 2 = - 1

Substituindo a 1 por - 3 , temos:

- 3 + 2 a 2 = - 1

2 a 2 = - 1 + 3

2 a 2 = 2

a 2 = 1

Passo 5

Showdi, agora vamos olhar para linha do meio, temos que

- 3 a 1 + 4 a 2 = a

Substituindo os valores de a 1 e a 2 , ficamos com

- 3 - 3 + 4 1 = a

9 + 4 = a

a = 13

Resposta

d) a = 13

Exercício Resolvido #7

Lista 7 – Lista de exercícios Preceptoria – Álgebra – UEM

Determine o valor de k para que o vetor v = 1 , - 2 , k   ϵ   R 3 seja combinação linear dos vetores v 1 = ( 3,0 , - 2 ) e v 2 = ( 2 , - 1 , - 5 )

Passo 1

Faaaaaaaaaala aí! Vamos para mais um exercício sobre combinação linear! Uhul

Combinação linear é a representação de um vetor (na nossa questão v ) a partir de operações com outros vetores ( na nossa questão   v 1 e v 2 ) .

Então vamos lá, temos que fazer operação com v 1 e v 2 para chegarmos em v , fazendo multiplicações e somas, vamos escrever desse jeitinho aqui

a 1 ⋅ v 1 + a 2 ⋅ v 2 = v

E queremos o valor de k dentro do vetor v

Passo 2

Vamos ver aqui como fica substituindo os vetores pelos seus valores!

a 1 3 , 0 , - 2 + a 2 2 , - 1 , - 5 = 1 , - 2 , k

Fazendo a distributiva, ficamos com

3 a 1 , 0 , - 2 a 1 + 2 a 2 , - a 2 , - 5 a 2 = 1 , - 2 , k

Somando os vetores, ficamos com

3 a 1 + 2 a 2 , 0 - a 2 , - 2 a 1 - 5 a 2 = 1 , - 2 , k

Ajeitando um pouquinho, temos:

3 a 1 + 2 a 2 , - a 2 , - 2 a 1 - 5 a 2 = 1 , - 2 , k

O que vamos fazer é igualar os valores que estão “na mesma virgula” desse jeitinho aqui

3 a 1 + 2 a 2 = 1 - a 2 = - 2 - 2 a 1 - 5 a 2 = k

Passo 3

Belezinha, vambora para esse sisteminha, vamos ignorar um pouquinho essa última linha, primeiro vamos nos preocupar com a 1 e a 2 e depois vamos ver esse k , então o nosso sisteminha fica

3 a 1 + 2 a 2 = 1 - a 2 = - 2

Opa, essa segunda linha já dá a dica pra gente

- a 2 = - 2           →           a 2 = 2

Agora vamos pegar esse valor e colocar na primeira linha para acharmos a 1

3 a 1 + 2 ⋅ 2 = 1

3 a 1 + 4 = 1

3 a 1 = 1 - 4

3 a 1 = - 3

a 1 = - 1

Passo 4

Opa, show de bola achamos a 1 e a 2 para encontrarmos k !!

Temos na última linha que:

- 2 a 1 - 5 a 2 = k

Vamos substituir os valores que encontramos no passo anterior

- 2 - 1 - 5 2 = k

k = 2 - 10

k = - 8

Resposta

k = - 8

Exercício Resolvido #8

Lista de exercícios de álgebra linear – PUC CAMPINAS

Sejam u = 2 , - 3,2 e v = - 1,2 , 4 . Para qual valor de k ,   w = ( - 8,14 , k ) é combinação linear de u e v ?

Passo 1

Faaaala aí! Vamos para cima de mais uma questãozinha de combinação linear!

Combinação linear é a representação de um vetor (na nossa questão w ) a partir de operações com outros vetores ( na nossa questão   u e v ) .

Então vamos lá, temos que fazer operação com u e v para chegarmos em w , fazendo multiplicações e somas, vamos escrever desse jeitinho aqui

a 1 ⋅ u + a 2 ⋅ v = w

E queremos o valor de k dentro do vetor w

Passo 2

Vamos ver aqui como fica substituindo os vetores pelos seus valores!

a 1 2 , - 3,2 + a 2 - 1,2 , 4 = - 8,14 , k

Fazendo a distributiva, ficamos com

2 a 1 , - 3 a 1 , 2 a 1 + - a 2 , 2 a 2 , 4 a 2 = - 8,14 , k

Somando os vetores, ficamos com

2 a 1 - a 2 , - 3 a 1 + 2 a 2 , 2 a 1 + 4 a 2 = - 8,14 , k

O que vamos fazer é igualar os valores que estão “na mesma virgula” desse jeitinho aqui

2 a 1 - a 2 = - 8 - 3 a 1 + 2 a 2 = 14 2 a 1 + 4 a 2 = k

Passo 3

Show, vamos partir pra cima desse sisteminha então!

2 a 1 - a 2 = - 8 - 3 a 1 + 2 a 2 = 14 2 a 1 + 4 a 2 = k

Vamos dar uma olhada só nas duas primeiras linhas, e vamos começar multiplicando a primeira linha por dois!

4 a 1 - 2 a 2 = - 16 - 3 a 1 + 2 a 2 = 14

Agora vamos somar essas duas linhas!

4 a 1 - 2 a 2 + - 3 a 1 + 2 a 2 = - 16 + 14

Fazendo essas somas, temos que

a 1 = - 2

Passo 4

Agora para acharmos a 2 vamos substituir o valor de a 1 em alguma linha (a primeira que parece mais fácil)

2 a 1 - a 2 = - 8

2 - 2 - a 2 = - 8

- 4 - a 2 = - 8

Vamos multiplicar os dois lados por - 1 pra ficar mais bonitinho

4 + a 2 = 8

a 2 = 4

Passo 5

Show de bolinhas, achamos a 1 e a 2 mas a gente quer achar o valor de k , temos na última linha do nosso sisteminha isso daqui:

2 a 1 + 4 a 2 = k

A gente achou a 1 e a 2 então é só substituir e partir para o abraço!

2 - 2 + 4 4 = k

- 4 + 16 = k

k = 12

Resposta

k = 12

Exercício Resolvido #9

Lista 7 – Espaço e Subespaço Vetorial – UEM

Determinar os escalares, p , q , r   ϵ   R tal que possamos escrever o vetor v = 1,2 , 3   ϵ   R 3 como

1,2 , 3 = p ⋅ 1,0 , 0 + q ⋅ 1,1 , 0 + r ⋅ ( 1,1 , 1 )

Passo 1

Oieee! Vamo que vamo para mais uma questão sobre Combinação Linear!

O enunciado já deu pra gente como a gente vai fazer essa combinação, que é desse jeitinho aqui:

p ⋅ 1,0 , 0 + q ⋅ 1,1 , 0 + r ⋅ 1,1 , 1 = 1,2 , 3

Vamos começar fazendo a distributiva

p , 0,0 + q , q , 0 + r , r , r = ( 1,2 , 3 )

Passo 2

Shoow de bola, agora vamos somar os vetores, ficando com:

p + q + r , 0 + q + r , 0 + 0 + r = 1,2 , 3

Ajeitando isso daí ficamos com

p + r + q , r + q , r = ( 1,2 , 3 )

O que vamos fazer é igualar os valores que estão “na mesma virgula” desse jeitinho aqui

p + r + q = 1 r + q = 2 r = 3

Opa, a última linha já dá a ideia pra gente!

r = 3

Passo 3

Na segunda linha temos que

r + q = 2

Substituindo o valor que encontramos de r

3 + q = 2

q = 2 - 3

Logo

q = - 1

Passo 4

Agora que temos r e q , vamos para a primeira linha do nosso sisteminha, substituir esses valores e achar a última variável

p + q + r = 1

Substituindo pelos valores que encontramos, temos que

p + - 1 + 3 = 1

p - 1 + 3 = 1

p + 2 = 1

Passando esse - 2 para o outro lado, temos:

p = 1 - 2

p = - 1

Uhuul, achamos os valores das 3 variáveis

Resposta

p = - 1 ,   q = - 1 e r = 3

Exercício Resolvido #10

Lista Subespaço Vetorial e Combinação Linear – PUC CAMPINAS

Verificar se o vetor z = ( 2,1 , 2 ) é combinação linear de u = 3,2 , 1 ,   v = 1,0 , 1 e w = ( 3,1 , 0 ) .

Passo 1

Faaaala aí! Vamos para cima de mais uma questãozinha de combinação linear!

Combinação linear é a representação de um vetor (na nossa questão z ) a partir de operações com outros vetores ( na nossa questão   u ,   v e w ) .

Então vamos lá, temos que fazer operação com u , v e w para chegarmos em z , fazendo multiplicações e somas, vamos escrever desse jeitinho aqui

a 1 ⋅ u + a 2 ⋅ v + a 3 ⋅ w = z

Passo 2

Vamos ver aqui como fica substituindo os vetores pelos seus valores!

a 1 3,2 , 1 + a 2 1,0 , 1 + a 3 ( 3,1 , 0 ) = 2,1 , 2

Fazendo a distributiva, ficamos com

3 a 1 + 2 a 1 + a 1 + a 2 + 0 + a 2 + ( 3 a 3 , a 3 , 0 ) = 2,1 , 2

Somando os vetores, ficamos com

3 a 1 + a 2 + 0,2 a 1 + 0 + a 3 , a 1 + a 2 + 0 = ( 2,1 , 2 )

O que vamos fazer é igualar os valores que estão “na mesma virgula” desse jeitinho aqui

3 a 1 + a 2 + 3 a 3 = 2 2 a 1 + a 3 = 1 a 1 + a 2 = 2

Passo 3

Vamos partir pra cima desse sisteminha!

3 a 1 + a 2 + 3 a 3 = 2 2 a 1 + a 3 = 1 a 1 + a 2 = 2

A primeira coisa que a gente vai fazer é, pegar essa última linha e jogar o a 1 para o outro lado, ficando com isso daqui:

a 2 = 2 - a 1

Vamos pegar isso e colocar nas duas linhas de cima!

3 a 1 + 2 - a 1 + 3 a 3 = 2 2 a 1 + a 3 = 1

Vamos ajeitar essa primeira linha que está bem feinha!

2 a 1 + 3 a 3 = 0 2 a 1 + a 3 = 1

Bora subtrair essas linhas para achar a 3

2 a 1 + 3 a 3 - ( 2 a 1 + a 3 ) = 0 - 1

Ajeitando isso daí, temos

2 a 3 = - 1

a 3 = - 1 2

Passo 4

Show, achamos a 3 , agora vamos ver quanto vale a 1 a partir disso!

Temos, pela segunda linha que

2 a 1 + a 3 = 1

2 a 1 - 1 2 = 1

Passando esse - 1 2 para o outro lado, temos:

2 a 1 = 1 + 1 2

2 a 1 = 2 2 + 1 2

2 a 1 = 3 2

a 1 = 3 2 ⋅ 1 2

Isso dá pra gente

a 1 = 3 4

Passo 5

Só falta nosso a 2 ! Para isso vamos usar a última linha do nosso sisteminha

a 1 + a 2 = 2

3 4 + a 2 = 2

a 2 = 2 - 3 4

a 2 = 8 4 - 3 4

Isso dá pra gente que

a 2 = 5 4

Show, então z é C.L. de u , v e w com a 1 = 3 4 , a 2 = 5 4 e a 3 = - 1 2

Resposta

z é C.L. de u , v e w com a 1 = 3 4 , a 2 = 5 4 e a 3 = - 1 2