Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Transformação Linear

Ver Todos os Exercícios

Teoria

Fala aí! Bora aprender de uma vez por todas como provar que uma transformação é linear?!

O que é uma Transformação Linear?

Dizemos que uma transformação é uma função que tem um conjunto chamado de domínio, um conjunto chamado de contradomínio e uma fórmula de associação, que de alguma forma consegue levar os valores de para .

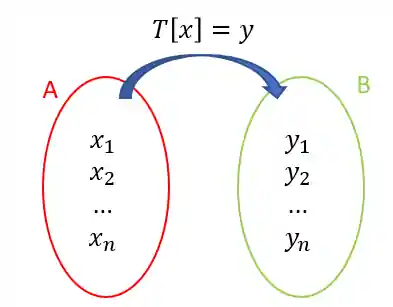
Transformação
Transformação

Ou seja, quando falamos sobre transformação linear estamos falando de uma função, que é capaz de alterar o valor de um resultado de acordo com um determinado valor de entrada (input).

Por exemplo a função , tem todos os números reais em seu domínio, e sempre tem como resultado outros números reais, então podemos escrever que:

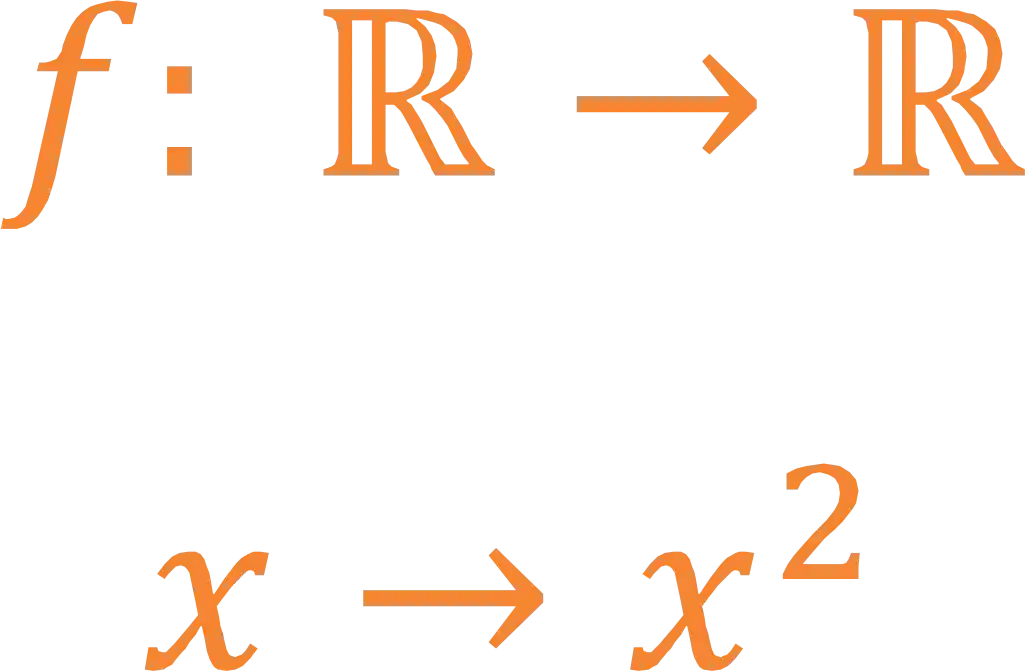
Domínio da função f(x)
Domínio da função f(x)

Podemos pensar em uma maquininha que recebe um número (ou um vetor) e cospe um outro número (ou outro vetor). A transformação é a responsável por fazer a ligação entre o domínio e o contradomínio.

Ou seja, enquanto com as funções estamos acostumados com transformações apenas entre dois números reais, quando falamos de transformações lineares estamos falando de funções que admitem qualquer espaço vetorial como argumento e como saída.

Então vamos ver um exemplo de uma transformação:

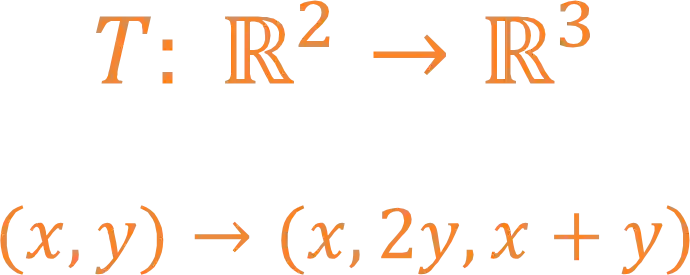
Exemplo de transformação linear
Exemplo de transformação linear

Nesse caso ao escolher dois valores, um para e um para , definimos um ponto de 3 coordenadas no . A transformação é exatamente a expressão que nos gera essa mudança.

📢 Clique para saber mais:

Como saber se é uma transformação linear?

E o que significa dizer que uma transformação é linear? Uma transformação é dita linear quando obedece aos seguintes critérios:

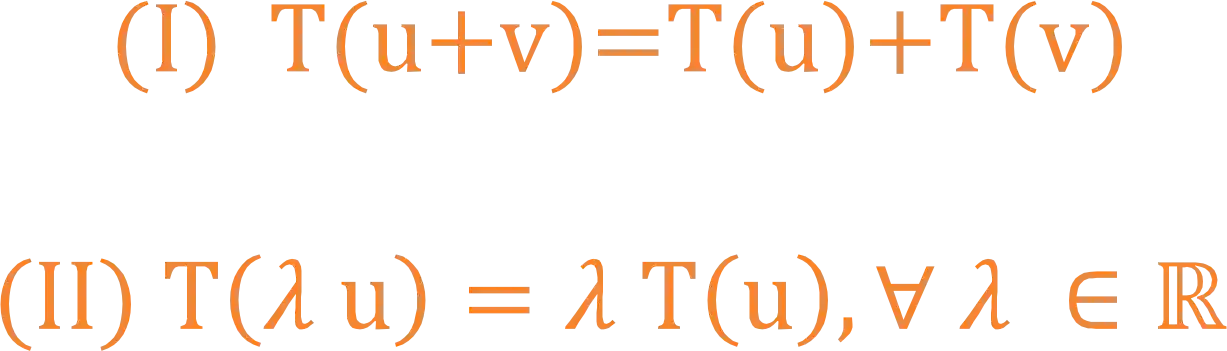
Condições pra uma transformação ser linear
Condições pra uma transformação ser linear

Se o domínio e o contradomínio de transformação linear (TL) forem espaços do mesmo tipo, chamamos a transformação de Operador Linear.

UFA!, QUANTA COISA! Agora que já entendemos o que são transformações e já sabemos a regra que temos que verificar para saber se são lineares ou não, chegou a hora de aprender como podemos provar que uma transformação é linear ou não.

Pra isso, confere esse vídeo iradoso que o Responde Aí preparou pra você! 👇

Exemplo: Verifique se a transformação a seguir é linear

Vamos usar a transformação que já discutimos um pouco logo a cima:

Passo 1: Verificar a se a primeira condição é válida

Para isso vamos precisar desenvolver os dois lados da equação e verificar se eles coincidem.

Passo 2: Desenvolver o lado esquerdo (I)

Logo o lado vale:

Passo 3: Desenvolver o lado direito (II)

Expandindo, encontramos que o lado vale:

Passo 4: Comparar o lado (I) com o lado (II)

Dessa forma chegamos a conclusão que:

E portanto essa transformação satisfaz a primeira condição para ser uma transformação linear, vamos agora verificar se ela também satisfaz a segunda condição.

Passo 5: Verificar a segunda condição

Precisamos verificar, se:

Passo 6: Desenvolver o lado esquerdo (III)

Passo 7: Desenvolver o lado direito (IV)

Desenvolvendo o lado direito :

Passo 8: Comparar os lados (III) e (IV)

Logo como podemos observar:

E portanto essa transformação também satisfaz a segunda condição para ser considerada linear.

Passo 9: Conclusão

Podemos concluir então que é uma transformação linear.

Agora vamos praticar com mais exercícios?

Exemplo: Verifique se a transformação a seguir é linear

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 126 – Fix 4.1.

Determine se são transformações lineares T : R 2 → R 2 :

a   T x , y = ( x + 2 y , x y )

b   T x , y = ( x + 2 y , 0 )

c   T x , y = ( x 2 + 2 y , y )

Passo 1

Nesse exercício basta verificarmos se as transformações respeitam as condições para serem uma T L . Lembram quais são?

1   T u + v = T u + T v

2   T λ u = λ T u ,   ∀   λ ∈ R

Vamos começar então ;)

Passo 2

a I   T x 1 , y 1 + T x 2 , y 2 =   T x 1 + x 2 , y 1 + y 2   I I

Desenvolvendo o lado I :

T x 1 , y 1 + T x 2 , y 2

x 1 + 2 y 1 ,   x 1 y 1 + x 2 + 2 y 2 ,   x 2 y 2

x 1 + 2 y 1 + x 2 + 2 y 2 , x 1 y 1 + x 2 y 2

Desenvolvendo o lado I I :

T x 1 + x 2 , y 1 + y 2

  x 1 + x 2 + 2 y 1 + y 2 ,   x 1 + x 2 y 1 + y 2

Passo 3

Igualando I a I I :

x 1 + 2 y 1 + x 2 + 2 y 2 , x 1 y 1 + x 2 y 2 = x 1 + x 2 + 2 y 1 + y 2 ,   x 1 + x 2 y 1 + y 2

Dessa igualdade, chegamos ao seguinte:

x 1 + 2 y 1 + x 2 + 2 y 2 = x 1 + x 2 + 2 y 1 + y 2 x 1 y 1 + x 2 y 2 = x 1 + x 2 y 1 + y 2

Podemos ver que a primeira equação é satisfeita, mas a segunda claramente não bate. Logo, a transformação da letra a não é linear.

Passo 4

b I   T x 1 , y 1 + T x 2 , y 2 =   T x 1 + x 2 , y 1 + y 2   I I

Desenvolvendo o lado I :

T x 1 , y 1 + T x 2 , y 2

x 1 + 2 y 1 ,   0 + x 2 + 2 y 2 ,   0

x 1 + 2 y 1 + x 2 + 2 y 2 , 0

Desenvolvendo o lado I I :

T x 1 + x 2 , y 1 + y 2

  x 1 + x 2 + 2 y 1 + y 2 ,   0

Passo 5

Igualando I a I I :

x 1 + 2 y 1 + x 2 + 2 y 2 , 0 = x 1 + x 2 + 2 y 1 + y 2 ,   0

Daí,

x 1 + 2 y 1 + x 2 + 2 y 2 = x 1 + x 2 + 2 y 1 + y 2 0 = 0

Tanto a igualdade de cima quanto a de baixo conferem! Então ela é linear? Não!! Temos que verificar a segunda condição antes de podermos afirmar algo.

Passo 6

I I I   T λ x , λ y = λ T x , y   I V

Desenvolvendo o lado I I I :

T λ x , λ y

λ x + 2 λ y , 0

Desenvolvendo o lado I V :

λ T x , y

λ x + 2 y , 0

( λ x + λ 2 y , 0 )

Passo 7

Assim, podemos ver que I I I = ( I V ) .

Portanto, provamos que as condições da linearidade satisfazem a nossa transformação! Logo, podemos ver que ela é linear.

Passo 8

c I   T x 1 , y 1 + T x 2 , y 2 =   T x 1 + x 2 , y 1 + y 2   I I

Desenvolvendo o lado I :

T x 1 , y 1 + T x 2 , y 2

x 1 2 + 2 y 1 ,   y 1 + x 2 2 + 2 y 2 ,   y 2

x 1 2 + 2 y 1 + x 2 2 + 2 y 2 , y 1 + y 2

Desenvolvendo o lado I I :

T x 1 + x 2 , y 1 + y 2

x 1 + x 2 2 + 2 y 1 + y 2 , y 1 + y 2

Passo 9

Igualando I a I I :

x 1 2 + 2 y 1 + x 2 2 + 2 y 2 , y 1 + y 2 = x 1 + x 2 2 + 2 y 1 + y 2 , y 1 + y 2

Logo, chegamos às igualdades:

x 1 2 + 2 y 1 + x 2 2 + 2 y 2 = x 1 + x 2 2 + 2 y 1 + y 2 y 1 + y 2 = y 1 + y 2

Já falhou na primeira igualdade, logo, não é uma transformação linear.

Resposta

a Não é linear.

b É linear.

c Não é linear.

Exercício Resolvido #2

Lista 1 para a p2, Questão 2-c), 2015.1, PUC-RIO.

Verifique se F é linear:

F p x = x 2 .   p ( x + 1 )

F : P 2 → P 4

Passo 1

Para vermos se F é linear, temos que verificar as duas condições:

1 ) F p 1 + p 2 x = F p 1 x + F ( p 2 ) ( x )

2 )   F λ p x = λ F ( p ) ( x )

Lembre-se que como o domínio é P 2 , estamos trabalhando com POLINÔMIOS! Isso quer dizer que estamos trabalhando com seus coeficientes e não sua variável x .

Vamos definir algumas coisas antes:

p 1 x = c 1 + b 1 x + a 1 x 2

p 2 x = c 2 + b 2 x + a 2 x 2

p 1 + p 2 x = c 1 + c 2 + b 1 + b 2 x + a 1 + a 2 x 2

F p x = x 2 c + b x + 1 + a x + 1 2

Passo 2

Vamos provar a primeira condição:

I     F p 1 + p 2 x = F p 1 x + F p 2 x     ( I I )

Vou desenvolver o lado ( I I ) :

F p 1 x + F p 2 x

= x 2 a 1 x + 1 2 + b 1 x + 1 + c 1 + x 2 a 2 x + 1 2 + b 2 x + 1 + c 2

= x 2 a 1 x + 1 2 + b 1 x + 1 + c 1 + a 2 x + 1 2 + b 2 x + 1 + c 2

= x 2 ( c 1 + c 2 + b 1 + b 2 ( x + 1 ) + a 1 + a 2 ( x + 1 ) 2 )

Podemos ver que isso é exatamente:

x 2 p 1 + p 2 x + 1

= F ( p 1 + p 2 ) ( x )

Assim, a condição 1 está provada.

Passo 3

Agora vamos desenvolver a condição 2:

F λ p x = x 2 λ p x + 1 = λ x 2 p x + 1 = λ ( x 2 p x + 1 ⏟ F ( p x ) )

= λ F ( p x )

Como provamos as duas condições, vemos que a transformação é linear.

Resposta

Sim, é linear.

Exercício Resolvido #3

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 219. - 38

Seja o espaço vetorial V = M 2 × 2 e a transformação linear:

T : V → R 3 ,

T a b c d = ( a + b , c - d , 2 a )

Mostre que T é linear.

Passo 1

Bom, pra uma transformação ser linear, como já sabemos, tem que satisfazer as condições:

1   T u + v = T u + T v

2   T λ u = λ T u ,   ∀   λ ∈ R

O próprio enunciado já afirma que ela é linear, mas nos pede pra mostrarmos isso. Logo, temos que testar ambas as condições e mostrar que, de fato, elas são atendidas.

Passo 2

Vamos provar a primeira condição:

I   T a 1 b 1 c 1 d 1 + T a 2 b 2 c 2 d 2 =   T a 1 + a 2 b 1 + b 2 c 1 + c 2 d 1 + d 2   I I

Desenvolvendo I :

T a 1 b 1 c 1 d 1 + T a 2 b 2 c 2 d 2

a 1 + b 1 , c 1 - d 1 , 2 a 1 + ( a 2 + b 2 , c 2 - d 2 , 2 a 2 )

a 1 + b 1 + a 2 + b 2 , c 1 - d 1 + c 2 - d 2 , 2 a 1 + 2 a 2

Agora o lado I I :

T a 1 + a 2 b 1 + b 2 c 1 + c 2 d 1 + d 2

a 1 + a 2 + b 1 + b 2 , c 1 + c 2 - d 1 - d 2 , 2 a 1 + a 2

Passo 3

Igualando I e I I :

a 1 + b 1 + a 2 + b 2 = a 1 + a 2 + b 1 + b 2 c 1 + c 2 - d 1 - d 2 = c 1 - d 1 + c 2 - d 2 2 a 1 + 2 a 2 = 2 a 1 + a 2

Todas as igualdades tão certinhas, então a transformação passou no primeiro teste. Vamos para a segunda condição agora!

Passo 4

I I I   T λ a λ b λ c λ d = λ T a b c d   I V

Lado I I I :

( λ a + λ b , λ c - λ d , 2 λ a )

Lado I V :

λ ( a + b , c - d , 2 a )

( λ a + λ b , λ c - λ d , 2 λ a )

Passo 5

-

Igualando I I I e I V podemos ver que de fato são iguais. Como a transformação satisfez ambas as condições, ela é linear.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

Transformações Lineares e Teorema Núcleo-Imagem

À questão “Dado v = x 0 y 0 z 0 ∈ M 3 × 1 fixo, a transformação T : M 3 × 3 ⟶ M 3 × 1 dada por T A = A v é linear?”, Andrezinho respondeu da seguinte maneira:

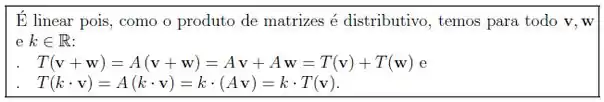
a) Embora T seja realmente uma transformação linear, a justificativa do Andrezinho não está correta. Qual foi o erro que ele cometeu?

b) Mostre que T é linear.

Passo 1

a Andrezinho errou a expressão da T L e também quem são os elementos do seu domínio. Assim, ele fez variar o vetor coluna v , w enquanto seu domínio é na verdade M 3 × 3 , ou seja quem deveria variar deveria ser uma matriz A ∈ M 3 × 3 e não um vetor coluna!

Assim, ele fixou matriz A , e tomou v , w como suas variáveis do problema, provando para uma S :   M 3 × 1 ⟶ M 3 × 1 dada por S v = A v e não uma T : M 3 × 3 ⟶ M 3 × 1 dada por T A = A v .

OBS: Talvez você tenha confundido que v , w ∈ R , também. Pois o jeito que ficou escrito, ficou meio confuso. Mas não tem problema pensar que v , w seriam números reais e não vetores colunas. Uma justificativa com esse argumento também é válida.

Passo 2

b Antes de começar, NÃO É NECESSÁRIO EXPANDIR A MATRIZ A COMO UMA 3 × 3 !! BASTA USAR AS PROPRIEDADES DAS MATRIZES!

Assim para provar que é linear basta fazermos:

  • T A 1 + A 2 = T A 1 + T ( A 2 )
  • T k A = k T A

Vamos provar essa primeiro:

I   T A 1 + A 2 = T A 1 + T A 2   ( I I )

Desenvolvendo o lado ( I I ) temos que:

T A 1 + T A 2 = A 1 v + A 2 v = A 1 + A 2 v = T A 1 + A 2

E assim vemos que I = ( I I ) !

Passo 3

Agora vamos provar que

I I I   T k A = k T A   ( I V )

Assim, vamos desenvolver o lado ( I I I ) :

T k A = k A v = k A v = k T ( A )

E assim podemos ver que os lados ( I I I ) e ( I V ) são iguais, E, portanto provamos as condições para nossa T ser linear!

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Uma transformação linear T:R ²→R ² ² ² de posto 2 transforma toda reta numa reta. Prove isto.
De um exemplo de uma transformação linear T sobrejetiva e não injetiva. Prove que é sobrejetiva e não injetiva.
Prove que uma transformação linear é injetiva se, e somente se, seu núcleo se reduz ao único elemento 0 ∈ R 3
Prove que, para toda transformação linear M : R 3 →R 3 , a transformação M * M é auto adjunta e que o núcleo de M * M coincide com o núcleo de M . Em particular, se M é invertível, o mesmo ocorre M *
Chama-se núcleo da transformação linear M : R 3 → R 3 ao conjunto N M = { v ∈ R 3 ; M v = 0 } . Determine os núcleos das transformações lineares dos exemplos 47.1 ,47.2 ,47.3e47.4 . prove que se u , v