Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1i
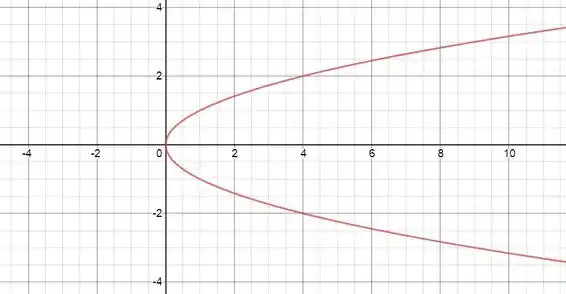
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.
Passo 1
Como temos uma das variáveis elevada ao quadrado e outra do primeiro grau, temos uma parábola! A parábola sempre fica “deitada” no eixo do termo do 1º grau. No nosso caso; no eixo . Colocando na forma canônica:
Como .
Passo 2
Esboçando essa parábola, ficamos com:
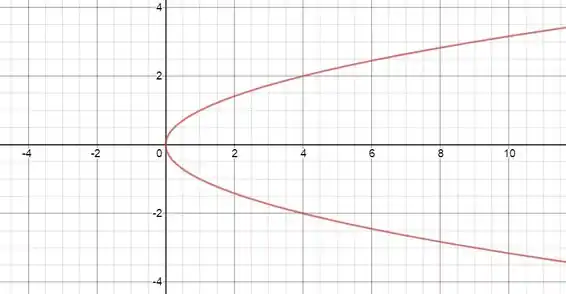
Passo 3
O seu foco é , ou seja:
Qualquer parábola tem excentricidade . É como se , o que também faz com que o nosso foco seja .
A diretriz da parábola é a reta
Resposta
Exercícios de Livros Relacionados
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 4 x 2 - 25 y 2 = 100
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 25 x 2 - 25 y 2 = 1
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 4 x 2 - y 2 - 8 x - 12 = 0
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 4 y 2 - 7 x 2 = 56
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 9 x 2 - 4 y 2 = 36