Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 5.6 - Ex. 30

Um espelho plano triangular é apoiado no canto de uma sala de forma descrita na figura abaixo.

Em que direção será refletido um feixe de luz de raios paralelos emitidos verticalmente de cima para baixo?

Passo 1

Galera, o importante aqui é prestar atenção na geometria da questão. O ângulo com que o raio bate no espelho é igualzinho ao que ele sai do espelho. Isso a gente sabe lá da física! Bom, se a gente reparar que o espelho tá bem simétrico no eixo e no eixo , dá pra gente imaginar mais ou menos qual vai ser a direção que o raio vem e que ele vai sair. Como a abscissa e a ordenada são iguais, o raio vai ser refletido num plano que forma com o eixo e com o eixo , bem na meiuca do espelho, dá pra visualizar?

Passo 2

Agora vamos trabalhar no plano em que ocorre a reflexão. O esboço da situação é mais ou menos assim:

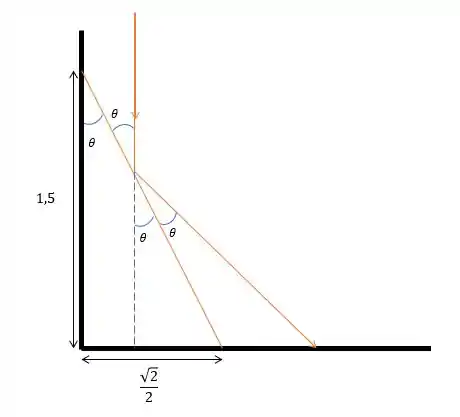
Esse vem do ângulo de que o plano forma ali com a base. Vamos calcular a tangente, o seno e o cosseno desse ângulo :

E aí, pra achar o seno, vamos substituir na relação fundamental da trigonometria:

E aí, nesse plano, como a gente pode ver do desenho, a direção dos raios vai ser de pra direita e pra baixo. Então vamos achar esses dois valores!

Passo 3

Beleza, já achamos a direção considerando esse plano! No eixo , a direção vai ser realmente a coordenada pra baixo, mas essa que está orientada com vai ter que ser decomposta em e . Como está a , vai ser moleza!

A direção, considerando a reflexão no , vai ser:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine quais das seguintes funções são aplicações lineares: f : R 2 → R 2 ( x , y ) → x + y , x - y g : R 2 → R ( x , y ) → x y h : M 2 → R a cb d → det ⁡ a cb d k : P 2 → P 3 a x 2 + b x + c → a x

Seja L : R 3 → R 3 onde L é a reflexão através do plano 3 x + 2 y + z = 0 .Encontre L ( x , y , z ) .Encontre uma base ordenada γ de R 3 , tal que T γ γ = 1 0 00 1 00 0 - 1

Sejam S e T aplicações lineares de V em W . Definimos S + T como S + T v = S v + T ( v ) para todo v ∈ V e definimos α S como α S v = α ⋅ S v para todo α ∈ R e v ∈ V .Mostre que S + T é uma transforma

Sejam α = 1 , - 1 , 0,2 e β = 1,0 , - 1 , 0,1 , 2 , 1,2 , 0 bases de R 2 e R 3 respectivamente e T β α = 1 1 00 1 - 1 .Ache T . Se S ( x , y ) = ( 2 y , x - y , x ) ache S β α .Ache uma base γ de R 3

Seja D : P 3 → P 3 f → f " ( d e r i v a d as e g u n d a ) Mostre que D é linear e determine uma base para ker ⁡ D .