Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 38b
Identifique a quádrica descrita pela equação dada.
(b)
Passo 1
Bom, vamos dar uma olhada nessa equação:
O nosso problema aqui é encontrar a equação reduzida.
Logo de cara aparece um problema: aparecem multiplicando um ao outro! Precisamos dar um jeito nisso.
A melhor forma de resolver esse tipo de problema é aplicando uma mudança de coordenadas.
Quando queremos nos livrar de termos do tipo , é melhor usar uma rotação de coordenadas.
Passo 2
Como o nosso problema só está nas variáveis e , vamos fazer uma rotação no plano , ou seja, em torno do eixo :
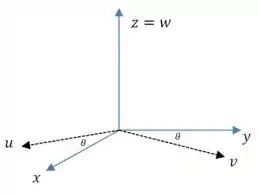
E vamos lembrar da matriz de rotação, que é uma forma fácil de lembrar como fica essa rotação.
No nosso caso, e são o resultado de uma rotação de e por um ângulo no sentido anti-horário:
Essa matriz faz justamente isso: rotacionar as coordenadas por um ângulo no sentido anti-horário.
Multiplicando aquelas matrizes, encontramos o seguinte:
Beleza, agora vamos substituir essas expressões de e na equação lá de cima:
Passo 3
Voltando na nossa equação:
Para simplificar, vamos começar olhando só para esses dois primeiros termos:
E vamos substituir com as expressões ali de cima:
E o termo misturando que causou problemas é:
Isso tudo também ia ficar muito confuso se a gente somar as três expressões. Então primeiro vamos ver quais termos sobram com o produto .
Nessas simplificações aí de cima, nós usamos essas identidades aqui:
Como a nossa expressão era:
Então, substituindo, esse termo aqui vai aparecer:
Se a gente quiser que o termo com suma, precisamos de:
E qual o ângulo que tem seno e cosseno com mesmo módulo e sinais opostos? É o , ou , então:
Passo 4
Beleza, com essa informação vamos voltar na equação original:
A gente já viu que os três primeiros termos (quando tudo que multiplica some) ficam assim:
E como :
E esse seno é:
Então:
Beleza, jogando isso no equação completa:
Simplificando um pouco:
E substituindo e de novo pelas coordenadas novas:
E colocando e em evidência:
E como a gente já definiu , todos esses termos nos parênteses são constantes!
Passo 5
Tá, pode parecer que está complicando de novo, mas olha só:
Já dá pra identificar qual é a equação!
Já sabemos que ele é uma quádrica cilíndrica, porque temos só duas variáveis e .
Como as duas variáveis estão elevadas ao quadrado, ela não pode ser parabólica, que é desse tipo aqui:
E também não pode ser hiperbólica, porque nesse caso as duas variáveis teriam sinais diferentes:
Então ela tem que ser uma quádrica elíptica:
Porque as duas variáveis tem sinais iguais! Assim como na nossa equação: as duas constantes que multiplicam e são positivas!
Resposta
A equação é uma quádrica cilíndrica elíptica.