Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.9 - Ex. 23a

A partir da Fórmula ( 15 ) , obtenha as matrizes canônicas das rotações em torno dos eixos x de R 3 .

Passo 1

Para começar temos que ter acesso a formula ( 15 ) que é:

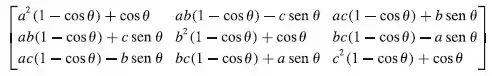
Sendo θ o ângulo de rotação do vetor:

p a r a   r o t a ç õ e s   n o   s e n t i d o   h o r á r i o   o   v a l o r   d e   θ   é   n e g a t i v o           p a r a   r o t a ç õ e s   n o   s e n t i d o   a n t i - h o r á r i o   o   v a l o r   d e   θ   é   p o s i t i v o

Passo 2

Agora vamos lembrar que durante a os vetores devem ser unitários, então façamos assim para um vetor v →   a ,   b ,   c :

R θ v x → = ( 1 ,   0 ,   0 )

Logo onde temos b e c   multiplicando qualquer termo o resultado será 0:

R θ v x → = 1 * 1 - cos θ + cos ⁡ θ 0 0 0 0 + cos ⁡ θ 0 + 1 * ( - sen ⁡ θ ) 0 0 + 1 * sen ⁡ θ 0 + cos ⁡ θ

Passo 3

Organizando a matriz e substituindo os valores obtemos:

R θ v x → = 1 0 0 0 cos ⁡ θ - sen ⁡ θ 0 sen ⁡ θ cos ⁡ θ

Resposta

R θ v x → = 1 0 0 0 cos ⁡ θ - sen ⁡ θ 0 sen ⁡ θ cos ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No exercício 2, em cada parte determine se A é uma matriz estocástica. Se A não for estocástica, explique por que não é. A = 1 / 12 1 / 9 1 / 6 1 / 2 0 5 / 6 5 / 12 8 / 9 0
No exercício 2, em cada parte determine se A é uma matriz estocástica. Se A não for estocástica, explique por que não é. A = - 1 1 / 3 1 / 2 0 1 / 3 1 / 2 2 1 / 3 0
No exercício 6, em cada parte, determine se P é uma matriz estocástica regular. P = 1 / 2 1 1 / 2 0
No exercício 2, em cada parte determine se A é uma matriz estocástica. Se A não for estocástica, explique por que não é. A = 0,2 0 , 8 0 , 9 0,1
No exercício 5, em cada parte, determine se P é uma matriz estocástica regular. P = 1 / 5 1 4 / 5 0