Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 41b

O ponto A é um dos vértices de um paralelepípedo e os três vértices adjacentes são B , C e D . Sendo A A ' uma diagonal do paralelepípedo, determinar o ponto A ' nos seguintes casos:

A - 1,2 , 1 , B 3 , - 1,2 , C 4,1 , - 3 e D 0 , - 3 , - 1

Passo 1

Primeiro vamos visualizar os pontos A , B , C , D e A ' , onde o ponto A é um dos vértices do paralelepípedo, os três vértices adjacentes são B , C e D , e A ' pertence a A A ' , que é uma diagonal do paralelepípedo:

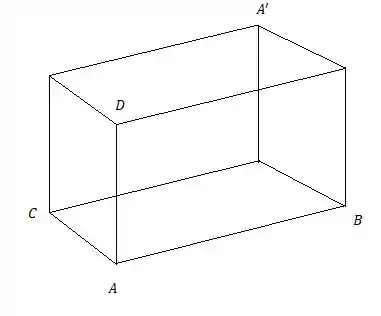
Vamos ver agora os vetores A B → , A C → , A D →   e A A ' → :

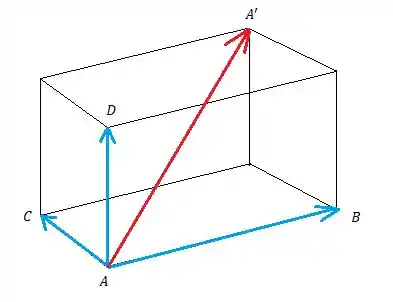
Passo 2

Podemos ver pela imagem acima que dá pra achar o ponto A ' através do vetor A A ' , vamos então mover os vetores A C → e A D → de forma que A C → = B E → e A D → = E A ' , assim vamos achar uma maneira de achar A A ' → :

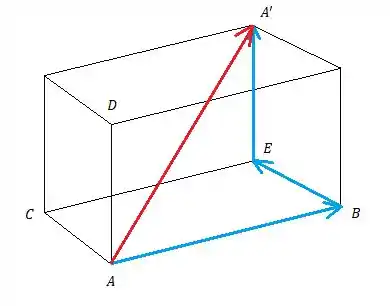
Agora dá pra ver que a diagonal pode ser calculada somando os vetores A B → , A C → e A D → , vamos calcular:

A A ' → = A B → + B E → + E A ' → = A B → + A C → + A D →

A B → = B - A = 3 , - 1,2 - - 1,2 , 1 = 3 - - 1 , - 1 - 2 , 2 - 1 = 4 , - 3 , 1

A C → = C - A = 4,1 , - 3 - - 1,2 , 1 = 4 - - 1 , 1 - 2 , - 3 - 1 = 5 , - 1 , - 4

A D → = D - A = 0 , - 3 , - 1 - - 1,2 , 1 = 0 - - 1 , - 3 - 2 , - 1 - 1 = 1 , - 5 , - 2

Passo 3

Vamos agora substituir:

A A ' → = A B → + A C → + A D → = 4 , - 3,1 + 5 , - 1 , - 4 + 1 , - 5 , - 2 =

= 4 + 5 + 1 , - 3 - 1 - 5 , 1 - 4 - 2 = 10 , - 9 , - 5

Agora vamos achar o ponto A ' :

A A ' → = A ' - A

A A ' → = 10 , - 9 , - 5 → A ' - A = 10 , - 9 , - 5 → A ' = 10 , - 9 , - 5 + A →

→ A ' = 10 , - 9 , - 5 + - 1,2 , 1 → A ' = 10 - 1 , - 9 + 2 , - 5 + 1 → A ' = 9 , - 7 , - 4

Pronto, temos então o ponto A ' = 9 , - 7 , - 4 .

Resposta

A ' = 9 , - 7 , - 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove que o segmento que une os pontos médios de dois lados de um triângulo é paralelo ao terceiro lado e tem comprimento igual à metade do comprimento desse lado.
Seja ABC um triângulo qualquer com medianas A D ̄ , B E ̄ e C F ̄ . Demonstre que A D→ +B E→ +C F →=0 → .
No paralelogramo ABCD ao lado, temos D E → = αD C → , 3 B F → = F C → e G é a interseção das retas A E ̄ e D F ̄ . Determine α para termos A G → = 4 G E → ;a seguir, expresse w → = C G → como combinaç
Sejam A, B, C e D quatro pontos e M e N os pontos médios dos segmentos AC e BD. Determine, em função de M N → , a soma s → = A B →+A D→ +C B →+C D → .(Sugestão: A B →=A M→ +M N →+N B → e, analogamente
Mostre que se α V = 0 - , então α = 0 ou V = 0 - .