Exercícios de Operações com Vetores - Lista de Exercícios Resolvida
Questão 1
Sabendo que e é o vetor que vai do ponto até o ponto
, determine o valor de para que
Ver solução completaQuestão 3
Sabendo que o ângulo entre os vetores e é de , determinar o ângulo formado pelos vetores:
- e
- e
- e
- e
Questão 8
Dados os vetores e da figura, mostrar, num gráfico, um representante do vetor:
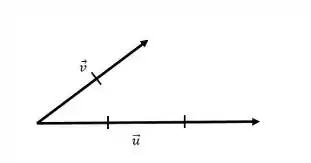
Questão 10
Seja um triângulo no espaço e sejam um ponto do segmento e um ponto do segmento tais que:
Se é o ponto na interseção dos segmentos e , então o quociente
é igual a:
- ;
- ;
- ;
- ;
- .
Questão 11
Na figura abaixo estão representados dois cubos unidos por uma face. Determine a soma dos vetores indicando um representante do resultado com os pontos da figura.
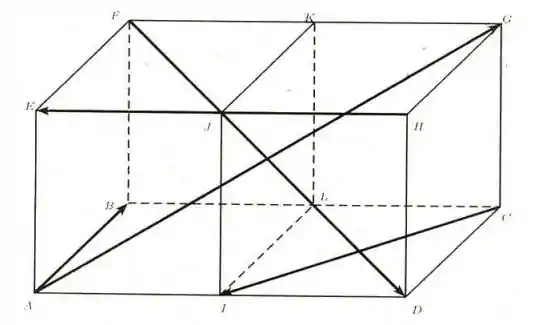
Questão 12
Considere, em , o triângulo de vértices . Seja o ponto sobre o lado tal que e seja o ponto no segmento tal que . Seja o ponto sobre o lado que está na reta que passa por e , conforme a figura (fora de escala):
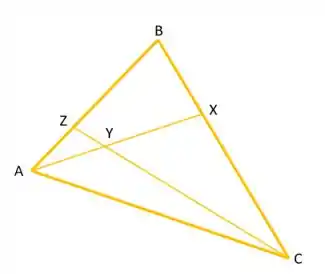
Se satisfaz , então é igual a
a)
b)
c)
d)
e)
f)
Ver solução completaQuestão 13
Considere uma base ortonormal de e sejam tais que o vetor seja uma combinação linear dos vetores . Suponha que , que seja ortogonal ao vetor e que o ângulo entre e o vetor seja agudo. Temos que é igual a:
Questão 14
Sejam u e v dois vetores do . Então:
(I)
(II) Se u for um múltiplo escalar de v (isto é, com a ∈ R) então
(a) Ambas as afirmações são falsas
(b) Ambas as afirmações são verdadeiras
(c) (I) é verdadeira e (II) é falsa
(d) (I) é falsa e (II) é verdadeira
Ver solução completaQuestão 16
Considere , e .
a) Determine um vetor paralelo a de comprimento igual a .
Ver solução completaQuestão 17
Dado um triângulo , sejam pontos sobre os lados , respectivamente, tais que . Então podemos afirmar que é igual a:
Ver solução completa
Questão 18
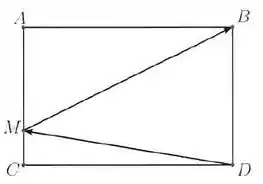
Considere a figura do retângulo abaixo. Sabendo que , escreva cada vetor a seguir como combinação linear de e .
a)
b)
Questão 19
Nesta questão, representa o produto misto de três vetores . Considere as seguintes afirmações para vetores de
Ver solução completa
Questão 20
Considere o tetraedro de vértices . Seja o ponto sobre a aresta tal que e seja o ponto sobre a aresta tal que . Se são tais que , então são iguais, respectivamente, a
Ver solução completaQuestão 21
Em , dado um triângulo de vértices sejam pontos sobre os lados , respectivamente, tais que . Então, é igual a
Ver solução completa