Mínimos Quadrados e Reflexões

Teoria

Como esperado, também podemos resolver problemas de reflexão usando o método dos Mínimos Quadrados. E a melhor parte é que usamos o resultado da projeção! Então não precisamos fazer contas extras. Devemos isso tudo ao lema abaixo:

Se multiplicarmos ambos os lados da igualdade pelo vetor que desejamos refletir teremos:

Toma um desenho pra ajudar a visualizar:

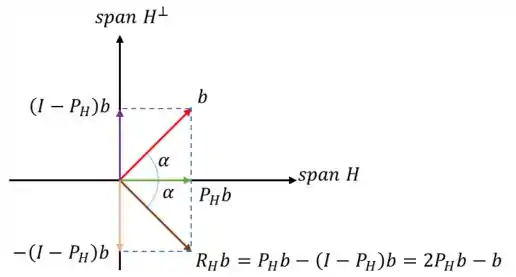
Então para acharmos a reflexão de em torno de , basta multiplicarmos a projeção de em por e subtrairmos de . Bem simples né? Vamos ver um exemplo:

Determine se e

Definimos e resolvemos:

Temos que , logo:

Obtendo a matriz Reflexão

Pelo lema que acabamos de ver temos que

Se multiplicarmos ambos os lados, como vimos, temos uma ferramenta poderosa para encontrarmos a reflexão de um vetor. Mas se mantivermos nessa forma, temos como obter a matriz reflexão diretamente da matriz projeção. Basta adaptarmos as fórmulas que vimos em projeção. Por exemplo, a reflexão em torno de um subespaço de dimensão gerado por um vetor :

Exemplo: Dê a matriz reflexão na reta do .

Blz, vamos achar o vetor gerador da reta pra botar na fórmula:

Obtendo a matriz Reflexão

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 164 – Ext 5.2 Adaptado

Determine as matrizes das :

reflexão em torno da reta

, reflexão em torno da reta

, reflexão em torno do plano

Passo 1

É pedida a matriz que representa a projeção sobre a reta . Primeiro vamos achar o vetor gerador da reta. Temos:

Logo os vetores da reta são da forma . Portanto, um vetor gerador possível é o

A fórmula da matriz projeção sobre a direção de um vetor é dada por:

Para acharmos a matriz rotação basta fazermos:

Passo 2

Agora precisamos da matriz que representa a projeção sobre a reta . Novamente, vamos achar o vetor que gera ela:

A fórmula da matriz projeção sobre a direção de um vetor é dada por:

Para acharmos a matriz rotação basta fazermos:

Passo 3

Queremos a reflexão em torno de um plano no . O que vamos fazer é o seguinte: Primeiro encontramos a matriz projeção no complemento ortogonal do plano. Com essa matriz em mãos encontramos a que faz a projeção no plano. Por fim, encontramos a matriz que reflete pelo plano.

Se não entendeu direito fica calmo que vai ficar claro no caminho haha. Primeiro, vamos encontrar o complemento ortogonal do plano.

Sabemos que ele é uma reta gerada por um vetor ortogonal ao plano. Este pode ser obtido pelos coeficientes da equação do plano:

A matriz que projeta sobre esta reta é dada por:

Passo 4

O próximo passo é encontrar que projeta o vetor sobre o plano. Ela é dada por:

Passo 5

Finalmente, podemos encontrar :

Resposta

Exercício Resolvido #2

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 163 – Prob 5.9

Sejam e . Calcule .